tree的遍历--广度优先遍历

一、定义

　　深度优先就是自上而下的遍历搜索，广度优先则是逐层遍历；

深度优先：

广度优先：

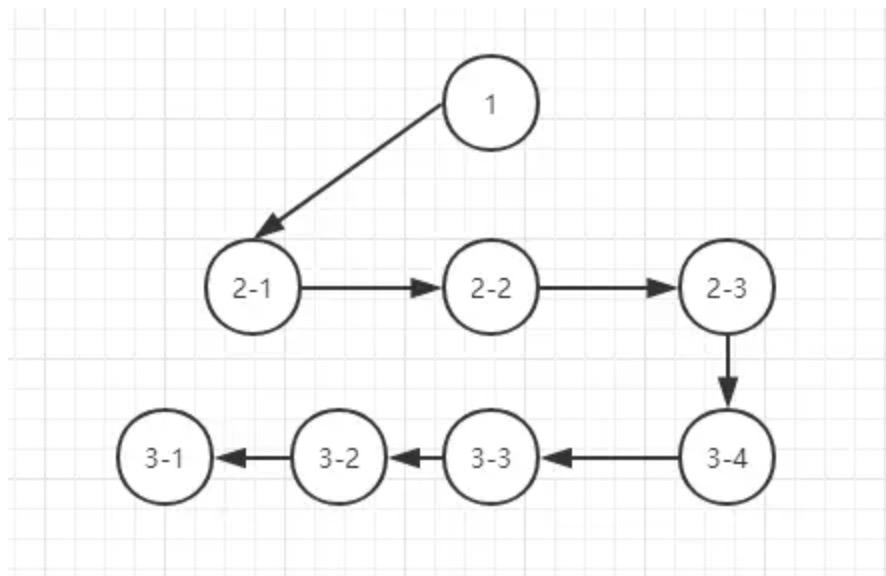
区别：

　　深度优先不需要记住所有的节点, 所以占用空间小, 而广度优先需要先记录所有的节点占用空间大

深度优先有回溯的操作(没有路走了需要回头)所以相对而言时间会长一点

深度优先采用的是堆栈的形式, 即先进后出
      广度优先则采用的是队列的形式, 即先进先出

二、demo

//html
<div id="root">
    <ul>
      <li class="li-1">
        <a href="">
          <img src="" alt="">
        </a>
      </li>
      <li class="li-2">
        <span></span>
      </li>
      <li class="li-3">
      </li>
    </ul>
    <p></p>
    <button></button>
 </div>

　　

深度优先：　　

//递归版本
  function deepFirstSearch(node, nodeList = []) {
    if (node) {
      nodeList.push(node);
      let children = node.children;
      for (let i = 0; i < children.length; i++) {
        //每次递归的时候将 需要遍历的节点 和 节点所存储的数组传下去
        deepFirstSearch(children[i], nodeList);
      }
    }
    return nodeList;
  }
  //非递归
  function deepFirstSearch2(node) {
    let nodes = []; //存放结果
    let stack = []; //栈
    if (node != null) {
      stack.push(node); //把当前的node推进stack中
      while (stack.length != 0) {
        let item = stack.pop();
        nodes.push(item);
        let children = item.children;

        for (let i = children.length - 1; i >= 0; i--) {
          stack.push(children[i]);
        }
      }
    }
    return nodes;
  }
  // console.log(deepFirstSearch2(node))

　　

广度优先：

  function breadFirstSearch(node) {
    let nodes = []; //结果
    let queue = []; //队列
    if (node) {
      queue.unshift(node);
      while (queue.length) {
        let item = queue.shift();
        nodes.push(item);
        let children = item.children;
        for (let i = 0; i < children.length; i++) {
          queue.push(children[i]);
        }
      }
    }
    return nodes;
  }

  console.log(breadFirstSearch(node));

　　

三、数据和树结构相互转换

树结构转化为扁平化数组主要采用上面所说的深度优先遍历和广度优先遍历，那么数组结构转化为树结构主要是：

非递归：

/**
 * 数组转树  非递归求解
 * 利用数组和对象相互引用  时间复杂度O(n)
 * @param {Object} list
 */
function toTree(list,parId) {
    let obj = {};
    let result = [];
    //将数组中数据转为键值对结构 (这里的数组和obj会相互引用)
    list.map(el => {
        obj[el.id] = el;
    })
    for(let i=0, len = list.length; i < len; i++) {
        let id = list[i].parentId;
        if(id == parId) {
            result.push(list[i]);
            continue;
        }
        if(obj[id].children) {
            obj[id].children.push(list[i]);
        } else {
            obj[id].children = [list[i]];
        }
    }
    return result;
}

let res1 = toTree(arr,0)

　　

递归：

/**
 * 数组转树  递归求解
 */
function toTree(list,parId){
	let len = list.length
	function loop(parId){
		let res = [];
		for(let i = 0; i < len; i++){
			let item = list[i]
			if(item.parentId === parId){
				item.children = loop(item.id)
				res.push(item)
			}
		}
		return res
	}
	return loop(parId)
}

let result = toTree(arr,0)