圆方树简介（UOJ30：CF Round #278 Tourists）

我写这篇博客的原因

证明我也是学过圆方树的

顺便存存代码

---

前置技能

双联通分量：点双

然后就没辣

圆方树

建立

新建一个图

定义原图中的所有点为圆点

对于每个点双联通分量(只有两个点的也算)

建立一个方点，向所有的点双内的点连边

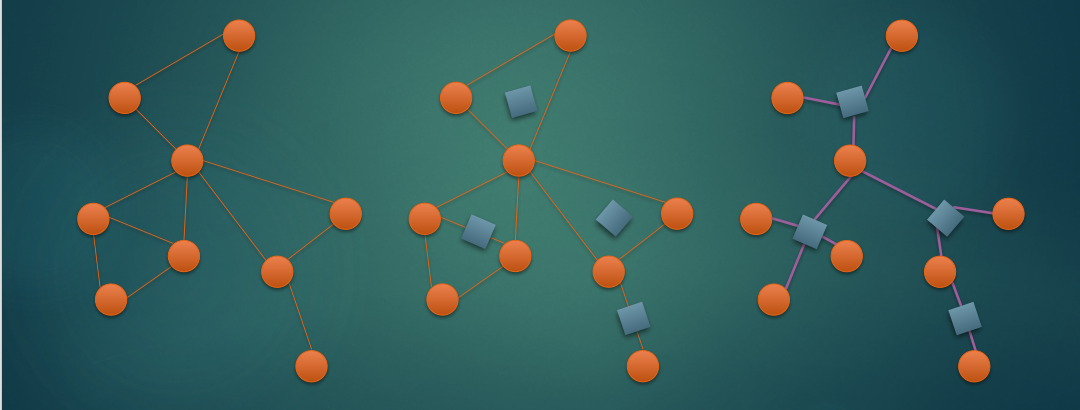
性质

1. 一定是个森林
2. 每个点双有唯一的方点
3. 圆点方点相间分布，相同点不相邻

等等

例子 1

题面

求可以出现在两点之间的简单路路径上的点的最大权值，不带修改

分析

考虑用圆方树来解决

设圆点权值为本身，方点权值为点双中的最大权值

那么就是树上的路径最大权值

例子 2

还是上面的题，可以修改一个点的权值

类似题UOJ

用老方法

每次修改时更改圆点连接的所有方点

没了？

不存在的，这样每次修改是\(O(n)\)的，容易被卡

换一种定义：方点权值不包括它的父亲圆点

那么每次修改就只要修改圆点的父亲

注意如果\(lca\)是方点，还要算上它父亲方点的权值

堆+线段树(zkw辣)+树剖+圆方树+tarjan

UOJ代码

# include <bits/stdc++.h>
# define RG register
# define IL inline
# define Fill(a, b) memset(a, b, sizeof(a))
using namespace std;
typedef long long ll;
const int _(4e5 + 5);

IL int Input(){
    RG int x = 0, z = 1; RG char c = getchar();
    for(; c < '0' || c > '9'; c = getchar()) z = c == '-' ? -1 : 1;
    for(; c >= '0' && c <= '9'; c = getchar()) x = (x << 1) + (x << 3) + (c ^ 48);
    return x * z;
}

struct Edge{
	int next[_], first[_], to[_], cnt;

	IL void Init(){
		Fill(first, -1);
	}

	IL void Add(RG int u, RG int v){
		next[cnt] = first[u], to[cnt] = v, first[u] = cnt++;
	}
} G1, G2;
struct Segment{
	int mn[_ << 2], M;

	IL void Init(RG int n){
		Fill(mn, 127);
		for(M = 1; M < n; M <<= 1);
	}

	IL void Update(RG int x, RG int y){
		x += M - 1, mn[x] = y;
		for(x >>= 1; x; x >>= 1) mn[x] = min(mn[x << 1], mn[x << 1 | 1]);
	}

	IL int Query(RG int l, RG int r){
		RG int ret = 2e9;
		for(l += M - 2, r += M; l ^ r ^ 1; l >>= 1, r >>= 1){
			if(~l & 1) ret = min(ret, mn[l ^ 1]);
			if(r & 1) ret = min(ret, mn[r ^ 1]);
		}
		return ret;
	}
} T;
struct Heap{
	priority_queue <int> Q1, Q2;

	IL void Push(RG int x){
		Q1.push(-x);
	}

	IL void Del(RG int x){
		Q2.push(-x);
	}

	IL int Top(){
		while(!Q2.empty() && Q1.top() == Q2.top()) Q1.pop(), Q2.pop();
		return -Q1.top();
	}
} Q[_];
int tmp, n, m, q, val[_], dfn[_], low[_], Index, S[_];
int size[_], top[_], fa[_], deep[_], son[_];

IL void Tarjan(RG int u){
	dfn[u] = low[u] = ++Index, S[++S[0]] = u;
	for(RG int e = G1.first[u]; e != -1; e = G1.next[e]){
		RG int v = G1.to[e], x;
		if(!dfn[v]){
			Tarjan(v), low[u] = min(low[u], low[v]);
			if(low[v] >= dfn[u]){
				val[++n] = 2e9, x = 0;
				do{
					x = S[S[0]--];
					G2.Add(n, x), G2.Add(x, n);
				} while(x != v);
				G2.Add(n, u), G2.Add(u, n);
			}
		}
		else low[u] = min(low[u], dfn[v]);
	}
}

IL void Dfs1(RG int u){
	size[u] = 1;
	if(u <= tmp && fa[u]) Q[fa[u]].Push(val[u]);
	for(RG int e = G2.first[u]; e != -1; e = G2.next[e]){
		RG int v = G2.to[e];
		if(size[v]) continue;
		fa[v] = u, deep[v] = deep[u] + 1;
		Dfs1(v);
		size[u] += size[v];
		if(size[v] > size[son[u]]) son[u] = v;
	}
}

IL void Dfs2(RG int u, RG int Top){
	dfn[u] = ++Index, top[u] = Top;
	if(son[u]) Dfs2(son[u], Top);
	for(RG int e = G2.first[u]; e != -1; e = G2.next[e])
		if(!dfn[G2.to[e]]) Dfs2(G2.to[e], G2.to[e]);
}

IL int Query(RG int u, RG int v){
	RG int ret = 2e9;
	while(top[u] ^ top[v]){
		if(deep[top[u]] > deep[top[v]]) swap(u, v);
		ret = min(ret, T.Query(dfn[top[v]], dfn[v]));
		v = fa[top[v]];
	}
	if(dfn[u] > dfn[v]) swap(u, v);
	ret = min(ret, T.Query(dfn[u], dfn[v]));
	if(u > tmp) ret = min(ret, val[fa[u]]);
	return ret;
}

int main(RG int argc, RG char* argv[]){
	G1.Init(), G2.Init();
	tmp = n = Input(), m = Input(), q = Input();
	for(RG int i = 1; i <= n; ++i) val[i] = Input();
	for(RG int i = 1; i <= m; ++i){
		RG int u = Input(), v = Input();
	    G1.Add(u, v), G1.Add(v, u);
	}
	for(RG int i = 1; i <= tmp; ++i) if(!dfn[i]) Tarjan(i);
	Fill(dfn, 0), Index = 0, T.Init(n);
	Dfs1(1), Dfs2(1, 1);
	for(RG int i = 1; i <= n; ++i) T.Update(dfn[i], val[i]);
	for(RG int i = tmp + 1; i <= n; ++i) T.Update(dfn[i], Q[i].Top());
	for(RG int i = 1, a, b; i <= q; ++i){
		RG char op; scanf(" %c", &op);
		a = Input(), b = Input();
		if(op == 'C'){
			if(fa[a]) Q[fa[a]].Del(val[a]);
			val[a] = b, T.Update(dfn[a], val[a]);
			if(fa[a]) Q[fa[a]].Push(val[a]);
			if(fa[a]) T.Update(dfn[fa[a]], Q[fa[a]].Top());
		}
		else printf("%d\n", Query(a, b));
	}
	return 0;
}