Huffman的应用之文件压缩与解压缩

文件压缩与解压缩>

     近期这段时间一直在学习树的这样的数据结构,也接触到了Huffman树以及了解了什仫是Huffman编码,而我们经常使用的zip压缩也是利用的Huffman编码的特性，那仫是不是能够自己实现一个文件压缩呢？当然能够了.在文件压缩中我实现了Huffman树和建堆Heap的代码，zip压缩的介绍>

http://www.cricode.com/3481.html

    以下開始介绍自己实现的文件压缩的思路和问题...

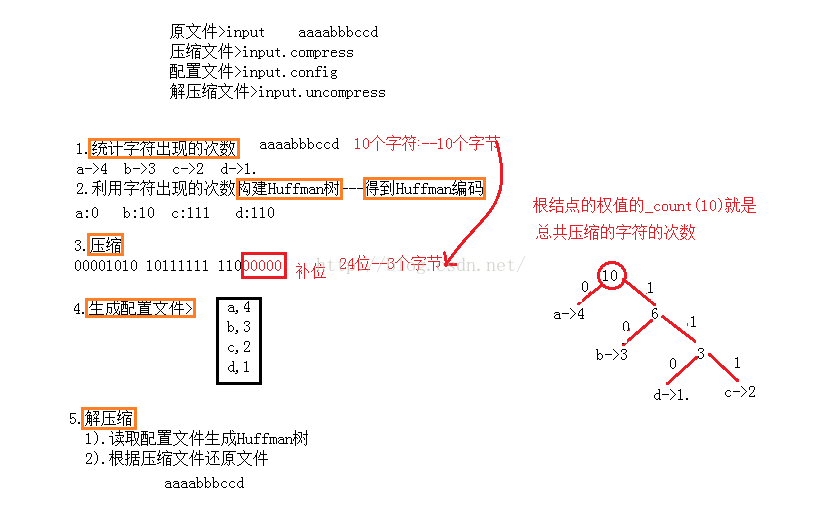
     1).统计>读取一个文件统计这个文件里字符出现的次数.

     2).建树>以字符出现的次数作为权值使用贪心算法构建Huffman树(依据Huffman树的特性>字符出现次数多的一定靠近根结点，出现次数少的一定远离根结点).

     3).生成Huffman编码>规则左0右1.

     4).压缩>再次读取文件,依据生成的Huffman编码压缩文件.

     5).生成配置文件>将字符以及字符出现的次数写进配置文件里.

     6).解压缩>利用配置文件还原出Huffman树,依据压缩文件还原出原文件.

     7).測试>推断解压是否正确须要推断原文件和解压缩之后的文件是否同样,利用Beyond Compare软件进行对照.

     以下是我举的一个简单的范例，模拟压缩和解压缩的过程，希望有读者有帮助

     

     利用Beyond Compare软件进行对照>

    

watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQv/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center" />

    

     在实现中出现了非常多的问题,以下我提出几个easy犯的问题,仅供參考

     1).在使用贪心算法构建Huffman树的时候,假设我们以unsigned char一个字节来存储它总共同拥有2^8=256个字符,假设将全部的字符都构建Huffman树,这不仅减少了效率还将分配极大的内存.所以我设立了非法值这个概念,仅仅有当字符出现的次数不为0的时候才将该字符构建到Huffman树中.

     2).在写压缩文件的时候我们是将字符相应的Huffman编码转化为相应的位,每当填满一个字节(8位)后再写入压缩文件里.假设最后一个字节没有填满我们就将已经填的位移位空出后几个位置,将未满的位置补0补满一个字节再写入压缩文件里.

     3).假设我们将源文件压缩之后再去解压,由于你的Huffman树和Huffman编码都是在压缩函数中得到的,此时再去解压那仫你的Huffman编码以及不存在了该怎样去还原文件呢？这就是为什仫要生成配置文件的原因了,在配置文件里写入了字符以及字符出现的次数.在解压缩中依据配置文件构建新的Huffman树.

    4).由压缩文件还原文件的时候怎样知道压了多少个字符呢？也就是说由于我们在压缩的时候最后一个字节是补了0的在解压缩的时候可能会把这个补的位当成字符的编码来处理.一种想法是在统计字符出现的次数的时候设置一个变量,每读取一个字符该变量就加1,最后将该变量写进配置文件里.第二种想法就是依据根结点的权值,通过上述简单的实例观察可知根结点权值中的_count就是字符出现的次数.

    攻克了以上几个问题,我的程序已经能够压缩那256个字符并正确的还原了,那仫假设是大文件或者是汉字，图片以及音频视频呢？

     1).由于有些特殊的字符编码，所以我们统计字符出现的次数的时候应该用的是unsigned char,刚開始我用的文件结束标志是EOF在ASII中它的编码是-1此时已经不能够用EOF来推断是否文件结束了，所以我用了feof这个函数来推断文件是否结束.

     2).统计字符出现次数应该用的类型是long long,这就攻克了大文件的压缩和解压缩的问题了.

     3).由于汉字。图片。视频这些在内存中是以二进制的形式存在的,所以我们将以文本形式打开读或者写的改动为以二进制的形式读或者写.

    为了验证大文件的压缩我找了一个8.09M的文件压缩之后是6.50M,而且能够正确还原.

    1).測试效率>

      

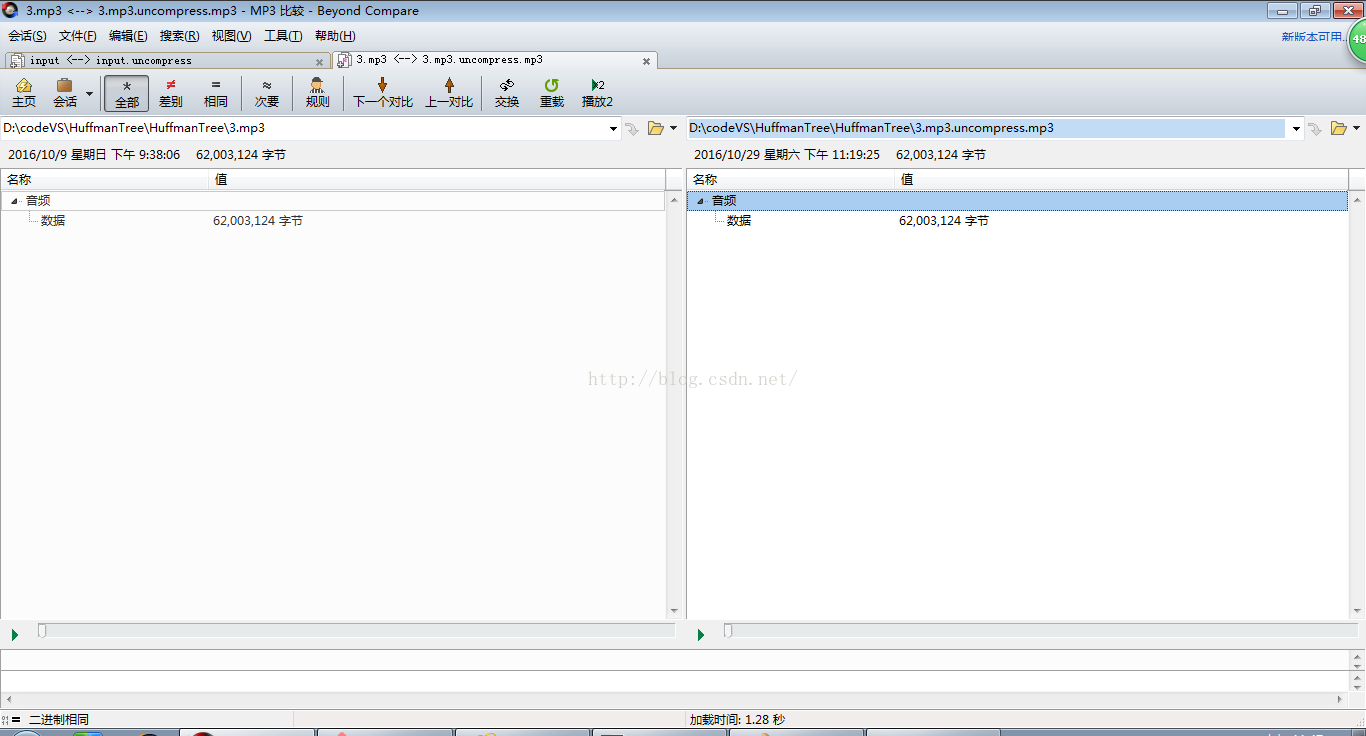
    2).利用Beyond Compare软件进行对照。假设一样说明压缩成功>

      

watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQv/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center" />

      

      

    

   

    

#define _CRT_SECURE_NO_WARNINGS 1
#pragma once

#include "Heap.h"

template<class T>
struct HuffmanTreeNode
{
	T _weight;
	HuffmanTreeNode<T> *_left;
	HuffmanTreeNode<T> *_right;
	HuffmanTreeNode<T> *_parent;
	HuffmanTreeNode(const T& w=T())
		:_weight(w)
		,_left(NULL)
		,_right(NULL)
		,_parent(NULL)
	{}
};

template<class T>
class HuffmanTree
{
	typedef HuffmanTreeNode<T> Node;
public:
	HuffmanTree()
		:_root(NULL)
	{}
	HuffmanTree(const T* a,size_t size)
		:_root(NULL)
	{
		_root=_CreatHuffmanTree(a,size);
	}
	//将未出现的字符过滤出来，不构造堆
	HuffmanTree(const T* a,size_t size,const T& invalid)
	{
		_root=_CreatHuffmanTree(a,size,invalid);
	}
	Node* GetRoot()
	{
		return _root;
	}
	~HuffmanTree()
	{
		_Destroy(_root);
	}
protected:
	Node *_CreatHuffmanTree(const T* a,size_t size)
	{
		struct NodeLess
		{
			bool operator()(Node *l,Node *r)const
			{
				return l->_weight < r->_weight;
			}
		};
		Heap<Node *,NodeLess> minHeap;
		//建立结点并放入vector中
		for (size_t i=0;i<size;++i)
		{
			Node *tmp=new Node(a[i]);
			minHeap.Push(tmp);
		}
		//取出较小的两个结点作为左右孩子并构建父结点
		while (minHeap.Size() > 1)
		{
			Node *left=minHeap.Top();
			minHeap.Pop();
			Node *right=minHeap.Top();
			minHeap.Pop();
			Node *parent=new Node(left->_weight + right->_weight);
			parent->_left=left;
			parent->_right=right;
			left->_parent=parent;
			right->_parent=parent;
			minHeap.Push(parent);
		}
		return minHeap.Top();
	}
	//思路相似不带过滤功能的
	Node *_CreatHuffmanTree(const T* a,size_t size,const T& invalid)
	{
		struct NodeLess
		{
			bool operator()(Node *l,Node *r)const
			{
				return l->_weight < r->_weight;
			}
		};
		Heap<Node *,NodeLess> minHeap;
		//建立结点并放入vector中
		for (size_t i=0;i<size;++i)
		{
			if(a[i] != invalid)
			{
				Node *tmp=new Node(a[i]);
				minHeap.Push(tmp);
			}
		}
		//取出较小的两个结点作为左右孩子并构建父结点
		while (minHeap.Size() > 1)
		{
			Node *left=minHeap.Top();
			minHeap.Pop();
			Node *right=minHeap.Top();
			minHeap.Pop();
			Node *parent=new Node(left->_weight + right->_weight);
			parent->_left=left;
			parent->_right=right;
			left->_parent=parent;
			right->_parent=parent;
			minHeap.Push(parent);
		}
		return minHeap.Top();
	}
	void _Destroy(Node *&root)
	{
		if(root == NULL)
			return ;
		Node *cur=root;
		if(cur)
		{
			_Destroy(cur->_left);
			_Destroy(cur->_right);
			delete cur;
			cur=NULL;
			return ;
		}
	}
protected:
	Node *_root;
};

void testHuffmanTree()
{
	int a[]={0,1,2,3,4,5,6,7,8,9};
	int size=sizeof(a)/sizeof(a[0]);
	HuffmanTree<int> ht(a,size);
}

 

#define _CRT_SECURE_NO_WARNINGS 1

#pragma once

//利用仿函数的特性实现代码的复用性
template<class T>
struct Small
{
	bool operator()(const T& l,const T& r)
	{
		return l < r;
	}
};

template<class T>
struct Large
{
	bool operator()(const T& l,const T& r)
	{
		return l > r;
	}
};

template<class T,class Compare=Large<T>>  //缺省是建小堆
class Heap
{
public:
	Heap()
	{}
	Heap(const T *a,int size)
	{
		assert(a);
		_a.reserve(size);
		for (int i=0;i<size;++i)
		{
			_a.push_back(a[i]);
		}
		//建堆的时候从倒数第一个非叶子结点開始.
		for (int j=(size-2)/2;j>=0;--j)
		{
			_AdjustDown(j);
		}
	}
	void Push(const T& x)
	{
		_a.push_back(x);
		_AdjustUp(_a.size()-1);
	}
	void Pop()
	{
		assert(!_a.empty());
		swap(_a[0],_a[_a.size()-1]);
		_a.pop_back();
		_AdjustDown(0);
	}
	size_t Size()
	{
		return _a.size();
	}
	bool Empty()
	{
		return _a.empty();
	}
	const T& Top()const
	{
		assert(!_a.empty());
		return _a[0];
	}
	void Display()
	{
		for (size_t i=0;i<_a.size();++i)
		{
			cout<<_a[i]<<" ";
		}
		cout<<endl;
	}
protected:
	void _AdjustDown(int root)
	{
		int parent=root;
		size_t child=2*root+1;
		while (child < _a.size())
		{
			Compare com;
			//child指向左右孩子中较大的那个数
			//if (child+1 < _a.size()
			//	&& _a[child+1] > _a[child])
			if(child+1 < _a.size()
				&& com(_a[child+1],_a[child]))
			{
				child++;
			}
			//if (_a[child] > _a[parent])
			if(com(_a[child],_a[parent]))
			{
				swap(_a[child],_a[parent]);
				parent=child;
				//初始的child默认指向左孩子
				child=2*parent+1;
			}
			else
				break;
		}
	}
	void _AdjustUp(int child)
	{
		while (child > 0)
		{
			int parent=(child-1)/2;
			Compare com;
			//if (_a[child] > _a[parent])
			if(com(_a[child],_a[parent]))
			{
				swap(_a[child],_a[parent]);
				child=parent;
			}
			else
				//插入的数据比父节点的数据域小
				break;
		}
	}
protected:
	vector<T> _a;
};
//利用堆解决优先级队列的问题
template<class T,class Compare=Large<T>>
class PriorityQueue
{
public:
	PriorityQueue(int *a,int size)
		:_pq(a,size)
	{}
	void Push(const T& x)
	{
		_pq.Push(x);
	}
	void Pop()
	{
		_pq.Pop();
	}
	const T& Top()const
	{
		return _pq.Top();
	}
	void Display()
	{
		_pq.Display();
	}
protected:
	Heap<T,Compare> _pq;
};

 

 

#define _CRT_SECURE_NO_WARNINGS 1

#pragma once

#include "HuffmanTree.h"

typedef long long Type;

struct CharInfo
{
	unsigned char _ch;     //出现的字符
	Type _count;           //统计次数
	string _code;          //Huffman编码
	CharInfo(Type count=0)
		:_ch(0)
		,_count(count)
		,_code("")
	{}
	//重载相应的操作符
	CharInfo operator + (const CharInfo& fc)const
	{
		return CharInfo(_count + fc._count);
	}
	bool operator != (const CharInfo fc)const
	{
		return _count != fc._count;
	}
	bool operator < (const CharInfo& fc)const
	{
		return _count < fc._count;
	}
};

class FileCompress
{
public:
	//默认的构造函数
	FileCompress()
	{
		for(size_t i=0;i<256;++i)
		{
			_infos[i]._ch=i;
		}
	}
	string Compress(const char *filename)
	{
		assert(filename);
		FILE *pf=fopen(filename,"rb");
		assert(pf);
		unsigned char ch=fgetc(pf);
		//统计字符出现的次数
		while (!feof(pf))
		{
			_infos[ch]._count++;
			ch=fgetc(pf);
		}
		//以该字符出现的次数构建一颗HuffmanTree.
		CharInfo invalid;   //非法值
		HuffmanTree<CharInfo> ht(_infos,256,invalid);
		//生成Huffman编码
		string code;
		_CreatHuffmanCode(ht.GetRoot(),code);
		//_CreatHuffmanCode(ht.GetRoot());
		//压缩文件
		fseek(pf,0,SEEK_SET);          //回到文件头
		string compressfile=filename;
		compressfile += ".compress";   //压缩后的文件名称
		FILE *fin=fopen(compressfile.c_str(),"wb");
		assert(fin);
		size_t pos=0;                  //记录位数
		unsigned char value=0;
		ch=fgetc(pf);
		while (!feof(pf))
		{
			string &code=_infos[ch]._code;
			for (size_t i=0;i<code.size();++i)
			{
				value <<= 1;
				if(code[i] == '1')
					value |= 1;
				else
					value |= 0;    //do-nothing
				++pos;
				if(pos == 8)     //满一个字节
				{
					fputc(value,fin);
					value=0;
					pos=0;
				}
			}
			ch=fgetc(pf);
		}
		if(pos)      //解决不足8位的情况.
		{
			value <<= (8-pos);
			fputc(value,fin);
		}
		//配置文件--便于重建Huffman树
		string configfilename=filename;
		configfilename += ".config";
		FILE *finconfig=fopen(configfilename.c_str(),"wb");
		assert(finconfig);
		string line;
		char buff[128];
		for (size_t i=0;i<256;++i)
		{
			//一行一行的读
			if (_infos[i]._count)
			{
				line += _infos[i]._ch;
				line += ",";
				line += _itoa(_infos[i]._count,buff,10);
				line += "\n";
				//fputs(line.c_str(),finconfig);
				fwrite(line.c_str(),1,line.size(),finconfig);
				line.clear();
			}
		}
		fclose(pf);
		fclose(fin);
		fclose(finconfig);
		return compressfile;
	}
	string UnCompress(const char *filename)
	{
		assert(filename);
		string configfilename=filename;
		size_t index=configfilename.rfind(".");
		configfilename=configfilename.substr(0,index);
		configfilename += ".config";
		FILE *foutconfig=fopen(configfilename.c_str(),"rb");
		assert(foutconfig);
		string line;
		//读取配置文件--获取字符出现的次数
		unsigned char ch=0;
		while (ReadLine(foutconfig,line))
		{
			if(line.empty())
			{
				line += '\n';
				continue;
			}
			//读到空行
			ch=line[0];
			_infos[ch]._count = atoi(line.substr(2).c_str());
			line.clear();
		}
		//构建Huffman树
		CharInfo invalid;
		HuffmanTree<CharInfo> hft(_infos,256,invalid);
		//根结点的权值也就是字符出现的次数总和
		HuffmanTreeNode<CharInfo> *root=hft.GetRoot();
		Type charcount=root->_weight._count;
		//解压缩
		string uncompressfilename=filename;
		index=uncompressfilename.rfind(".");
		uncompressfilename=uncompressfilename.substr(0,index);
		uncompressfilename += ".uncompress";
		FILE *fin=fopen(uncompressfilename.c_str(),"wb");
		assert(fin);
		//由压缩文件还原文件
		string compressfilename=filename;
		FILE *fout=fopen(compressfilename.c_str(),"rb");
		assert(fout);

		HuffmanTreeNode<CharInfo> *cur=root;
		int pos=7;
		ch=fgetc(fout);
		while (charcount > 0)
		{
			while (cur)
			{
				if(cur->_left == NULL && cur->_right == NULL)
				{
					//叶子结点
					fputc(cur->_weight._ch,fin);
					cur=root;
					--charcount;
					if (charcount == 0)   //全部的字符都处理完毕
						break;
				}
				if (ch & (1 << pos))    //检查字符的每一个位
					cur=cur->_right;    //1向右走
				else
					cur=cur->_left;     //0向左走
				--pos;
				if(pos < 0)             //一个字节解压完毕
				{
					ch=fgetc(fout);
					pos=7;
				}
			}
		}
		fclose(foutconfig);
		fclose(fin);
		fclose(fout);
		return uncompressfilename;
	}
	//读取一行字符并放在line中
	bool ReadLine(FILE *fout,string& line)
	{
		int ch=fgetc(fout);
		if(ch == EOF)
			return false;
		while (ch != EOF && ch != '\n')
		{
			line += ch;
			ch=fgetc(fout);
		}
		return true;
	}
protected:
	//递归的方法求HuffmanTreeCode
	void _CreatHuffmanCode(HuffmanTreeNode<CharInfo> *root,string &code)
	{
		if(root == NULL)
			return ;
		_CreatHuffmanCode(root->_left,code+'0');
		_CreatHuffmanCode(root->_right,code+'1');
		if(root->_left == NULL && root->_right == NULL)   //叶子结点
		{
			_infos[root->_weight._ch]._code=code;
		}
	}
	//非递归求HuffmanTreeCode
	void _CreatHuffmanCode(HuffmanTreeNode<CharInfo> *root)
	{
		if(root == NULL)
			return ;
		_CreatHuffmanCode(root->_left);
		_CreatHuffmanCode(root->_right);
		if(root->_left == NULL && root->_right == NULL)   //叶子结点
		{
			string& code=_infos[root->_weight._ch]._code;
			HuffmanTreeNode<CharInfo> *cur=root;
			HuffmanTreeNode<CharInfo> *parent=root->_parent;
			while (parent)
			{
				if(parent->_left == cur)
					code.push_back('0');    //左0
				else
					code.push_back('1');    //右1
				cur=parent;
				parent=cur->_parent;
			}
			//编码是从根到叶子结点的，须要逆置
			reverse(code.begin(),code.end());
		}
	}
protected:
	CharInfo _infos[256];
};

void testFileCompress()
{
	FileCompress fc;
	cout<<"開始压缩"<<endl;
	cout<<"压缩用时:";
	int start=GetTickCount();
	fc.Compress("2.png");    //input input.BIG 3.mp3
	int end=GetTickCount();
	cout<<end-start<<endl;
	cout<<"開始解压"<<endl;
	cout<<"解缩用时:";
	start=GetTickCount();
	fc.UnCompress("2.png.compress"); //input.compress input.BIG.compress 3.mp3
	end=GetTickCount();
	cout<<end-start<<endl;
}

void testFileUncompress()
{
	FileCompress fc;
	cout<<"開始解压"<<endl;
	cout<<"解缩用时:";
	int start=GetTickCount();
	fc.UnCompress("2.png");
	int end=GetTickCount();
	cout<<end-start<<endl;
}

 

    

     经过測试这个小项目已经能够压缩并还原一些文件了，眼下还没有发现什仫大的Bug,假设有童鞋发现请第一时间告诉我哦...