codeforces 691E 矩阵快速幂+dp

传送门：https://codeforces.com/contest/691/problem/E

题意：给定长度为n的序列，从序列中选择k个数（可以重复选择），使得得到的排列满足xi与xi+1异或的二进制中1的个数是3的倍数。问长度为k的满足条件的序列有多少种？

题解：dp状态定义为，在前i个数中以a_j为结尾的方案数量

则转移为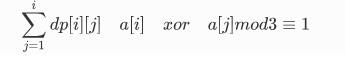

因为是求和的转移，可以用矩阵快速幂将O（n）的求和加速为log级别

接下来的问题就是然后填系数了，因为要累加，所以只要时，我们将矩阵的第i行第j列的系数填为1即可

目的：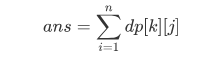

由于也是一个求和的转移，所以实际上我们将所得到的系数矩阵求一个k次幂即可得到答案

总复杂度为矩阵乘法的复杂度*矩阵快速幂的复杂度 O(n^3*log₂n)

代码：

/**
 *　　　　　　　　┏┓　　 　┏┓
 * 　　　　　　　┏┛┗━━━━━━━┛┗━━━┓
 * 　　　　　　　┃　　　　　　　┃ 　
 * 　　　　　　　┃　　　━　　 　┃
 * 　　　　　　　┃　＞　　　＜　┃
 * 　　　　　　　┃　　　　　　　┃
 * 　　　　　　　┃...　⌒　... 　┃
 * 　　　　　　　┃　　　　　　　┃
 * 　　　　　　　┗━┓　　　┏━┛
 * 　　　　　　　　　┃　　　┃　Code is far away from bug with the animal protecting　　　　　　　　　　
 * 　　　　　　　　　┃　　　┃   神兽保佑,代码无bug
 * 　　　　　　　　　┃　　　┃　　　　　　　　　　　
 * 　　　　　　　　　┃　　　┃  　　　　　　
 * 　　　　　　　　　┃　　　┃
 * 　　　　　　　　　┃　　　┃　　　　　　　　　　　
 * 　　　　　　　　　┃　　　┗━━━┓
 * 　　　　　　　　　┃　　　　　　　┣┓
 * 　　　　　　　　　┃　　　　　　　┏┛
 * 　　　　　　　　　┗┓┓┏━┳┓┏┛
 * 　　　　　　　　　　┃┫┫　┃┫┫
 * 　　　　　　　　　　┗┻┛　┗┻┛
 */
// warm heart, wagging tail,and a smile just for you!
//                                                                     ███████████
//                                                                   ███╬╬╬╬╬╬╬╬╬╬███
//                                                                ███╬╬╬╬╬████╬╬╬╬╬╬███
//                                            ███████████       ██╬╬╬╬╬████╬╬████╬╬╬╬╬██
//                                      █████████╬╬╬╬╬████████████╬╬╬╬╬██╬╬╬╬╬╬███╬╬╬╬╬██
//                               ████████╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬█████████╬╬╬╬╬╬██╬╬╬╬╬╬╬██
//                             ████╬██╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬█████████╬╬╬╬╬╬╬╬╬╬╬██
//                           ███╬╬╬█╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬██╬╬███╬╬╬╬╬╬╬█████
//                         ███╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬██╬╬╬████████╬╬╬╬╬██
//                       ███╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬███╬╬╬╬╬╬╬╬╬███
//                     ███╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬█████╬╬╬╬╬╬╬██
//                 ████╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬████╬╬╬╬╬████
//     █████████████╬╬╬╬╬╬╬╬██╬╬╬╬╬████╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬█████╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬███╬╬╬╬██████
//   ████╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬██╬╬██████╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬██████╬╬╬╬╬╬╬███████████╬╬╬╬╬╬╬╬██╬╬╬██╬╬╬██
// ███╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬██╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬██╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬████╬╬╬╬╬╬╬╬╬╬╬█╬╬╬╬╬╬╬██╬╬╬╬╬╬╬╬██
// ██╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬██╬╬╬╬▓▓▓▓▓▓╬╬╬████╬╬████╬╬╬╬╬╬╬▓▓▓▓▓▓▓▓██╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬██╬╬╬╬╬╬╬███
// ██╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬██████▓▓▓▓▓▓▓╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬▓▓▓▓▓▓▓██╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬██╬╬╬╬█████
// ███╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬███╬╬╬╬╬██╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬█████╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬████████
//   ███╬╬╬╬╬╬╬╬╬╬╬╬╬█████╬╬╬╬╬╬╬╬██╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬███╬╬██╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬██
//       ██████████████  ████╬╬╬╬╬╬███████████████████████████╬╬╬╬╬██╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬╬████
//                         ███████                           █████  ███████████████████
#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> pil;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define bug printf("*********\n")
#define FIN freopen("input.txt","r",stdin);
#define FON freopen("output.txt","w+",stdout);
#define IO ios::sync_with_stdio(false),cin.tie(0)
#define debug1(x) cout<<"["<<#x<<" "<<(x)<<"]\n"
#define debug2(x,y) cout<<"["<<#x<<" "<<(x)<<" "<<#y<<" "<<(y)<<"]\n"
#define debug3(x,y,z) cout<<"["<<#x<<" "<<(x)<<" "<<#y<<" "<<(y)<<" "<<#z<<" "<<z<<"]\n"
LL read() {
    int x = , f = ; char ch = getchar();
    while(ch < '' || ch > '') {
        if(ch == '-')f = -;
        ch = getchar();
    }
    while(ch >= '' && ch <= '') {
        x = x *  + ch - '';
        ch = getchar();
    }
    return x * f;
}
const double eps = 1e-;
const int mod = 1e9 + ;
const int maxn = 3e5 + ;
const int INF = 0x3f3f3f3f;
const LL INFLL = 0x3f3f3f3f3f3f3f3f;
// 给定长度为n的序列，从序列中选择k个数（可以重复选择），
// 使得得到的排列满足xi与xi+1异或的二进制中1的个数是3的倍数。
// 问长度为k的满足条件的序列有多少种？
LL a[maxn];
LL dp[][];
struct matrix {//矩阵
    int n;//长
    int m;//宽
    long long a[][];
    matrix() {//构造函数
        n = ;
        m = ;
        memset(a, , sizeof(a));
    }
    matrix(int x, int y) {
        n = x;
        m = y;
        memset(a, , sizeof(a));
    }
    void print() {
        for(int i = ; i <= n; i++) {
            for(int j = ; j <= m; j++) {
                printf("%d ", a[i][j]);
            }
            printf("\n");
        }
    }
    void setv(int x) {//初始化
        if(x == ) {
            memset(a, , sizeof(a));
        }
        if(x == ) {
            memset(a, , sizeof(a));
            for(int i = ; i <= n; i++) a[i][i] = ;
        }
    }
    friend matrix operator *(matrix x, matrix y) { //矩阵乘法
        matrix tmp = matrix(x.n, y.m);
        for(int i = ; i <= x.n; i++) {
            for(int j = ; j <= y.m; j++) {
                tmp.a[i][j] = ;
                for(int k = ; k <= y.n; k++) {
                    tmp.a[i][j] += (x.a[i][k] * y.a[k][j]) % mod;
                }
                tmp.a[i][j] %= mod;
            }
        }
        return tmp;
    }
};
int n;
LL  k;
matrix fast_pow(matrix x, long long k) { //矩阵快速幂
    matrix ans = matrix(n, n);
    ans.setv();//初始化为1
    while(k > ) { //类似整数快速幂
        if(k & ) {
            ans = ans * x;
        }
        k >>= ;
        x = x * x;
    }
    return ans;
}

int cal(LL x) {
    int cnt = ;
    while(x) {
        if(x &  ) {
            cnt++;
        }
        x /= ;
    }
    return cnt;
}
int main() {
#ifndef ONLINE_JUDGE
    FIN
#endif
    scanf("%d%lld", &n, &k);
    for(int i = ; i <= n; i++) {
        scanf("%lld", &a[i]);
    }
    matrix xor_mat = matrix(n, n);
    for(int i = ; i <= n; i++) {
        for(int j = ; j <= n; j++) {
            if(cal(a[i]^a[j]) %  ==  )    xor_mat.a[i][j] = ;
            else xor_mat.a[i][j] = ;
        }
    }
    xor_mat = fast_pow(xor_mat, k - );
    LL ans = ;
    for(int i = ; i <= n; i++) {
        for(int j = ; j <= n; j++) {
            ans += xor_mat.a[i][j];
        }
        ans %= mod;
    }
    cout << ans << endl;
    return ;
}