贝塞尔曲线 WPF MVVM N阶实现 公式详解+源代码下载

源代码下载

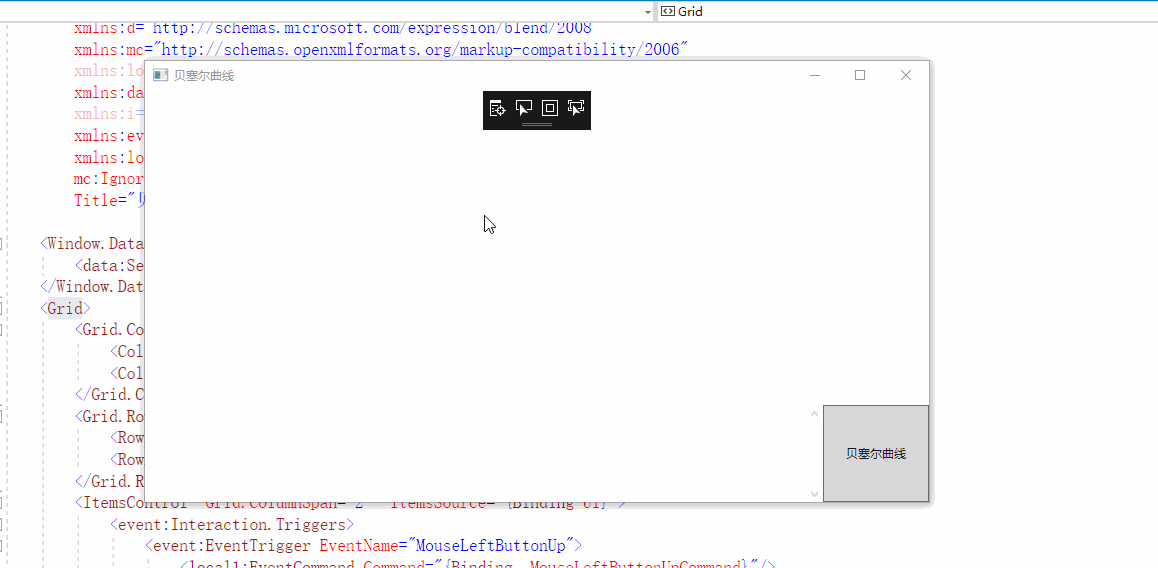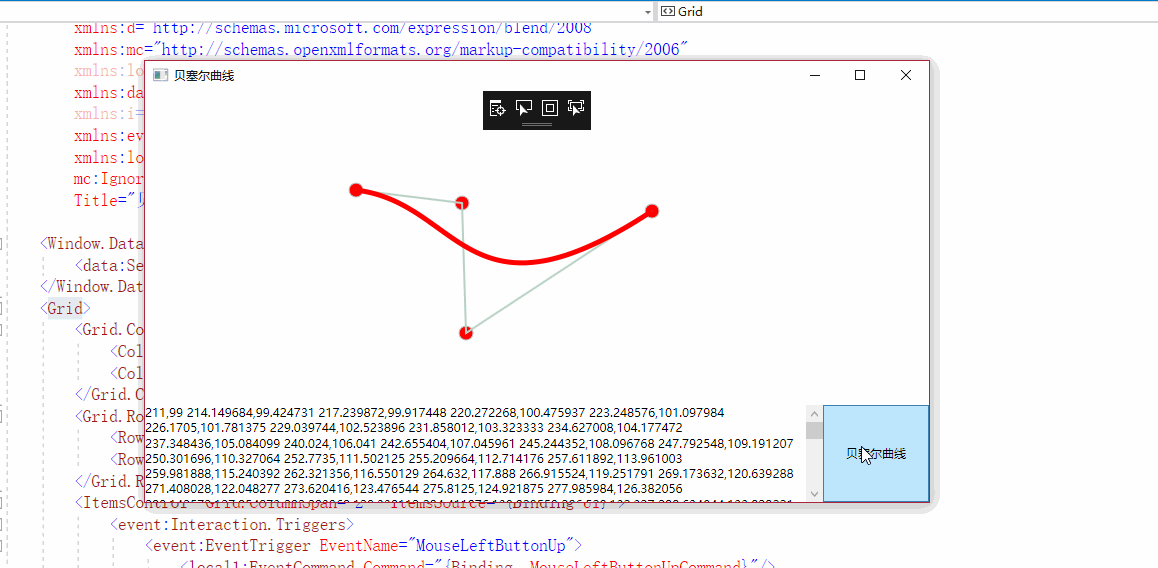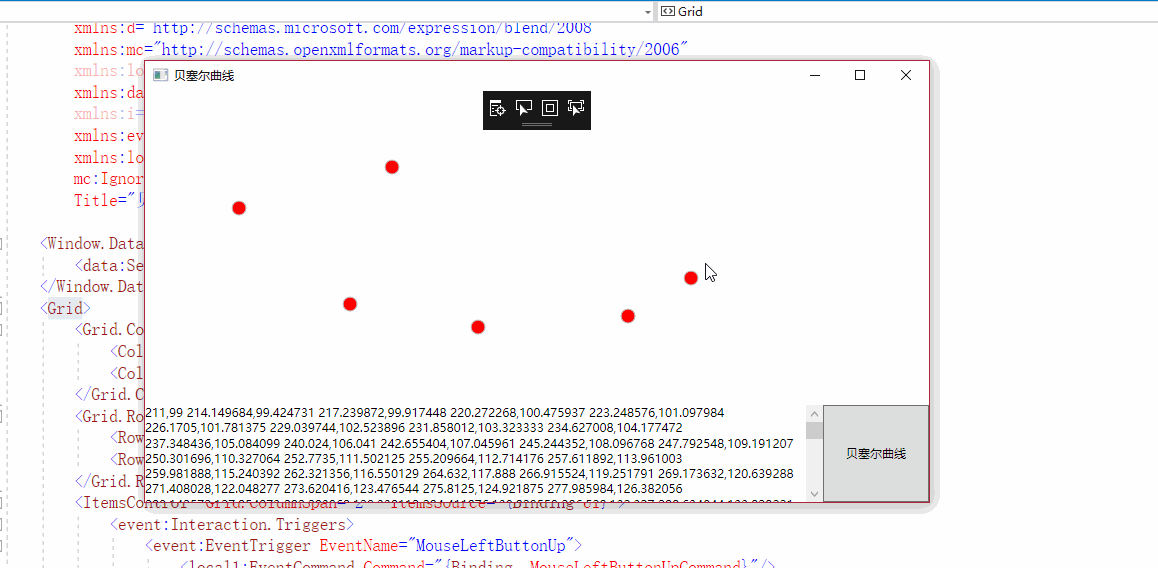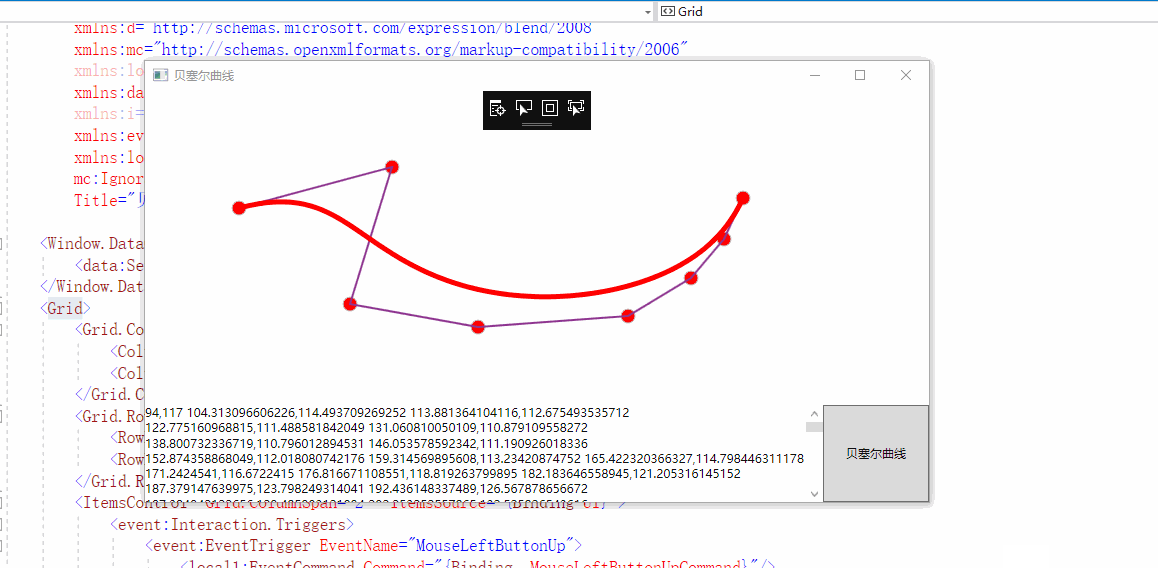
效果图：

本程序主要实现：

• N阶贝塞尔曲线（通用公式）

本程序主要使用技术

• MVVM
• InterAction 事件绑定
• 动态添加Canvas的Item

第一部分公式：

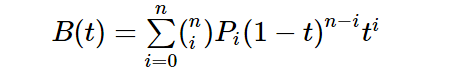
• n=有效坐标点数量
• i=坐标点的下标
• P是坐标
• t是时间0~1之间

有效坐标点是坐标点的数量减1

计算坐标时分开计算，x，y时分别计算两边

至于括号内上n下i是组合数

计算方法是：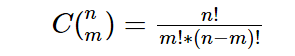

换成贝塞尔的公式中的组合数是：

剩下部分应该是很简单了。

因为是求和，所以先是代入公式最后相加即可

例子（摘自百度）

3阶

2阶

现在给出代码的部分

阶乘代码：

 private int Factorial(int n)
        {
            if (n == )
            {
                return ;
            }
            else
            {
                return n * Factorial(n - );
            }

        }

组合数公式代码：

        private int GetCA(int r, int n) => Factorial(r) / (Factorial(n) * Factorial((r - n)));

贝塞尔

  /// <summary>
        /// 求单坐标贝塞尔公式
        /// </summary>
        /// <param name="Max">最大有效坐标点的数量</param>
        /// <param name="Index">需要计算的坐标点的下标</param>
        /// <param name="Time">时间0~1</param>
        /// <param name="P">单个坐标值（x或者y）</param>
        /// <returns></returns>
        private double GetPoints(int Max, int Index, double Time, double P)
        {
            var C = GetCA(Max, Index);
            var T1 = Math.Pow(Time, Index);
            var T2 = Math.Pow(( - Time), Max - Index);
            return (C * T1 * T2 * P);
        }

使用方式

  private void SetPoints(Polyline polyline)
        {
            polyline.Points.Clear();
            double ax = ;
            double ay = ;
            for (double t = 0.00; t < 1.01; t += 0.01)
            {
                for (int i = ; i < Points.Count; i++)
                {
                    ax += GetPoints(Points.Count - , i, t, Points[i].X);
                    ay += GetPoints(Points.Count - , i, t, Points[i].Y);
                }
                //此处的ax ay为t时，i下标的有效Points[i].X 坐标点 和Points[i].Y坐标点的Points.Count - 1阶贝塞尔曲线
                polyline.Points.Add(new Point(ax, ay));
                ax = ;
                ay = ;
            }
            SetText(polyline.Points);
        }

第二部分 MVVM的事件绑定

MVVM事件绑定需要使用

 System.Windwos.Interactiivity.dll

一般来说使用NuGet搜索Expression.Blend.Sdk.WPF就可以了

使用方式为

先创建实现 TriggerAction<DependencyObject>接口类

 public class EventCommand : TriggerAction<DependencyObject>
    {
        public static readonly DependencyProperty CommandProperty =
       DependencyProperty.Register("Command", typeof(ICommand), typeof(EventCommand),
      null);

        public static readonly DependencyProperty CommandParameterProperty =
         DependencyProperty.Register("CommandParameter", typeof(object), typeof(EventCommand),
        null);

        public ICommand Command
        {
            get { return (ICommand)GetValue(CommandProperty); }
            set { SetValue(CommandProperty, value); }
        }

        public object CommandParameter
        {
            get { return GetValue(CommandParameterProperty); }
            set { SetValue(CommandParameterProperty, value); }
        }

        protected override void Invoke(object parameter)
        {
            if (this.AssociatedObject != null)
            {
                ICommand command = this.Command;
                if (command != null)
                {
                    if (this.CommandParameter != null)
                    {
                        if (command.CanExecute(this.CommandParameter))
                        {
                            command.Execute(this.CommandParameter);
                        }
                    }
                    else
                    {
                        if (command.CanExecute(parameter))
                        {
                            command.Execute(new Tuple<object, object>(this.AssociatedObject, parameter));
                        }
                    }
                }
            }
        }

    }

其次是在XAML页面添加引用

分别为

  <!--此处时引用interactivity的dll-->
 xmlns:event="http://schemas.microsoft.com/expression/2010/interactivity"
  <!--此处时引用刚才实现的接口类-->
xmlns:Action="clr-namespace:MVVM_贝塞尔曲线任意点实现.Command"

使用方式：

 <ItemsControl  Grid.ColumnSpan="2"  ItemsSource="{Binding UI}">
            <event:Interaction.Triggers>
                <!--此处EventName为事件标准名称-->
                <event:EventTrigger EventName="MouseLeftButtonUp">
                    <Action:EventCommand Command="{Binding  MouseLeftButtonUpCommand}"/>
                </event:EventTrigger>
            </event:Interaction.Triggers>
            <ItemsControl.ItemsPanel>
                <ItemsPanelTemplate>
                    <Canvas  Background="Transparent"/>
                </ItemsPanelTemplate>
            </ItemsControl.ItemsPanel>
            <ItemsControl.ItemContainerStyle>
                <Style>
                    <Setter Property="Canvas.Left" Value="{Binding X}"/>
                    <Setter Property="Canvas.Top"  Value="{Binding Y}"/>
                </Style>
            </ItemsControl.ItemContainerStyle>
            <ItemsControl.ItemTemplate>
                <DataTemplate>
                    <ContentControl Content="{Binding UI}"/>
                </DataTemplate>
            </ItemsControl.ItemTemplate>
        </ItemsControl>

VIewMolde部分则是正常使用即可

剩余部分

可以看看源代码