c++动态规划dp算法题

问题1：找硬币，换钱的方法

输入：

• penny数组代表所有货币的面值，正数不重复
• aim小于等于1000，代表要找的钱

输出：
换钱的方法总数

解法1：经典dp，空间复杂度O（n*aim）

class Exchange {
public:
    int countWays(vector<int> penny, int n, int aim) {
        if (penny.empty()||n == 0)
            return 0;
        vector<vector<int> > dp(n,vector<int>(aim+1)); //二维数组dp
        for (int i = 0;i < n;i++) {
            dp[i][0] = 1;
        }
        for (int j = 1;j < aim+1;j++) {
            dp[0][j] = j%penny[0] == 0?1:0;  //只需要算dp[0][j]
        }   

        for (int i = 1;i < n;i++) {
            for (int j = 1;j < aim+1;j++) {
                dp[i][j] = (j-penny[i]) >= 0?(dp[i-1][j] + dp[i][j-penny[i]]):dp[i-1][j];   //这是关键，不用管penny【i】到底使用了几次，直接减去1次使用就好
            }
        }
        return dp[n-1][aim];
    }
};

　　解法2：与上面的问题一样，只不过在求dp时只使用1维数组来做；使用迭代，时间复杂度一样：

class Exchange {
public:
    int countWays(vector<int> penny, int n, int aim) {
        vector<int> dp(aim + 1);
        for (int i = 0; i <= aim; i++)
            if (i % penny[0] == 0)
                dp[i] = 1;

        for (int i = 1; i < n; i++)
            for (int j = 1; j <= aim; j++)
                if ( j >= penny[i]) //条件，如果不满足就直接等于上轮的结果，不用做修改
                    dp[j] += dp[j - penny[i]];
        return dp[aim];
    }
};

问题2：跳台阶问题：

其实是斐波那契问题，f(n)=f(n-1)+f(n-2)

#include <iostream>
using namespace std;
int main(){
	int step;
	while(cin>>step){
		vector<int> dp(2,1); //初始化赋值
		dp[1]=2;
		int temp;
		for(int i=3;i<=step;i++){
			temp=dp[0];
            dp[0]=dp[1];
            dp[1]=dp[1]+temp;
		}
		if(step==1) dp[1]=1;;
		cout<<dp[1]<<endl;
	}
	return 0;
}

问题3：走矩阵，求路劲最小和，或者是求整个路径

• n×m的map，则 f(n,m)=min(f(n-1,m),f(n,m-1))+map[n][m]；
• 由于这里和问题1类似，可以只用到一个一维数组求解；

class MinimumPath {
public:
    int getMin(vector<vector<int> > map, int n, int m) {
        vector<int> dp(m,0);
        dp[0] = map[0][0];
        for (int i = 1,j = 0;i < m;i++,j++) {
            dp[i] = map[0][i]+dp[j];
        }

        for (int i = 1;i < n;i++) {
            dp[0] += map[i][0];     //不能忘了dp[0]的更新
            for (int j = 1;j < m;j++) {
                dp[j] = min(dp[j],dp[j-1])+map[i][j]; //如果求路径，则在这里记录，需要额外存储空间
            }
        }
        return dp[m-1];
    }
};

问题4：最长上升子序列问题（LIS）

解法：O（N方）用dp数组的dp[i]记录下以A[i]结尾的递增子序列中最长的长度，计算dp[i+1]时，遍历A[0~i]找到比A[i+1]小的元素，再比较与这些元素对应的dp数组中的值，找到最大的一个再加1，赋值给dp[i+1]。

class LongestIncreasingSubsequence {
public:
    int getLIS(vector<int> A, int n) {
        if (A.empty()||n == 0)
            return 0;
        vector<int> dp(n,0);
        dp[0] = 1;
        int resMax = 0;
        for (int i = 1;i < n;i++) {
            int tempMax = 0;
            for (int j = 0;j < i;j++) {
                if (A[i] > A[j])
                    tempMax = max(tempMax,dp[j]);
            }
            dp[i] = ++tempMax;
            resMax = max(resMax,dp[i]);  //记录最大的上升子序列长度，因为当前i可能并不在最长上升子序列中
        }
        return resMax;
    }
};

• 如上的实现复杂度为N方，可以增加归纳的假设，增加b[k]存储长度为k最长子序列最小结尾元素，那么可以利用二分查找，使用logn查找到插入点，对于每次比较，要么直接比较b【k】比它大直接k+1，更新b【k+1】，要么二分查找到位置，更新b【j】，所以最终复杂度为nlogn（如果数据量大的话，使用该算法较好）
• 参考 https://blog.csdn.net/netown_ethereal/article/details/24010381

问题5：最长公共子序列长度（LCS）

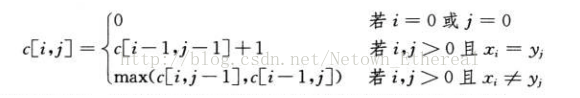
上图可以看出使用了斜侧的比较，所以不能再使用1维数组了

class LCS {
public:
    int findLCS(string A, int n, string B, int m) {
         if (A.empty()||n==0||B.empty()||m==0)
            return 0;
        vector<vector<int> > dp(n,vector<int>(m));
         //下面是两个for的初始化，当出现第一个相等的时，后面的都直接赋值为1；
        for (int i = 0;i < m;i++) {
            if (A[0] == B[i]) {
                for (int j = i;j < m;j++)
                    dp[0][j] = 1;
                break ;
            }
        }
        for (int i = 0;i < n;i++) {
            if (B[0] == A[i]) {
                for (int j = i;j < n;j++)
                    dp[j][0] = 1;
                break ;
            }
        }
        for (int i = 1;i < n;i++) {
            for (int j = 1;j < m;j++) {
                if (A[i] == B[j])
                    dp[i][j] = dp[i-1][j-1]+1;
                else
                    dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
            }
        }
        return dp[n-1][m-1];
    }
};

上面的方法中初始化第一行和第一列有点麻烦，增加了额外的语句，可以增加数组一行和一列来优化代码：

class LCS {
public:
    int findLCS(string A, int n, string B, int m) {
        vector<vector<int> > dp(n+1,vector<int>(m+1,0));
        for (int i =1;i<=n ;++i){
            for (int j=1; j<=m; ++j){
                if (A[i-1] == B[j-1]){
                    dp[i][j]  = dp[i-1][j-1]+1; //第1行也可以照此直接初始化
                }
                else {
                    dp[i][j] = max( dp[i-1][j] ,dp[i][j-1]);
                }
            }
        }
        return dp[n][m];
    }
};

问题6：背包

• N件物品，价值记录在数组V，重量记录在数组W，背包总重量最大为cap，要求总价值最大；

class Backpack {
public:
    int maxValue(vector<int> w, vector<int> v, int n, int cap) {
        if (w.empty()||v.empty()||n==0||cap==0)
            return 0;
        vector<vector<int> > dp(n,vector<int>(cap+1));

        for (int j = 1;j < cap+1;j++) {
            dp[0][j] = w[0] <= j?v[0]:0;
        }
        for (int i = 0;i < n;i++) {
            dp[i][0] = 0;
        }

        for (int i = 1;i < n;i++) {
            for (int j = 1;j < cap+1;j++) {
                if (w[i] > j)
                    dp[i][j] = dp[i-1][j];
                else
                    dp[i][j] = max(dp[i-1][j],v[i]+dp[i-1][j-w[i]]); //由于该问题每个物品最多只能放1件，如果不限制个数的话，则在这里修改条件
            }
        }
        return dp[n-1][cap];
    }
};

　　由于没有用到斜侧的比较，所以可以使用1维的数组：

class Backpack {
public:
    int maxValue(vector<int> w, vector<int> v, int n, int cap) {
        if (w.empty()||v.empty()||n==0||cap==0)
            return 0;
        vector<int> dp(cap+1,0);
        for (int i = 0;i < n;i++) {
             vector<int> last(dp);
            for (int j = 1;j < cap+1;j++) {
                dp[j] = j < w[i]?last[j]:max(last[j],v[i]+last[j-w[i]]);
            }
        }
        return dp[cap];
    }
};