Image Processing and Analysis_8_Edge Detection:Statistical edge detection_ learning and evaluating edge cues——2003
此主要讨论图像处理与分析。虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来,但鉴于它们与计算机视觉的紧密联系,以 及它们的出处,没有把它们纳入到图像处理与分析中来。同样,这里面也有一些 也可以划归到计算机视觉中去。这都不重要,只要知道有这么个方法,能为自己 所用,或者从中得到灵感,这就够了。
8. Edge Detection
边缘检测也是图像处理中的一个基本任务。传统的边缘检测方法有基于梯度
算子,尤其是 Sobel 算子,以及经典的 Canny 边缘检测。到现在,Canny 边缘检 测及其思想仍在广泛使用。关于 Canny
算法的具体细节可以在 Sonka 的书以及 canny 自己的论文中找到,网上也可以搜到。最快最直接的方法就是看 OpenCV
的源代码,非常好懂。在边缘检测方面,Berkeley 的大牛 J Malik 和他的学生 在 2004 年的 PAMI
提出的方法效果非常好,当然也比较复杂。在复杂度要求不高 的情况下,还是值得一试的。MIT的Bill Freeman早期的代表作Steerable
Filter 在边缘检测方面效果也非常好,并且便于实现。这里给出了几篇比较好的文献,
包括一篇最新的综述。边缘检测是图像处理和计算机视觉中任何方向都无法逃避 的一个问题,这方面研究多深都不为过。
[1980] theory of edge detection
[1983 Canny Thesis] find edge
[1986 PAMI] A Computational Approach to Edge Detection
[1990 PAMI] Scale-space and edge detection using anisotropic diffusion
[1991 PAMI] The design and use of steerable filters
[1995 PR] Multiresolution edge detection techniques
[1996 TIP] Optimal edge detection in two-dimensional images
[1998 PAMI] Local Scale Control for Edge Detection and Blur Estimation
[2003 PAMI] Statistical edge detection_ learning and evaluating edge cues
[2004 IEEE] Edge Detection Revisited
[2004 PAMI] Design of steerable filters for feature detection using canny-like criteria
[2004 PAMI] Learning to Detect Natural Image Boundaries Using Local Brightness, Color, and Texture Cues
[2011 IVC] Edge and line oriented contour detection State of the art
翻译
统计边缘检测_学习和评估边缘提示——http://tongtianta.site/upload
作者:Scott Konishi, Alan L. Yuille, James M. Coughlan, and Song Chun Zhu
摘要 -我们将边缘检测计算为统计推断。与基于模型的边缘检测标准方法不同,此统计边缘检测是数据驱动的。对于任何一组边缘检测过滤器(实现局部边缘提示),我们使用预先分割的图像来学习基于响应在边缘上还是边缘上进行评估的过滤器响应的概率分布。边缘检测公式化为通过对滤波器响应进行似然比测试指定的判别任务。这种方法强调了对图像背景(边缘)建模的必要性。我们非参数地表示条件概率分布,并举例说明了100个(Sowerby)和50个(SouthFlorida)图像的两个不同数据集。利用它们的联合分布组合了包括色度和多尺度在内的多个边界。因此,该提示组合在统计意义上是最佳的。我们使用切尔诺夫信息和接收器操作员特征(ROC)曲线评估了不同视觉提示的有效性。这表明,当图像背景包含明显杂波时,我们的方法在定量上要比Canny边缘检测器更好。另外,它使我们能够确定不同边缘提示的有效性,并针对多级处理的优势,色度的使用以及不同检测器的相对有效性给出了定量措施。此外,我们表明我们可以在一个数据集上学习这些条件分布,并在不影响第二个数据集的实际情况的情况下,仅对性能稍作降低就可以使它们适应另一条件集。这表明我们的结果并非完全是特定于域的。
索引词-边缘检测,统计学习,性能分析,贝叶斯推理。
1 引言
边缘检测器,请参见[9],旨在检测和定位对象的边界(在本文中,我们将使用“ edge”作为对象边界或显着反照率变化的简写,请参见图1,以及图5和6的后续示例)。 7和8)。实际上,很明显边缘检测是一个不适定的问题。设计一种边缘检测器是不可能的,该边缘检测器将发现图像中的所有真实(即,物体边界和显着的反照率变化)边缘并且不对其他图像特征做出响应。检查真实图像,很明显,边缘检测器仅给出有关对象边界存在的模糊局部信息。

图1.典型的Sowerby图像(左上图)及其地面真值分割(右上图),使用Canny边缘检测器(左下图)和统计边缘检测(底部中图)进行分割。 统计边缘检测在纹理区域中具有较少的假阴性,并且在检测由纹理部分定义的边缘方面也更好。 相比之下,Canny检测器在某些边缘的精度上稍好一些。 还显示了对数似然比(右下图)。
大多数常规边缘检测器是通过假设边缘模型来设计的。例如,Canny [9]假设边缘是被加性高斯噪声破坏的阶跃函数。但是,正如已被广泛报道的[12],[1],[30],[39],[24],[35]一样,自然图像具有高度结构化的统计属性,通常与当前边缘所做的假设不一致探测器。因此,将边缘检测公式化为统计推断是有意义的,其中边缘的可检测性不仅取决于边缘上的滤镜的统计信息,还取决于边缘上的滤镜的统计信息(即,背景图像的杂波)。这些边缘和背景统计信息可能是特定于域的,边缘检测应将此考虑在内。 (一种替代方法是在不学习概率分布的情况下学习分类器[35],但我们显示有足够的数据来学习分布)。
为了实现统计边缘检测,我们利用地面真实性分割,请参见图1、7和8。在学习阶段,我们首先使用两个预先分段的数据集Sowerby和South Florida,以确定针对边缘检测过滤器响应的概率分布。边缘。然后可以使用对数似然比检验执行边缘检测,请参见[11]。 (此外,这些对数似然比,参见图1可以用作诸如蛇[18]和区域竞争[38]等公式中边缘强度[14]的局部度量)。我们使用标准滤波器,例如强度梯度,高斯的拉普拉斯算子和定向滤波器对的滤波器组(例如Gabor滤波器)。为了组合不同的边缘提示,我们将边缘滤镜指定为矢量值,并具有与不同提示对应的分量(例如灰度,色度和多尺度)。换句话说,我们使用不同边缘提示的联合分布(这是组合它们的最佳方法)。
概率分布由多维直方图非参数表示。箱边界被自适应地确定以便减少所需箱的总数。这是必要的,以确保我们有足够的数据来学习概率分布并防止过度学习[34]。我们使用交叉验证[29]来检查过度学习。另外,有时我们使用决策树[29]来进一步减少所需的bin数量。
在我们的评估阶段,我们通过两个标准来确定边缘检测滤波器的有效性:1)通过评估Chernoff信息[11]和2)通过确定接收器工作特性(ROC)曲线[15]。切尔诺夫信息自然产生于Yuille和Coughlan [36]的理论研究中,用于确定航空影像中道路的可检测性[14]。 Bowyer等人已经使用了ROC曲线。以经验评估南佛罗里达数据集上标准边缘检测器的性能[7],[31],[8]。因此,我们可以使用ROC曲线将统计边缘检测的性能与更多标准边缘检测器进行比较。此外,我们使用ROC曲线下的面积和贝叶斯风险。
大多数实用的边缘检测器(例如Canny [9])使用后处理技术,例如非最大抑制和磁滞。因此,我们扩展了统计边缘检测以合并空间分组提示。这些分组提示也可以从我们的图像数据集中获得,毫不奇怪,它们显示出非最大抑制和滞后的类似物。
我们的结果表明,在Sowerby数据集上进行评估时,统计边缘检测的性能明显优于Canny边缘检测器[9],请参见图16。在南佛罗里达州的数据集上,统计边缘检测的性能与Canny边缘检测器相当,并且是最好的。 Bowyer等评估的其他边缘检测器。 [7],[8]。我们的结果还表明,与南佛罗里达数据集相比,检测Sowerby数据集中的边缘要困难得多。这是因为Sowerby图像中存在更多“杂波”,这会导致边缘检测器报告误报,请参见图1。我们假设边缘检测器不应报告杂乱和纹理区域中的边缘。总体而言,Sowerby数据集更具挑战性,并且(可以说)更具真实性。
我们也可以只对性能进行很小的调整就可以调整Sowerby和South Florida数据集之间的概率分布。换句话说,我们可以在南佛罗里达州进行高质量的分割,而无需地面事实(同样在Sowerby上)。此外,我们的自适应成功还表明,相对于地面真实性,图像统计数据是可靠的。对Sowerby和South Florida数据集的检查表明,事实的确定有很大不同,请参阅第3.1节。如果统计数据对基本事实非常敏感,那么就不可能在两个数据集之间进行调整。
我们的方法是对视觉算法的经验性能分析的最新工作的补充[6]。我们的工作最初受到Geman和Jedynak [14]的启发,他们学习了航空影像中公路上和公路下过滤器的统计响应。我们还受到Balboa和Grzywacz [2],[3],[4]的工作的影响,他们测量了两个图像域中遮挡边界上下的对比边缘统计量,他们认为这对应于感受野性质的差异在两种不同环境中对动物的视网膜进行分析,并提出了另一种适应方法[16]。最近的一种学习方法[27]与我们的方法大不相同,它利用具有高水平反馈的强化学习。最近,Sullivan等人。 [33]在“贝叶斯相关性”研究中学习了图像背景的统计数据。
本文的结构如下:在第二部分中,我们描述了边缘过滤器,两个评估标准以及如何表示和学习条件概率分布。第三部分使用两个评估标准给出了在两个数据集上的边缘检测过滤器的结果。在第4节中,我们描述了如何学习空间分组,作为非最大抑制和磁滞的类比。第5节表明,我们可以将概率分布从一个数据集调整为另一个数据集,这说明我们的结果并非纯粹是特定于数据集的,也不是过度依赖于数据集的基本事实。
2 代表,学习和评估边缘过滤器
统计边缘检测包括学习针对滤波器响应X的条件概率分布 和
和 ,条件是根据对滤波器是 在边缘上还是在边缘外 进行评估。然后,我们可以使用对数似然比检验
,条件是根据对滤波器是 在边缘上还是在边缘外 进行评估。然后,我们可以使用对数似然比检验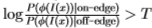 来确定图像 I(x)中的像素x 是否为边缘,其中T 是合适的阈值(在视觉上更令人愉悦的边缘图)但是,可以使用进一步的空间分组阶段来获得,请参见第4节)。根据Geman和Jedynak [14]的分析,对数似然比还可以用作边缘强度的度量,作为曲线检测器(如蛇)[18]或区域竞争[38]的输入。
来确定图像 I(x)中的像素x 是否为边缘,其中T 是合适的阈值(在视觉上更令人愉悦的边缘图)但是,可以使用进一步的空间分组阶段来获得,请参见第4节)。根据Geman和Jedynak [14]的分析,对数似然比还可以用作边缘强度的度量,作为曲线检测器(如蛇)[18]或区域竞争[38]的输入。
这要求我们指定一组边缘检测滤波器 ,请参阅第2.1节。我们使用性能标准评估不同边缘滤波器的有效性,请参阅第2.2节。这要求通过自适应非参数表示(例如直方图)表示条件概率分布,请参见第2.3节。性能标准还用于通过评估由不同可能表示形式引起的概率分布的有效性来确定自适应非参数表示形式。
,请参阅第2.1节。我们使用性能标准评估不同边缘滤波器的有效性,请参阅第2.2节。这要求通过自适应非参数表示(例如直方图)表示条件概率分布,请参见第2.3节。性能标准还用于通过评估由不同可能表示形式引起的概率分布的有效性来确定自适应非参数表示形式。
一旦选择了非参数表示,则学习概率分布将减少对数据集上的滤波器的评估(使用地面真值确定哪些像素在边缘上和边缘上)并计算每个bin中的响应数。
2.1 两个过滤器集
我们考虑两组边缘检测滤波器。 第一组包括标准边缘滤镜(由Nitzberg滤镜补充,事实证明非常有效)。 第二组包括定向滤镜库,部分受人类视觉系统生物学的启发。
2.1.1 第一个过滤器集
在本文中,我们通过微分(或差分)运算符指定滤镜 ,应用滤镜的比例以及应用滤镜的色带。 表1中显示了第一组中的滤镜。滤镜的尺寸是操作员的尺寸,比例尺数量和像带数量的乘积。 例如,过滤器编号。 表中的no. 2是应用于图像带Y 的三个比例的Laplacian
,应用滤镜的比例以及应用滤镜的色带。 表1中显示了第一组中的滤镜。滤镜的尺寸是操作员的尺寸,比例尺数量和像带数量的乘积。 例如,过滤器编号。 表中的no. 2是应用于图像带Y 的三个比例的Laplacian 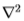 运算符,因此是三维滤波器。
运算符,因此是三维滤波器。
表1第一组中的12个过滤器
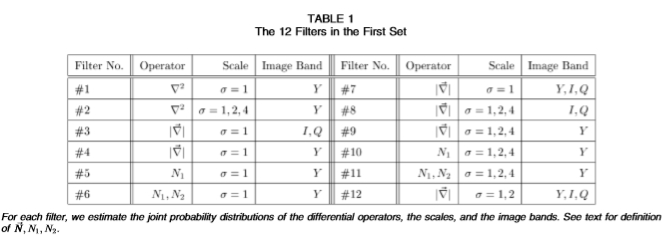
对于每个滤波器,我们估计微分算子,比例尺和像带的联合概率分布。 参见文本,了解N,N1,N2的定义。
对于第一个滤波器组,微分算子是图像梯度 的大小,Nitzberg算子
的大小,Nitzberg算子 [26]和Laplacian
[26]和Laplacian 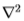 [25]。通过使用具有方差
[25]。通过使用具有方差 2的高斯滤波器对图像进行平滑处理,可以将它们应用于不同的比例
2的高斯滤波器对图像进行平滑处理,可以将它们应用于不同的比例 。 Sowerby有三个色带Y,I,Q,南佛罗里达有一个色带(即灰度)。更准确地说,梯度的模数和拉普拉斯算子由方程式指定
。 Sowerby有三个色带Y,I,Q,南佛罗里达有一个色带(即灰度)。更准确地说,梯度的模数和拉普拉斯算子由方程式指定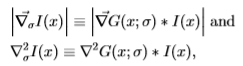
其中 * 表示卷积,而 G(x; )是由标准偏差
)是由标准偏差 参数化的空间尺度上的高斯。Nitzberg算子涉及计算矩阵
参数化的空间尺度上的高斯。Nitzberg算子涉及计算矩阵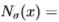
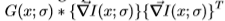 ,其中T 表示转置。换句话说,我们在比例尺
,其中T 表示转置。换句话说,我们在比例尺 处获取图像梯度,然后通过具有相同比例尺的高斯对它的外积求平均(我们发现在两个比例尺上使用相同的
处获取图像梯度,然后通过具有相同比例尺的高斯对它的外积求平均(我们发现在两个比例尺上使用相同的 值最有效)。输出是由两个特征值
值最有效)。输出是由两个特征值 组成的二维向量。该运算符对图像角敏感(请参见[5]中Harris的第4章,第16章),这有助于将纹理与边缘区分开,正如我们将在第3节中看到的那样 。
组成的二维向量。该运算符对图像角敏感(请参见[5]中Harris的第4章,第16章),这有助于将纹理与边缘区分开,正如我们将在第3节中看到的那样 。
我们的颜色表示是NTSC颜色空间的一种变体,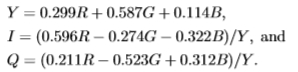
在此,Y被解释为灰度图像,I,Q为色度矢量。与NTSC不同,我们通过灰度对色度进行了归一化。这种归一化使我们能够检查与灰度无关的色度提示的有效性。重要的是要认识到色彩空间表示的选择相对不重要,因为我们使用联合分布来组合色彩提示。唯一重要的原因是因为我们根据一维分布(这确实取决于我们对颜色空间的选择)来确定容器边界。
人类视觉的生物学结合更多的务实动机,强烈建议应该以不同的比例来处理图像,参见[25]。在这种“尺度空间”方法中,并不总是很清楚如何最好地组合边缘探测器在不同尺度下给出的信息。如本文所述,在统计边缘检测中,最佳组合是通过使用不同比例的滤波器联合分布而自然产生的(取决于我们使用的量化程序)。
在本文的其余部分中,我们由操作员表示滤镜,应用滤镜的标度以及应用于滤镜的色带。例如,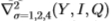 表示过滤器是高斯的拉普拉斯算子,以比例
表示过滤器是高斯的拉普拉斯算子,以比例 =1,2,4应用于三个色带Y,I,Q。该过滤器具有九个维度的矢量值。这些不同组合的有效性在3.2.1节中显示。
=1,2,4应用于三个色带Y,I,Q。该过滤器具有九个维度的矢量值。这些不同组合的有效性在3.2.1节中显示。
2.1.2 第二个过滤器集
第二个滤波器组是一组定向调整的对称(偶数)和反对称(奇数)滤波器对。据称,视觉皮层使用这种类型的滤波器组,并且可以通过所谓的能量滤波器来检测边缘,所述能量滤波器将偶数和奇数滤波器对的平方相加。在计算机视觉文献中,Perona和Malik [28]提倡使用这种类型的滤波器对,因为它们对阶跃边缘(由于奇数滤波器)和对脊边缘(由于偶数滤波器)都具有敏感性。另见[17]。
在本节中,我们考虑两种类型的滤波器对。首先,我们考虑偶数和奇数Gabor滤波器对,其中偶数滤波器是余弦Gabor(经偏移以消除DC项),而奇数滤波器是具有相同方向和频率的正弦Gabor。我们将取向角量化为四个值。对于每个角度,滤镜都可以在角度方向和正交方向上与一个分量分开。 Gabor滤波器在正交方向上的横截面由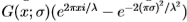 的实部和虚部给出,其中
的实部和虚部给出,其中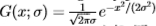 。出于生物学考虑,我们设置
。出于生物学考虑,我们设置 =
= /2。Gabor在角度的方向上具有G(x;
/2。Gabor在角度的方向上具有G(x;
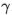 )的横截面,其中
)的横截面,其中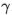 是纵横比。。总而言之,每个Gabor滤波器都由角度
是纵横比。。总而言之,每个Gabor滤波器都由角度 ,波长
,波长 和纵横比
和纵横比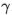 来描述。
来描述。
Gabor滤波器的一个众所周知的局限性是由于其高频响应,它们趋向于“靠近”边缘的趋势。这激发了我们的第二个选择,其中滤波器对也以一组量化的角度出现。与角度正交的横截面是高斯 的二阶导数,其希尔伯特变换定义为
的二阶导数,其希尔伯特变换定义为

角度方向上的横截面也是G(x;
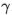 )。为了与Gabor滤光片进行比较,我们定义了有效波长
)。为了与Gabor滤光片进行比较,我们定义了有效波长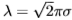 。我们将它们称为希尔伯特变换滤光片。 (Perona和Malik建议使用希尔伯特变换对[28])。 这些希尔伯特变换对以六个方向(等距)运行。
。我们将它们称为希尔伯特变换滤光片。 (Perona和Malik建议使用希尔伯特变换对[28])。 这些希尔伯特变换对以六个方向(等距)运行。
为了表示组合滤波器对的不同方法,我们使用以下符号: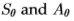 分别表示方向
分别表示方向 上的对称和反对称滤波器,其中X量化为四个到六个值(选择以跨越方向空间)。 我们可以用单个(高维)滤波器
上的对称和反对称滤波器,其中X量化为四个到六个值(选择以跨越方向空间)。 我们可以用单个(高维)滤波器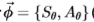 (取决于角度数,维数是8或12)来表示滤波器组的输出。 或者,有四个或六个“能量”滤波器
(取决于角度数,维数是8或12)来表示滤波器组的输出。 或者,有四个或六个“能量”滤波器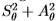 调整到方向
调整到方向 。此外,我们测试了在角度方向
。此外,我们测试了在角度方向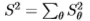 和
和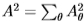 上平均的滤波器以及二维滤波器
上平均的滤波器以及二维滤波器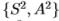 。 最后,有一维滤波器
。 最后,有一维滤波器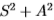 。 我们的结果(请参阅第3.2.2节)显示,
。 我们的结果(请参阅第3.2.2节)显示,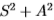 提供了令人惊讶的信息量。
提供了令人惊讶的信息量。
2.2 绩效标准
我们使用两个性能标准。第一个标准是Chernoff信息[11],请参见2.2.1节。这是确定两个分布中哪个分布会生成一组样本的简便性的度量(必须从同一分布中采样该集合的所有成员)。在理论研究中[36]出现了在航空影像中检测道路的困难[14]。第二个标准是第2.2.2节的接收器工作特性(ROC)曲线[15]。
可从ROC曲线获得两个额外的度量。第一个是ROC曲线下的面积,可以显示等于1减去2替代强制选择任务的错误率[15]。第二个度量是贝叶斯风险[29],也可以直接从ROC曲线中获得(具有相同的边缘和离边先验概率)。出乎意料的是,对于本文中的边缘检测器滤波器,在ROC曲线下方的区域和Chernoff信息之间存在一个简单的经验一对一映射,请参见3.3.2节。此外,经验ROC曲线的性质表明,可以通过ROC曲线下的面积来近似地对其进行唯一表征,请参见3.3.2节。因此,ROC曲线也与Chernoff信息直接相关。
两种性能标准都是统计可辨别性的度量,其中使用对数似然比检验进行区分[11]。 因此,两种性能指标仅取决于对数似然比的诱导分布

这些感应分布是一维的,经验上近似是具有相同方差的高斯分布。 当理解切尔诺夫曲线和ROC曲线之间的经验关系时,这一点很重要。
请注意,这两个标准都是根据概率推断得出的[11],[15]。 将它们应用于不是以概率术语表述的边缘检测器不是简单的。 例如,ROC曲线假定存在可以更改的一维参数。 对于统计边缘检测,此参数对应于用于边缘检测的阈值。 但是,常规的边缘检测器可以包含几个可调参数。 例如,Canny检测器[9]包含三个可调参数(一个标度和两个阈值)。 Bowyer等。 [7],[8]通过选择这些参数的最佳选择来获得ROC曲线。
2.2.1 Chernoff信息
我们的第一个性能指标是Chernoff信息[11],其动力来自以下问题:假设我们希望确定一组样本是边缘的还是边缘的。 当确定是否要“分组”一组图像像素以形成连续边缘路径时,此任务很重要。 在分析Geman和Jedynak曲线检测理论时,切尔诺夫信息和密切相关的Bhattacharyya系数与Yuille和Coughlan [36]确定的阶跃参数直接相关[14]。 在此理论中,边缘上和边缘外的滤波器响应的概率分布之间的Chernoff信息越大,则阶数参数越大,检测曲线越容易。
令 为在位置x1; ...; xN处边缘检测器响应的独立样本序列。 使用Neyman-Pearson引理[11],用于确定样本是否来自
为在位置x1; ...; xN处边缘检测器响应的独立样本序列。 使用Neyman-Pearson引理[11],用于确定样本是否来自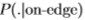 或
或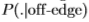 的最佳检验(例如,最大似然检验)仅取决于对数似然比,
的最佳检验(例如,最大似然检验)仅取决于对数似然比,
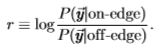
根据独立性的假设,这减少到

对数似然比越大,则测量样本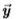 越有可能来自边缘分布而不是边缘分布(如果对数似然比为零,则边缘和边缘的可能性均相等)。 可以证明[11],对于足够大的N,此测试的预期错误率呈指数下降
越有可能来自边缘分布而不是边缘分布(如果对数似然比为零,则边缘和边缘的可能性均相等)。 可以证明[11],对于足够大的N,此测试的预期错误率呈指数下降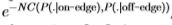 ,其中C(p,q)是两个概率分布p和q之间的切尔诺夫信息[11],定义为:
,其中C(p,q)是两个概率分布p和q之间的切尔诺夫信息[11],定义为:
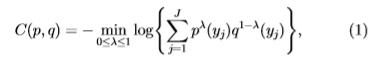
其中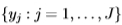 是定义分布的变量(在本文中,每个yi对应于直方图bin)。 Bhattacharyya系数是一个密切相关的量:
是定义分布的变量(在本文中,每个yi对应于直方图bin)。 Bhattacharyya系数是一个密切相关的量:

但是,根据经验,我们发现边缘检测滤波器的切尔诺夫信息几乎始终对应于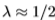 的值,请参见第3节。因此,在我们的应用领域中,切尔诺夫信息和Bhattacharyya系数给出的值非常相似。 唯一不会发生这种情况的情况是数据太少并且模型开始过度学习。 但是,在一般情况下,对于任何p,q都是
的值,请参见第3节。因此,在我们的应用领域中,切尔诺夫信息和Bhattacharyya系数给出的值非常相似。 唯一不会发生这种情况的情况是数据太少并且模型开始过度学习。 但是,在一般情况下,对于任何p,q都是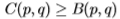 (因为Chernoff信息选择
(因为Chernoff信息选择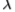 以使
以使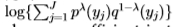 相对于
相对于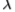 最小,而Bhattacharyya系数仅设置
最小,而Bhattacharyya系数仅设置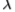 = 1/2)。
= 1/2)。
为了说明切尔诺夫信息,我们首先针对两个具有方差 2和均值u1,u2的单变量高斯计算该信息。 它变为X个nat(1个nat等于log2e位),对于特殊情况,当X时,切尔诺夫信息等于0.125个nat。
2和均值u1,u2的单变量高斯计算该信息。 它变为X个nat(1个nat等于log2e位),对于特殊情况,当X时,切尔诺夫信息等于0.125个nat。
为了说明切尔诺夫信息,我们首先为两个具有方差 2和均值u1,u2的单变量高斯计算它。 它变为
2和均值u1,u2的单变量高斯计算它。 它变为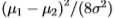 个nat(1个nat等于log2 e位),对于特殊情况,当u2-u1=
个nat(1个nat等于log2 e位),对于特殊情况,当u2-u1= 时,切尔诺夫信息等于0.125个nat。
时,切尔诺夫信息等于0.125个nat。
2.2.2 接收器工作特性曲线
我们还使用ROC曲线[15]评估边缘检测滤波器,以对单个像素进行分类。 根据对数似然比,将像素分为“边缘*”或“边缘*”
分别高于或低于阈值T。 每个阈值T都会在ROC曲线上产生一个点,对应于正确响应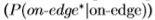 和误报
和误报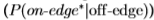 的比例,见图5。
的比例,见图5。
我们使用可以从ROC曲线得出的两个附加度量:1)ROC曲线下的面积(该数字减去2替代性强制选择任务(2AFC)的错误率)和2)给出的贝叶斯风险
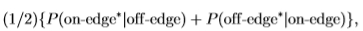
如果像素x被分类为“边缘*”,如果

否则为“边缘*”。
2.3 两个非参数概率表示
我们将考虑两种非参数方式来表示概率分布。第一种使用多维直方图,并为每个维度(每个视觉提示一个维度)自适应选择bin边界。此表示使用的箱的数量随视觉提示的数量呈指数增加。学习这样的分布需要大量的训练数据,以避免过度学习[34],当我们没有足够的数据来准确地学习概率分布时(即,我们可以记住分布,但是不能从它们推广到新数据) )。这激发了我们的第二种表示方法,它使用决策树[29]选择最有助于区分的那些bin边界切口。这种表示使我们能够学习高维滤波器的分布。
我们使用交叉验证[29]来确定是否发生了过度学习。此过程了解数据集一部分的分布,并通过评估其余部分的分布来检查一致性。例如,假设我们尝试学习一个九维过滤器的分布,每个维度有六个容器(即总共69个容器)。然后交叉验证表明我们无法准确地学习分布,请参见图6。实际上,简单的线索通常足以告诉我们是否发生了过度学习。首先,仅当bin的数量等于或大于数据点的数量时,才会发生过度学习。其次,当发生过度学习时,我们的绩效标准会给出可疑的大数值。
自适应装箱和决策树过程使用性能度量来确定箱边界和决策割据的良好选择。这些性能度量,Chernoff信息和接收器操作特性(ROC)曲线在前面的第2.2节中进行了描述。
2.3.1 具有自适应分箱的多维直方图
回想一下,任何边缘提示(或提示的组合)都由运算符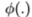 表示,该运算符
表示,该运算符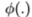 可以是具有标量或矢量值输出的线性或非线性滤波器。 例如,一种可能性是标量滤波器
可以是具有标量或矢量值输出的线性或非线性滤波器。 例如,一种可能性是标量滤波器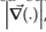 参见其他滤波器的2.1节。
参见其他滤波器的2.1节。
选择了边缘算子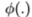 后,我们必须量化其响应值。 这涉及选择可能的响应
后,我们必须量化其响应值。 这涉及选择可能的响应 的有限集合。算子的有效性将取决于此量化方案,因此必须注意确定量化是否可靠且接近最佳。
的有限集合。算子的有效性将取决于此量化方案,因此必须注意确定量化是否可靠且接近最佳。
我们说明了对滤波器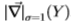 的量化。对于一维滤波器,始终有足够的数据来学习
的量化。对于一维滤波器,始终有足够的数据来学习 和
和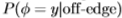 具有256个bin的直方图。图2表明,
具有256个bin的直方图。图2表明,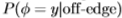 的概率分布在y = 0附近强烈峰值(即,则图像梯度倾向于远离边缘变小),而
的概率分布在y = 0附近强烈峰值(即,则图像梯度倾向于远离边缘变小),而 的峰值出现在较大的y=0值处(即,图像梯度在边缘处很可能非零)。我们计算这两个分布之间的Chernoff信息,以为我们区分这些分布的程度提供上限。然后,我们选择以贪心方式最大化Chernoff信息的bin边界,并计算Chernoff信息如何随着bin数量的增加而朝着上限增加。这在图2中进行了绘制,并显示切尔诺夫信息仅用少量的仓即可迅速达到其渐近值。显然,对于滤波器的每个维度,仅使用六个自适应bin即可提取大多数可靠信息(这种自适应是针对整个数据集而不是针对每个单独的图像执行的)。
的峰值出现在较大的y=0值处(即,图像梯度在边缘处很可能非零)。我们计算这两个分布之间的Chernoff信息,以为我们区分这些分布的程度提供上限。然后,我们选择以贪心方式最大化Chernoff信息的bin边界,并计算Chernoff信息如何随着bin数量的增加而朝着上限增加。这在图2中进行了绘制,并显示切尔诺夫信息仅用少量的仓即可迅速达到其渐近值。显然,对于滤波器的每个维度,仅使用六个自适应bin即可提取大多数可靠信息(这种自适应是针对整个数据集而不是针对每个单独的图像执行的)。
对于高维滤波器,我们仅使用矩形容器,其边界由一维边际给定。

图2:左图:Y = 1时Y上梯度滤波器幅度的边际分布(根据Sowerby数据集评估)。 垂直轴标记概率密度,水平轴标记滤波器响应。 深色线表示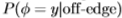 ,虚线表示
,虚线表示 。垂直虚线表示自适应选择的条带边界的位置。 右图:切尔诺夫信息随分箱数的变化迅速达到渐近值。
。垂直虚线表示自适应选择的条带边界的位置。 右图:切尔诺夫信息随分箱数的变化迅速达到渐近值。
2.3.2 决策树表示
多维直方图表示的主要缺点是,使用的bin的数量随边缘滤波器的维数呈指数增长,因此所需的训练数据量也呈指数增长。 这就限制了我们可以使用的边缘滤波器的维数。
决策树方法给出了更紧凑的表示。 此外,它还允许我们通过调整表示的大小来学习发生过度学习的情况下的概率,请参见第2.3.3节。
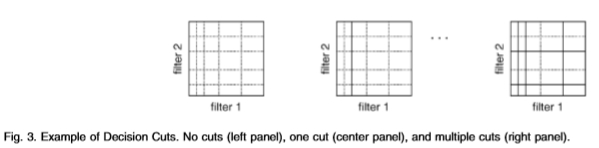
图3:决策削减示例 无切口(左侧面板),一个切口(中央面板)和多个切口(右侧面板)。
决策树过程包括在任何一维滤波器轴上自适应选择切点,以便最大化Chernoff信息,请参见图3。我们使用贪婪算法选择最佳的bin选择。 就是说,我们找到了第k个切入点,方法是添加bin边界,该切入点边界在给定最佳k-1切入的情况下最大化Chernoff信息。 更准确地说,假设我们有一个M维滤波器,该滤波器在M处具有一维bin边界(其中n是一维直方图中使用的bin数-在本文中通常为n = 6)。 过滤器的分布为X。在没有削减的情况下,两个分布A和B当然是无法区分的。 然后,我们找到最佳的裁切yim,它使两个分布之间的Chernoff信息最大化。 然后,我们选择第二个最佳切割(给定第一个最佳切割),依此类推。 这是一种表示概率分布的替代方法,其中框的数量以2k为界,其中k是切割的数量。
决策树过程包括在任何一维滤波器轴上自适应选择切点,以便最大化Chernoff信息,请参见图3。我们使用贪婪算法选择最佳的bin选择。 就是说,我们通过添加bin边界找到第k个切入点,在最佳k-1切入的情况下,该切入边界使Chernoff信息最大化。 更准确地说,假设我们有一个M维滤波器,该滤波器在 1,...,n, m= 1, ..., M}处具有一维bin边界(其中n是一维直方图中使用的bin数-在本文中通常为n = 6)。 过滤器的分布为
1,...,n, m= 1, ..., M}处具有一维bin边界(其中n是一维直方图中使用的bin数-在本文中通常为n = 6)。 过滤器的分布为 和
和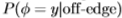 。在没有削减的情况下,两个分布
。在没有削减的情况下,两个分布 和
和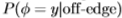 当然是无法区分的。 然后,我们找到最佳的裁切yim,它使两个分布之间的Chernoff信息最大化。 然后,我们选择第二个最佳切割(给定第一个最佳切割),依此类推。 这是一种表示概率分布的替代方法,其中框的数量以2k为界,其中k是切割的数量。
当然是无法区分的。 然后,我们找到最佳的裁切yim,它使两个分布之间的Chernoff信息最大化。 然后,我们选择第二个最佳切割(给定第一个最佳切割),依此类推。 这是一种表示概率分布的替代方法,其中框的数量以2k为界,其中k是切割的数量。
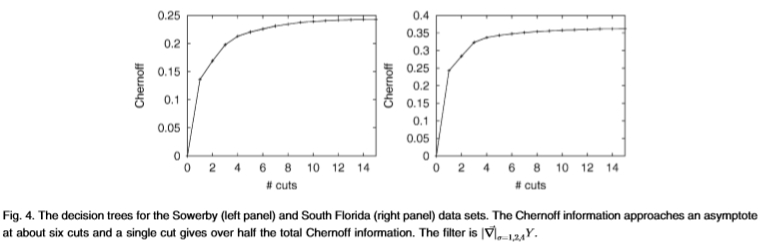
图4:Sowerby(左图)和South Florida(右图)数据集的决策树。 Chernoff信息在大约六次切入时接近渐近线,而一次切入则提供了总Chernoff信息的一半以上。 过滤器是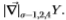 。
。
决策树过程(参见图4)显示,通常可以使用很少的决策切入获得大量信息内容。例如,通过六次剪切(即n = 6),我们通常会获得全部Chernoff信息的80%至90%。使用最多26个= 64箱而不是69 = 10,077,696箱,可以很好地近似完整的直方图。实际上,单次剪切(即使用单个过滤器的边际分布)通常会产生总Chernoff信息的40%至50%。这表明添加到目前为止我们已经考虑过的类型的额外过滤器以及二进制边缘和边缘边缘决策任务的收益递减。
2.3.3 过度学习,交叉验证和决策树
决策树过程还使我们能够了解发生过度学习的高维滤波器的概率分布。对于每个决策削减次数,我们使用交叉验证来检验是否过度概括(使用Chernoff或ROC作为绩效标准)。这使我们能够确定最大决策数量,同时防止过度学习。边缘像素和边缘像素的数量在Sowerby上为(2.35 * 106,34.3 * 106),在南佛罗里达州为(4.31 * 105,12.1 * 106)。
为了进行交叉验证,我们将数据集(Sowerby或South Florida)随机分为两组,即set0和set1。 我们了解到这两个数据集上的分布是决策削减次数的函数。 然后,我们通过计算set1上的set0和set0上的set1来计算两个数据集内的Chernoff信息和/或ROC曲线(通过评估set0上的set0和set1上的set1)以及跨越这两个数据集。
例如,我们可以计算过滤器 的ROC曲线。该过滤器是9维的,因此具有69 = 10.077696 * 106个bin,太大,无法可靠地学习,因为它的数量级与数量x相同。 Sowerby数据集中的边缘和边缘像素。如果我们尝试使用多尺度直方图来学习分布,则组内ROC曲线与组间ROC不一致,因此,我们会过度学习,请参见图5的左图。但是,如果我们使用决策用20个切口的树表示,那么所有ROC曲线都是一致的,请参见图5(右图),并且没有过度学习。决策树过程将bin的数量减少到13.8 * 103,这远远小于边缘和边缘Sowerby像素的数量。
的ROC曲线。该过滤器是9维的,因此具有69 = 10.077696 * 106个bin,太大,无法可靠地学习,因为它的数量级与数量x相同。 Sowerby数据集中的边缘和边缘像素。如果我们尝试使用多尺度直方图来学习分布,则组内ROC曲线与组间ROC不一致,因此,我们会过度学习,请参见图5的左图。但是,如果我们使用决策用20个切口的树表示,那么所有ROC曲线都是一致的,请参见图5(右图),并且没有过度学习。决策树过程将bin的数量减少到13.8 * 103,这远远小于边缘和边缘Sowerby像素的数量。
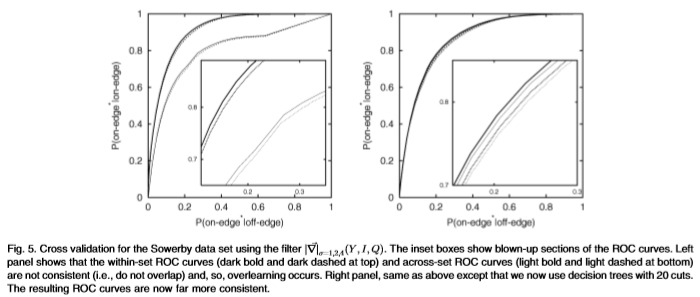
图5:使用过滤器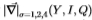 对Sowerby数据集进行交叉验证。插图框显示了ROC曲线的放大部分。 左图显示了内部ROC曲线(顶部为粗黑线和深色虚线)和跨组ROC曲线(底部为浅黑体线和浅虚线)不一致(即不重叠),因此发生了过度学习。 右面板与上面相同,除了我们现在使用具有20条削减的决策树。 现在生成的ROC曲线更加一致。
对Sowerby数据集进行交叉验证。插图框显示了ROC曲线的放大部分。 左图显示了内部ROC曲线(顶部为粗黑线和深色虚线)和跨组ROC曲线(底部为浅黑体线和浅虚线)不一致(即不重叠),因此发生了过度学习。 右面板与上面相同,除了我们现在使用具有20条削减的决策树。 现在生成的ROC曲线更加一致。
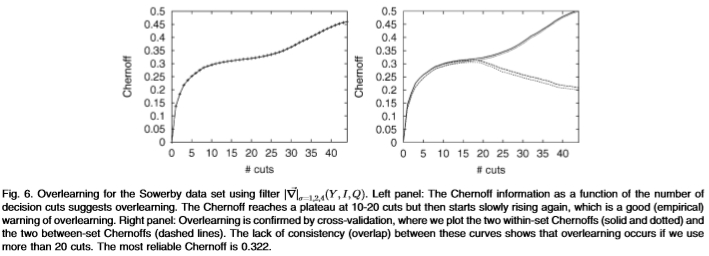
图6:使用过滤器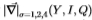 对Sowerby数据集的过度学习。左图:切尔诺夫信息作为决策切入次数的函数表明过度学习。 切尔诺夫(Chernoff)在10到20割时达到平稳状态,然后又开始缓慢上升,这是过度学习的良好(经验)警告。 右图:通过交叉验证确认了过度学习,在该图中我们绘制了两个内部切尔诺夫(实线和点线)和两个内部切尔诺夫(虚线)。 这些曲线之间缺乏一致性(重叠),这表明如果我们使用20多个剪切,则会发生过度学习。 最可靠的切尔诺夫为0.322。
对Sowerby数据集的过度学习。左图:切尔诺夫信息作为决策切入次数的函数表明过度学习。 切尔诺夫(Chernoff)在10到20割时达到平稳状态,然后又开始缓慢上升,这是过度学习的良好(经验)警告。 右图:通过交叉验证确认了过度学习,在该图中我们绘制了两个内部切尔诺夫(实线和点线)和两个内部切尔诺夫(虚线)。 这些曲线之间缺乏一致性(重叠),这表明如果我们使用20多个剪切,则会发生过度学习。 最可靠的切尔诺夫为0.322。
或者,我们可以使用Chernoff信息检查过度学习。在图6的左侧面板中,我们绘制了切尔诺夫信息如何随切割次数增加的情况。观察到切尔诺夫(Chernoff)在大约10个切割处迅速增加到一个平稳的水平,但随后在20个切割处又开始上升。根据我们的经验,这种从高原的崛起始终是过度学习的标志。为了验证这一点,请在图6的右面板中观察交叉验证的结果。从高原的上升可以用作启发式检查,以检查是否发生了过度学习。
通过这种技术,与自适应直方图方法相比,我们可以使用更高维的滤波器。当使用定向滤波器组时,这特别有用,请参见第2.1.2节。滤波器组需要大量数据,因为它们涉及以四个或六个方向运行滤波器对。例如,如果我们使用四个方向,则滤波器组是八维的,并且需要1.679616 * 106个bin,太大,无法在South Florida数据集上学习。但是,决策树方法将bin的数量减少到104个,并防止了过度学习,请参见图13。
3 边缘识别结果
现在我们描述实验结果,其目的是确定给定像素是在边缘上还是边缘上。
我们在Sowerby和South Florida数据集上评估我们的方法。 这些数据集在重要方面有所不同,我们将在第3.1节中进行介绍。 然后,我们使用第3.2节中的Chernoff信息和第3.3节中的ROC曲线评估线索。 在3.3.2节中显示,两个标准给出的结果相似。
3.1 两个数据集
Sowerby数据集包含一百个预先分段的彩色图像。南佛罗里达州的数据集包含五十个灰度图像。这些数据集的不同之处在于图像的性质以及用于构造分割的方法(地面真实情况)。

图7:第一行:Sowerby数据集中的四幅典型图像,其中包含各种城市和乡村场景(原始图像为彩色)。 下一行:Sowerby图像数据集随附的地面真相分割。 基本事实并不完美; 一些边缘缺失,一些边缘宽几个像素。

图8:左图:南佛罗里达数据集的四幅典型图像,主要包括室内图像和人造物体。 右面板:南佛罗里达图像数据集提供的地面真相分割。
Sowerby图像(见图7)是在英格兰拍摄的室外图像,全部包含道路或赛道。图像背景包含大量植被(例如草,荆棘,树木),与图像中的纹理相对应。地面真实情况包括边缘不是很清晰或轮廓不清。例如,它们包括人行道与周围小草之间的边界。总体而言,数据集对于边缘检测器,尤其是对于仅使用灰度信息的检测器来说,是一个挑战。相反,南佛罗里达州的数据集(见图8)主要由室内图像组成。背景纹理很少。而且,地面真实边缘通常在视觉上是显着的并且在空间上是局部的(例如,仅一个像素宽)。
我们认为,在南佛罗里达数据集中正确检测边缘比在Sowerby中容易得多。 边缘更清晰,背景统计信息也更简单(由于缺少纹理)。 这些假设由本节其余部分的实验结果证实。
两个数据集中的基本事实显然是不同地创建的,请参见图7和8。 如图7和8所示。例如,南佛罗里达州的边缘较薄且局部很好。 相反,Sowerby边缘较厚(例如,通常两个像素宽)。 此外,南佛罗里达州的图像具有3值的地面真相,而索尔比图像具有2值。 对于南佛罗里达州,这三个值对应于三组:1)边缘,2)背景以及3)靠近边缘和背景中某些纹理区域的像素。 相反,Sowerby图像像素被标记为边缘或非边缘。 在我们的实验中,我们总是将南佛罗里达像素重新分类为边缘或非边缘(即,非边缘集是集合“ 1”和“ 2”的并集)。
Sowerby集中的五张图像(一百零四张)的边缘贴图质量很差,因此我们拒绝了。这些图像是06-36、10-19、13-10、13-13和14-22。
对于我们而言,拥有两个数据集非常有用,这两个数据集的统计量和地面真理的标准都不同。首先,如第5节所述,我们能够学习一个数据集的统计信息,然后将它们改编为另一个数据集,而只损失很小的性能。这表明统计边缘检测对于地面真实情况中的错误具有鲁棒性(因为如果边缘统计数据对两个数据集中使用的完全不同的地面真实条件非常敏感,则不可能达到此适应水平。其次,在(较轻松的)南佛罗里达数据集上,统计边缘检测仅比标准边缘检测器提供更好的结果(通过贝叶斯风险评估,请参阅第3.3.2节)。但是,统计边缘检测在(较困难的)Sowerby数据集上表现更好。参见图。 1和17进行视觉比较,然后在图16中比较Canny检测器和统计边缘检测的ROC结果。
3.2 使用Chernoff信息的结果
我们在第3.2.1节中显示了第一组过滤器的结果,在第3.2.2节中显示了第二组过滤器的结果。
为了校准单个线索的Chernoff信息,对于Geman和Jedynak道路跟踪应用程序,我们将其估计为0:22。 回想一下,当两个均值之差等于方差时,两个单变量高斯等于0.125。 这些设定了基准,并且如我们将显示的,通过组合线索,我们可以获得更高的Chernoff信息。
要校准多维过滤器的切尔诺夫信息,我们需要知道它如何随维数变化。 它可以保证永远不会减少,但原则上可以任意增加[11]。
例如,考虑两个分布p(i,j)=1/n2(其中i=1,...,n和 j=1,...,n),和q(i,j)=(1/n) 。然后,两个分布在i或j上的边际分布都相同,因此切尔诺夫信息和Bhattacharyya系数对于边际为零。 但是,p和q之间的Chernoff信息和Bhattacharyya系数分别为(1/2)logn。
。然后,两个分布在i或j上的边际分布都相同,因此切尔诺夫信息和Bhattacharyya系数对于边际为零。 但是,p和q之间的Chernoff信息和Bhattacharyya系数分别为(1/2)logn。
如果我们组合两个独立的线索,那么Chernoff信息将小于或等于每个线索的Chernoff信息之和。 但是,根据经验,我们总是发现Chernoff信息大约等于Bhattacharyya系数(即
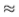 0.5,请参阅第2.2.1节)。 如果将两个独立的边缘线索组合在一起,那么它们的Bhattacharyya系数将简单地相加[11]。 因此,如果提示是独立的,我们预计切尔诺夫将增加。
0.5,请参阅第2.2.1节)。 如果将两个独立的边缘线索组合在一起,那么它们的Bhattacharyya系数将简单地相加[11]。 因此,如果提示是独立的,我们预计切尔诺夫将增加。
在实践中,我们发现两个耦合线索的切尔诺夫信息和Bhattacharyya系数通常比单个线索的总和小得多,请参阅第3节,因此我们得出结论:线索很少独立。
3.2.1 第一组过滤器的结果
现在,我们在一系列过滤器上显示结果,请参见表1。回顾2.1节,基本成分是:1)三个微分算子(请参见下文),2)三种不同的颜色(图像带Y,I,Q) ;以及3)通过将图像与高斯进行卷积而得到的三个比例,比例为  = 1,2,4像素。
= 1,2,4像素。

图9:索尔比和南佛罗里达的切尔诺夫斯。 边缘检测器的运算符由(N1,N2)的星形标记,对于N1的十字形标记,对于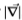 的三角形标记以及对于
的三角形标记以及对于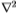 的菱形标记。 最左侧的三个面板分别为Sowerby绘制了全色,灰度和色度的Chernoff信息。 最右边的图是切尔诺夫(Chernoff)为南佛罗里达州绘制的灰度图。 横轴表示过滤器刻度(
的菱形标记。 最左侧的三个面板分别为Sowerby绘制了全色,灰度和色度的Chernoff信息。 最右边的图是切尔诺夫(Chernoff)为南佛罗里达州绘制的灰度图。 横轴表示过滤器刻度( = 1、2、4)。 不需要决策树。
= 1、2、4)。 不需要决策树。
我们的第一个结果(参见图9)比较了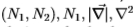 的滤镜性能,这些滤镜使用了不同比例,不同色带选择以及Sowerby和South Florida的滤镜。前两个面板说明了颜色优于灰度的优点。 (使用颜色进行边缘检测的优势有时在计算机视觉社区中受到质疑)。有趣的是,色度提示(已排除了灰度)在大范围内最有效,请参阅右中间面板。这与生物视觉很好地对应(对于生物视觉而言,色度滤镜的空间比例往往比灰度滤镜的空间比例大)。左中和右中面板显示,在南佛罗里达州检测边缘要比在Sowerby中检测边缘容易。此外,图9示出了Sowerby边缘在大尺度上最容易检测,而南佛罗里达边缘在低尺度上最容易检测(即,南佛罗里达边缘被急剧地定位)。
的滤镜性能,这些滤镜使用了不同比例,不同色带选择以及Sowerby和South Florida的滤镜。前两个面板说明了颜色优于灰度的优点。 (使用颜色进行边缘检测的优势有时在计算机视觉社区中受到质疑)。有趣的是,色度提示(已排除了灰度)在大范围内最有效,请参阅右中间面板。这与生物视觉很好地对应(对于生物视觉而言,色度滤镜的空间比例往往比灰度滤镜的空间比例大)。左中和右中面板显示,在南佛罗里达州检测边缘要比在Sowerby中检测边缘容易。此外,图9示出了Sowerby边缘在大尺度上最容易检测,而南佛罗里达边缘在低尺度上最容易检测(即,南佛罗里达边缘被急剧地定位)。
Nitzberg滤镜(N1,N2)很不错,因为它可以区分边缘和纹理。纹理被视为具有两个较大特征值的“角”。相比之下,在规则边缘只有一个特征值很大。但是,这意味着Nitzberg滤镜经常将真实的边角视为纹理,因此将其分类为边缘。

图10:使用多尺度滤波器的优势。 切尔诺夫信息的显示如下:1比例为 = 1,{1,2}的滤波器比例为
= 1,{1,2}的滤波器比例为 = {1,2}和{1,2,4}的耦合滤波器比例为
= {1,2}和{1,2,4}的耦合滤波器比例为 ={1,2,4}的耦合滤波器。随着我们添加更大比例的滤波器,切尔诺夫总是增加。 约定如图9所示。 当应用过滤器
={1,2,4}的耦合滤波器。随着我们添加更大比例的滤波器,切尔诺夫总是增加。 约定如图9所示。 当应用过滤器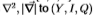 标度
标度 = 1、2、4和将(N1,N2)应用于标度
= 1、2、4和将(N1,N2)应用于标度 = 1,2的色度时,需要决策树。
= 1,2的色度时,需要决策树。
图10显示了多尺度处理非常有效。使用比例为 = 1、2、4的运算符的组合始终可以显着改善Chernoff。对于Sowerby数据集,这种增长特别强劲。多尺度能够更好地区分纹理边缘(应打折)和与边界相对应的边缘。它还能够检测不同宽度的边缘(在Sowerby中出现,但在南佛罗里达州很少出现)。
= 1、2、4的运算符的组合始终可以显着改善Chernoff。对于Sowerby数据集,这种增长特别强劲。多尺度能够更好地区分纹理边缘(应打折)和与边界相对应的边缘。它还能够检测不同宽度的边缘(在Sowerby中出现,但在南佛罗里达州很少出现)。
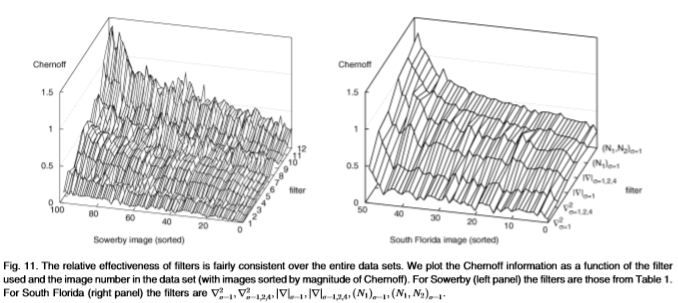
图11:过滤器的相对有效性在整个数据集中相当一致。 我们将Chernoff信息绘制为所使用的过滤器和数据集中的图像编号(图像按Chernoff大小排序)的函数。 对于Sowerby(左面板),过滤器是表1中的过滤器。对于South Florida(右面板),过滤器是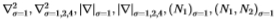 。
。
我们通过学习每个图像的分布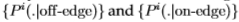 并计算切尔诺夫(Chernoffs),来分析每个图像这些结果的一致性。我们将其绘制为浮雕图,请参见图11。这表明,尽管切尔诺夫信息随图像的不同而变化,但滤镜的相对效率大致相同(我们对图像进行排序,以使切尔诺夫单调增加)。
并计算切尔诺夫(Chernoffs),来分析每个图像这些结果的一致性。我们将其绘制为浮雕图,请参见图11。这表明,尽管切尔诺夫信息随图像的不同而变化,但滤镜的相对效率大致相同(我们对图像进行排序,以使切尔诺夫单调增加)。
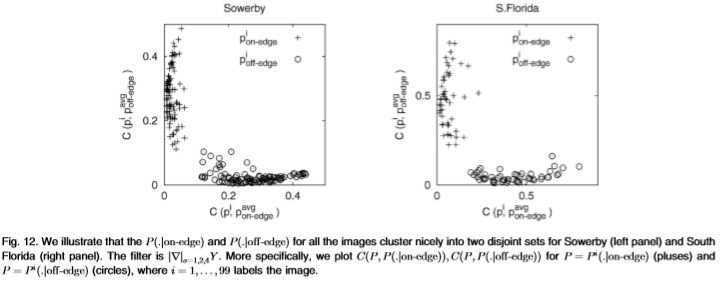
图12:我们说明所有图像的 很好地聚集成了Sowerby(左图)和South Florida(右图)的两个不相交的集合。 过滤器为
很好地聚集成了Sowerby(左图)和South Florida(右图)的两个不相交的集合。 过滤器为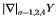 。更具体地说,我们为
。更具体地说,我们为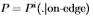 (加号)和
(加号)和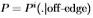 (圆圈)绘制
(圆圈)绘制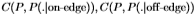 ,其中i = 1,...,99标记图像。
,其中i = 1,...,99标记图像。
图12研究了图像之间分布的一致性。 更准确地说,我们绘制了相对于整个数据集获得的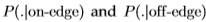 的
的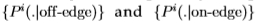 的变化。 变化通过切尔诺夫信息来衡量。 这表明
的变化。 变化通过切尔诺夫信息来衡量。 这表明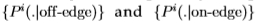 很好地分成了两个不重叠的集合。 因此,图像之间的分布相当一致。
很好地分成了两个不重叠的集合。 因此,图像之间的分布相当一致。
尽管英格兰的乡村道路场景(Sowerby数据集)与佛罗里达州的室内图像(南佛罗里达的数据集)之间存在差异,但最引人注目的观察结果是,不同滤镜的相对有效性大致保持不变,见图11。
3.2.2 面向滤波器组的结果
在学习过滤器组的统计信息时,过度学习是一个重要的问题,因此我们经常使用决策树表示。
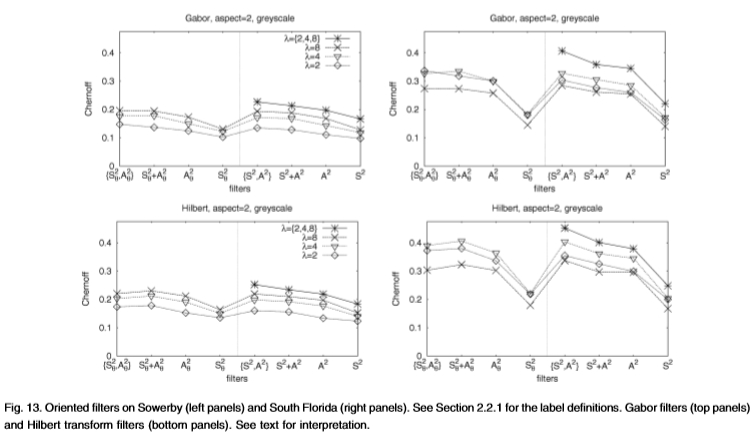
图13:Sowerby(左图)和South Florida(右图)上的定向过滤器。 有关标签定义,请参见第2.2.1节。 Gabor滤波器(顶部面板)和Hilbert变换滤波器(底部面板)。 参见文字进行解释。
我们获得的滤波器组结果有些令人惊讶,请参见图13。我们表明:
1.能量过滤器S2 + A2非常有效,根据Chernoff信息测得,在所有过滤器上使用联合分布(这是最佳方法)几乎没有优势。
2.希尔伯特变换滤波器产生的性能明显好于Gabor滤波器,这可能是由于它们缺少“振铃”。
3.对来自所有不同方向的能量求和,得到了一个一维滤波器,其性能接近于最优(这使一些作者大为惊讶)。
4.最后,包括一维滤波器(请参阅3)的希尔伯特变换滤波器与以前测试过的最好的滤波器(尼兹伯格)具有可比性,请参见图6中的灰度面板。
这些数字适用于宽高比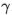 = 2(即,滤波器在频率调谐方向上为其包络的两倍长)。 对于方面
= 2(即,滤波器在频率调谐方向上为其包络的两倍长)。 对于方面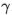 = 1,切尔诺夫信息最多下降10%。 耦合方面
= 1,切尔诺夫信息最多下降10%。 耦合方面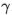 = 1和
= 1和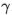 = 2将性能提高了大约5%(超过
= 2将性能提高了大约5%(超过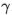 = 2)。
= 2)。
3.3 ROC结果
我们还可以使用ROC曲线评估滤波器,见图5。有两个主要的ROC结果。 首先,请参见第3.3.1节,ROC曲线下的面积与Chernoff信息之间存在简单的经验关系。 而且,根据经验,ROC曲线的大部分形式由其下方的面积确定。 因此,ROC曲线和Chernoff信息给出了非常相似的结果。 其次,请参阅第3.3.2节,我们可以使用ROC曲线将统计边缘检测与南佛罗里达和Sowerby的标准边缘检测器进行比较。
3.3.1与Chernoff信息和ROC区域相关
在本节中,我们提供一个公式,该公式将经验值与我们的滤波器(两个滤波器组)的Chernoff信息和ROC曲线相关联。
首先,在计算用于边缘识别的ROC曲线时,请参见图5的右图,我们注意到它们看起来与具有相同方差的单变量高斯分布的ROC曲线令人惊讶地相似。 这意味着[15],ROC曲线的形式仅取决于数量d'=|u2-u1|/ ,其中u1,u2是高斯的均值,而
,其中u1,u2是高斯的均值,而 2是它们的方差。 ROC曲线下的面积仅取决于相同的d' 且由
2是它们的方差。 ROC曲线下的面积仅取决于相同的d' 且由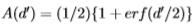 给出。因此,知道ROC曲线下的面积等同于知道ROC曲线。
给出。因此,知道ROC曲线下的面积等同于知道ROC曲线。
自相矛盾的是,ROC曲线大致看起来像具有相同方差的单变量高斯曲线。 经验概率分布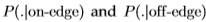 不是遥远的高斯分布。 但是,ROC曲线仅取决于对数似然比
不是遥远的高斯分布。 但是,ROC曲线仅取决于对数似然比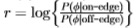 上的感应分布
上的感应分布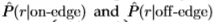 (其中
(其中
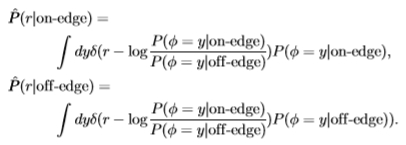
从经验上讲,这些诱导分布通常是近似单变量的高斯分布,至少在两个分布的重叠区域内具有相同的方差,请参见图14。因此,我们预测ROC曲线下的面积与Chernoff信息相关联 边缘和非边缘分布是具有相同方差的单变量高斯分布。 将Chernoff信息计算为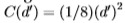 仍然很简单,该信息同样仅取决于d'。
仍然很简单,该信息同样仅取决于d'。
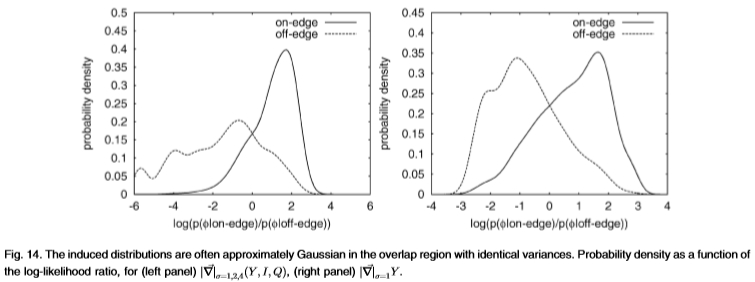
图14:在重叠区域中具有相同方差的感应分布通常近似为高斯分布。 (左图)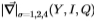 ,(右图)
,(右图)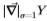 的概率密度与对数似然比的函数。
的概率密度与对数似然比的函数。
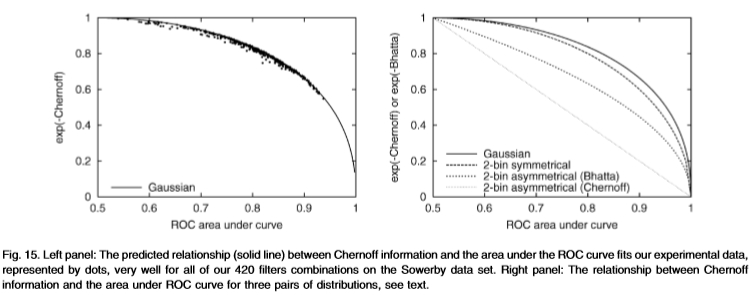
图15:左图:切尔诺夫信息与ROC曲线下面积之间的预测关系(实线)与我们的实验数据吻合,以点表示,非常适合Sowerby数据集上的所有420个滤波器组合。 右面板:三对分布的Chernoff信息与ROC曲线下面积之间的关系,请参见文本。
图15将切尔诺夫信息绘制为ROC曲线下面积的函数。 粗线是假设等高线分布的预测关系。 这些点对应于我们数据集上420个过滤器的经验结果。 所有的点都非常接近预测。 图15的右图绘制了单变量高斯曲线的ROC曲线(实线),2-bin对称分布p =(a,1-a),q =(1-a,a)(虚线)和2- bin不对称p =(1,0),q =(a,1-a)(短划线和虚线的线)。 后者有两条曲线,具体取决于我们将ROC面积与Chernoff信息相关还是与Bhattacharyya系数相关(对于前两个分布,这些数量相等)。
3.3.2 统计和标准边缘检测器的ROC比较
现在,我们将统计边缘检测的性能与Canny边缘检测器的性能进行比较。此外,通过使用Bowyer等人的结果。 [7],[8],我们得到了统计边缘检测与南佛罗里达数据集上其他常规边缘检测器的比较。
将统计边缘检测与常规边缘检测器进行比较存在两个困难。首先,常规边缘检测器通常具有非最大抑制级(Bowyer等人将非最大抑制添加到他们测试的所有边缘检测器中)。其次,大多数传统的边缘检测器包含多个可调参数(对于Canny而言为三个)。这两个困难都可能导致ROC曲线出现偏差,请参见[23]中的示例,并且需要非标准方法来评估边缘检测器响应的真阳性和假阳性。我们将使用Bowyer等人提出的两种评估方法来确定ROC曲线。在这里开发了一种新方法。可以说统计边缘检测的优点是它需要一个参数(阈值),并且可以使用标准ROC和Chernoff标准直接进行评估。
非最大抑制会导致ROC曲线出现两种类型的问题,除非解决这些问题,否则它们会使曲线对地面真实情况的误差极为敏感。首先,非最大抑制可通过防止边缘检测器检测所有地面真实边缘来在真实正值上产生偏差。地面真实边缘位置的小误差可能意味着边缘检测器在边缘的真实位置正确响应,从而抑制了其在地面真实位置的响应。另外,地面真实边缘有时可能是两个像素宽,因此非最大抑制将阻止边缘检测器将两个像素点都标记为边缘。其次,非最大抑制可以大大减少误报的数量。这将发生在ROC曲线中误报率很高的部分(即,当图像中的许多像素被错误地估计为边缘时)。这对应于边缘检测器参数的非常不切实际的选择,因此不能代表具有更实际的参数设置的边缘检测器的行为。
在南佛罗里达州的数据集上,我们调整了方法,以便可以将其直接与Bowyer等人的结果进行比较。首先,我们将非最大抑制应用于统计边缘检测。其次,我们使用Bowyer等人的评估标准(请参阅下一段)来确定真实的阳性和假阳性率。第三,我们使用贝叶斯风险比较了边缘检测器(假设像素同样有可能先验地在边缘上或边缘),因为贝叶斯风险是根据ROC曲线的一部分计算出来的,该ROC曲线对应于边缘检测器参数值的合理选择。
鲍耶(Bowyer)等人确定真假阳性的标准是算法。为了评估真实肯定,构建了一个由地面真实像素组成的列表。第二个列表由检测器标记为边缘的像素组成。该算法通过依次扫描第一列表来进行。如果第一列表中的一个像素在第二列表中的一个元素的三个像素之内,则对正值进行计数并删除第二列表中的元素。这意味着第二个列表中的每个元素最多可以“验证”第一个列表中的一个元素,因此可以防止算法过度计算真实阳性的数量。要评估误报,Bowyeretal。计算边缘检测器在其三值地面真相的区域(b)中标记为边缘的像素数,请参阅第3.1节。这意味着在计算假阳性时,会忽略地面真实边缘的三个像素距离内的边缘检测器响应(就像纹理区域中的边缘检测器响应一样)。这些标准可能会受到批评,请参见示例[23],在这些示例中,它们对边缘检测器的性能提供了误导性的衡量,但通常它们会给出直观上合理的结果。
但是,这些标准仅解决了非最大抑制的第一个问题(例如,对正阳性的偏见)。因此,ROC曲线中仍将存在失真。因此,我们将通过边缘检测器的贝叶斯风险来评估边缘检测器(像素在边缘上和边缘上的优先级相等)。可以从ROC曲线中测量贝叶斯风险,方法是找到曲线上的斜率为45度[15]的点(通常接近假阴性数等于假阳性数的点,并且正好等于如果分布是具有相同方差的单变量高斯分布,则为这一点。
对于Bowyer等人评估的边缘检测器,我们获得的贝叶斯风险的近似值在0.035–0.045的范围内[8]。使用四个等级 = 0、1、2、4(具有非最大抑制和Bowyer等人的评估标准)的梯度滤波器,我们的统计边缘检测得出的贝叶斯风险为0.0350。我们对Canny边缘检测器的实施产生了类似的贝叶斯风险,即0.0352(与Bowyer等人的结果一致并验证了我们的实施)。总体而言,统计边缘检测与[8]中报告的任何边缘检测器一样,均使用相同的评估标准执行。
= 0、1、2、4(具有非最大抑制和Bowyer等人的评估标准)的梯度滤波器,我们的统计边缘检测得出的贝叶斯风险为0.0350。我们对Canny边缘检测器的实施产生了类似的贝叶斯风险,即0.0352(与Bowyer等人的结果一致并验证了我们的实施)。总体而言,统计边缘检测与[8]中报告的任何边缘检测器一样,均使用相同的评估标准执行。
我们在更具挑战性的Sowerby数据集上获得了统计边缘检测与Canny边缘检测器之间的显着差异。在这种情况下,我们没有将非最大抑制应用于统计边缘检测,而是使用了一个附加的分组阶段,如以下部分所述。我们还修改了评估标准,以解决由非最大抑制引起的ROC曲线的两个问题。该标准涉及使用形态学算子来扩大被评估的边缘检测器标记为边缘的像素的数量,并在地面真实边缘周围产生缓冲区(Bowyer等人使用了类似的缓冲区)。它们使非最大抑制所引起的偏差最小化,同时允许地面真相分段中的不精确性。更准确地说,我们在图像上定义了两个二进制字段 ,如果像素x是地面真实边缘,则定义为g(x)=1,如果边缘检测器将像素x标记为边缘,则定义g*(x)=1(否则为g(x)=0和g*(x)=0)。我们将
,如果像素x是地面真实边缘,则定义为g(x)=1,如果边缘检测器将像素x标记为边缘,则定义g*(x)=1(否则为g(x)=0和g*(x)=0)。我们将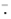 定义为补码(例如
定义为补码(例如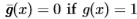 )。我们将n定义为在二进制场上的形态学开口(例如,对于由我们的检测器标记为边缘的点的三像素距离内的任何像素x,g3*(x)=1均为g3*(x)=1)。真假阳性的比例定义为
)。我们将n定义为在二进制场上的形态学开口(例如,对于由我们的检测器标记为边缘的点的三像素距离内的任何像素x,g3*(x)=1均为g3*(x)=1)。真假阳性的比例定义为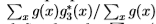 。假假阳性的比例定义为
。假假阳性的比例定义为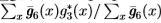 。这些标准也有其局限性,请参见[23]中的讨论,但也会给出合理的结果。我们通过将这些标准应用于统计边缘检测和南佛罗里达数据集上的Canny边缘检测器来测试这些标准,并显示,参见[23],它们给出的结果与使用Boyer等人的标准获得的结果相似(即,两者边缘检测器在南佛罗里达数据集上的表现几乎相同)。
。这些标准也有其局限性,请参见[23]中的讨论,但也会给出合理的结果。我们通过将这些标准应用于统计边缘检测和南佛罗里达数据集上的Canny边缘检测器来测试这些标准,并显示,参见[23],它们给出的结果与使用Boyer等人的标准获得的结果相似(即,两者边缘检测器在南佛罗里达数据集上的表现几乎相同)。

图16:Sowerby的ROC曲线表明统计边缘检测的性能优于Canny。 左:Canny边缘检测器,具有非最大抑制和滞后作用。 中心:未分组的统计边缘检测。 右:分组统计边缘检测(边缘容差= 3)。

图17:顶部面板显示了使用Canny边缘检测器检测到的边缘。 中间面板显示同一图像上统计边缘检测的输出。 底部面板显示了对数似然比,可用来度量边缘强度。 有关图像和基本情况,请参见图7。
使用这些标准,我们的结果表明,在Sowerby数据集上,统计边缘检测器明显优于Canny,请参见图5和6。 16和17。这适用于我们是否将分组用于统计边缘检测,请参见第4节。这并不奇怪,因为Canny检测器仅使用一个标度,而统计边缘检测使用许多标度,它们被最佳地组合(在统计意义上)。 由于所有背景混乱,Sowerby数据集比南佛罗里达州更难分割,因此多尺度处理具有很大的优势,请参见图10。
为了完整性,我们还显示了对数似然比,请参见图17,它可以用作边缘强度的度量[14]。
4 边缘提示的空间分组
大多数标准边缘检测器使用局部空间分组的形式。 例如,Canny边缘检测器[9]使用非最大抑制和滞后作用。 该分组利用图像边缘的先验知识。 边缘通常在空间上是连续的(磁滞)和一个像素宽(非最大抑制)。 迟滞使低对比度边缘能够被检测到,只要它们靠近高对比度边缘。 或者,像Geman和Geman [13]这样的概率模型会施加先验概率,因此,如果在一个像素位置存在边缘,则这会增加在相邻像素处存在边缘的可能性。
现在,我们应用统计边缘检测以包括一种形式的空间分组。 作为学习过程的一部分,自然会产生类似于磁滞和非最大抑制的特性。 这种分组显着改善了边缘检测结果的视觉质量。 但是,自相矛盾的是,它仅对我们的性能标准进行了小幅改进。
我们的分组过程类似于我们学习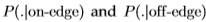 的方法。不同之处在于,我们将滤波器组
的方法。不同之处在于,我们将滤波器组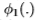 应用于后验分布
应用于后验分布 ,其中
,其中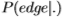 是位置
是位置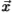 处存在边的后验概率,条件是条件
处存在边的后验概率,条件是条件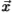 处的滤波器响应
处的滤波器响应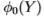 为
为 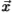 .直觉是,像图17中的对数似然比一样,后验是边缘强度的度量。 (根据数据集测得的像素为边缘的先验概率为0.06)。 我们的分组过程将旧的后验与滤波器组进行卷积,并学习新的“后验”
.直觉是,像图17中的对数似然比一样,后验是边缘强度的度量。 (根据数据集测得的像素为边缘的先验概率为0.06)。 我们的分组过程将旧的后验与滤波器组进行卷积,并学习新的“后验” 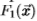 (使用地面事实),然后重复该过程。
(使用地面事实),然后重复该过程。
从理论上讲,完整过程是:1)从真正的后验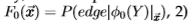 学习开始
学习开始

和3)迭代学习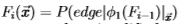 ,因为i = 1、2、3 ... 但是,实际上,我们使用了一个简化的过程,它通过将
,因为i = 1、2、3 ... 但是,实际上,我们使用了一个简化的过程,它通过将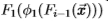 设置为i = 1、2、3 ...来代替第三阶段。
设置为i = 1、2、3 ...来代替第三阶段。
在我们的实验中,我们使用了过滤器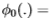
 ,其中I 是身份过滤器。 用于分组(即,对于
,其中I 是身份过滤器。 用于分组(即,对于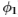 )最有用的过滤器是那些增强后部脊的过滤器(这些脊对应于图像中的边缘)。 这些是高斯的拉普拉斯算子,并附加了渐变滤波器。 当然,身份过滤器很有用(因为它给出了后验)。
)最有用的过滤器是那些增强后部脊的过滤器(这些脊对应于图像中的边缘)。 这些是高斯的拉普拉斯算子,并附加了渐变滤波器。 当然,身份过滤器很有用(因为它给出了后验)。

图18:分组示例 顶行:不分组的后验:F0(x)。 最下一行:分组F1(x)之后的后部。 见文字。
我们在图18中给出了分组的示例。总的来说,我们的方法擅长于滞后并增强不同纹理之间的边缘(即,将边缘提高到阈值以上,因为它们沿着山脊并相互支撑)。纹理的边缘被抑制,因为强和弱边缘倾向于抑制附近的弱平行边缘。我们的方法在三点和拐角处也表现良好,而Canny滤镜经常表现不佳。另一方面,我们似乎并没有像对Canny边缘检测器那样对边缘进行细化以及非最大抑制。这可能是由于我们的方法中使用的量化可能导致相邻像素具有相同的边缘强度(非最大抑制无法解决此问题)。
为了通过分组来量化增益,我们计算切尔诺夫信息。得出的值为0.263(不分组),0.290(一个分组级别),0.282(两个分组级别)和0.274(三个分组级别)。一个分组级别的改进很小(大约百分之十),但是从视觉上看,有一定的改进,见图18。切尔诺夫(Chernoff)在两个和三个级别的分组中的减少可能是由于我们简化的过程引起的。
5 数据集之间的适应
在本节中,我们展示了我们可以学习一个数据集上的条件分布,并使它们适应另一种数据集,而性能却略有下降,而无需了解第二个数据集的基本事实。 这表明我们的结果可以在各个领域之间进行调整。 这也说明我们的结果对地面实况并非过于敏感,因为否则这种适应会导致更大的退化(特别是考虑到Sowerby和South Florida地面实境之间的差异)。
我们注意到Canny讨论了适应性[9],并介绍了估算图像中噪声量的方法,以便动态更改其边缘检测器的参数。 但是,这种适应并不常用。 最近,Grzywacz和Balboa [16]描述了一种使用贝叶斯概率理论的方法,用于基于边缘统计信息的生物视觉系统如何在域与域之间调整其接收场。
形式上,我们仅使用南佛罗里达数据集中的边沿统计信息定义规则以估计Sowerby数据集的分布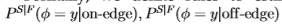 。 同样,我们使用这些规则使用Sowerby的边缘统计数据来估算佛罗里达的分布
。 同样,我们使用这些规则使用Sowerby的边缘统计数据来估算佛罗里达的分布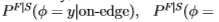
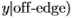 。 (我们使用上标S | F来指示使用南佛罗里达州的分割在Sowerby数据集上估计的分布,反之亦然,对于F | S。)
。 (我们使用上标S | F来指示使用南佛罗里达州的分割在Sowerby数据集上估计的分布,反之亦然,对于F | S。)
我们的适应方法基于使用不同的策略来估计关闭统计
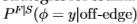 和关闭边缘统计
和关闭边缘统计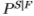
 。
。
偏离统计的策略是利用图像中大多数像素都不是边缘的事实。 因此,对于每个域,我们计算所有像素的滤波器响应的概率分布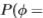 y|all)(这不需要我们知道分割)即可得出
y|all)(这不需要我们知道分割)即可得出 的估算值(更正式地说,我们可以表示
的估算值(更正式地说,我们可以表示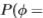 y|all)=
y|all)=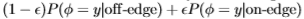 ,其中
,其中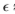
 0.06是图像中边缘的比例。我们的策略设置
0.06是图像中边缘的比例。我们的策略设置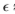 = 0.0,并且通过计算Chernoff信息,我们验证了几乎没有信息丢失。)
= 0.0,并且通过计算Chernoff信息,我们验证了几乎没有信息丢失。)
为了适应数据集之间的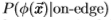 ,我们注意到,对于大多数边际滤波器
,我们注意到,对于大多数边际滤波器 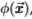 ,分布
,分布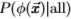 近似于边缘分布
近似于边缘分布
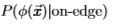
在大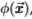 处,请参见图19的左面板和中面板。因此,对于大
处,请参见图19的左面板和中面板。因此,对于大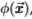 而言,我们无需知道基本事实即可访问
而言,我们无需知道基本事实即可访问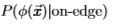 (最大比例因子)。根据经验,我们发现,对于大的
(最大比例因子)。根据经验,我们发现,对于大的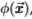 ,指数下降是近似指数的,因此,如果取log
,指数下降是近似指数的,因此,如果取log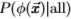 并计算其对大的A的渐近斜率,则它近似于log
并计算其对大的A的渐近斜率,则它近似于log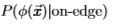 的渐近斜率。此外,如果两个数据集的统计量呈指数下降,则logP
的渐近斜率。此外,如果两个数据集的统计量呈指数下降,则logP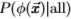 的渐近斜率之比将产生一个恒定的缩放因子k,该因子与两个数据集的
的渐近斜率之比将产生一个恒定的缩放因子k,该因子与两个数据集的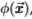 相关。为了适应从南佛罗里达州到Sowerby的变化,我们为梯度滤波器的幅值测量了k = 1.5,请参见图19的右面板。因此,我们采用在Sowerby数据集上测得的分布
相关。为了适应从南佛罗里达州到Sowerby的变化,我们为梯度滤波器的幅值测量了k = 1.5,请参见图19的右面板。因此,我们采用在Sowerby数据集上测得的分布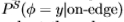 并通过线性比例
并通过线性比例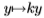 进行调整(其中k是比例因子),以便大y的衰减率类似于南佛罗里达数据集中的
进行调整(其中k是比例因子),以便大y的衰减率类似于南佛罗里达数据集中的 的衰减率。这样就得出了南佛罗里达州边缘统计的估计值
的衰减率。这样就得出了南佛罗里达州边缘统计的估计值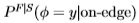 ,见图20。类似地,我们可以根据南佛罗里达州测得的边缘分布来估计Sowerby中的边缘分布。可以证明[23],其他滤波器也有类似的结果,此外,性能对k值不敏感。
,见图20。类似地,我们可以根据南佛罗里达州测得的边缘分布来估计Sowerby中的边缘分布。可以证明[23],其他滤波器也有类似的结果,此外,性能对k值不敏感。

图19:这些图表明,对于Sowerby(左图)和South Florida(中图),logP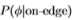 (实线)和logP
(实线)和logP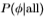 (虚线)的渐近斜率实际上与比例无关。 水平轴标记过滤器的比例,垂直轴是对数概率的渐近斜率。 右图显示Sowerby的logP
(虚线)的渐近斜率实际上与比例无关。 水平轴标记过滤器的比例,垂直轴是对数概率的渐近斜率。 右图显示Sowerby的logP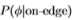 的渐近斜率除以南佛罗里达(实线)和logP
的渐近斜率除以南佛罗里达(实线)和logP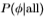 的比率(虚线)均具有(大约)相同的值k = 1.5。
的比率(虚线)均具有(大约)相同的值k = 1.5。
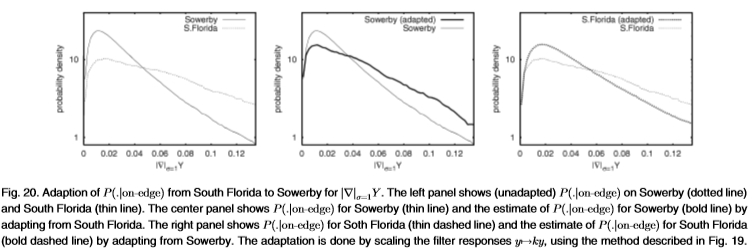
图20: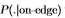 从南佛罗里达州到Sowerby的
从南佛罗里达州到Sowerby的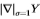 适应性。左图显示(未修改)
适应性。左图显示(未修改)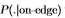 Sowerby(虚线)和South Florida(细线)。 中间面板显示了Sowerby的
Sowerby(虚线)和South Florida(细线)。 中间面板显示了Sowerby的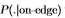 (细线)和Sowerby的
(细线)和Sowerby的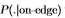 估计(粗线),取自南佛罗里达州。 右面板显示了Soth Florida的
估计(粗线),取自南佛罗里达州。 右面板显示了Soth Florida的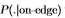 (细虚线)和South Florida的
(细虚线)和South Florida的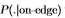 估计值(粗虚线)(根据Sowerby的调整)。 使用图19中描述的方法通过缩放滤波器响应
估计值(粗虚线)(根据Sowerby的调整)。 使用图19中描述的方法通过缩放滤波器响应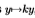 来完成自适应。
来完成自适应。
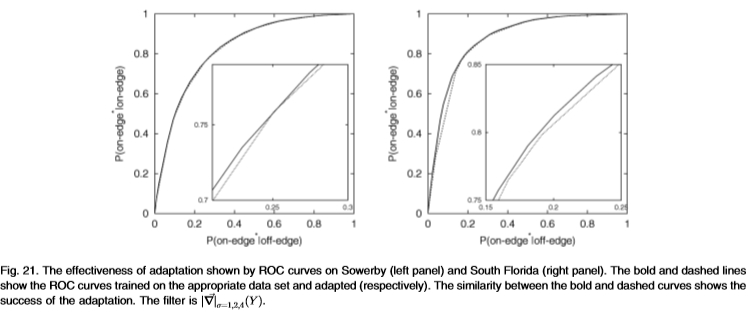
图21:Sowerby(左图)和South Florida(右图)上的ROC曲线显示的适应效果。 粗虚线表示在适当的数据集上训练并分别进行了修改的ROC曲线。 粗曲线和虚线之间的相似性表明了该修改的成功。 过滤器是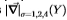 。
。
我们通过调整多尺度滤波器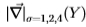 (从Sowerby到South Florida,反之亦然)测试了此过程。 图21显示,尽管数据集的性质非常不同(并且具有不同的基本事实),但适应非常接近。 在Sowerby数据集上,我们获得了真实分布(即使用分布
(从Sowerby到South Florida,反之亦然)测试了此过程。 图21显示,尽管数据集的性质非常不同(并且具有不同的基本事实),但适应非常接近。 在Sowerby数据集上,我们获得了真实分布(即使用分布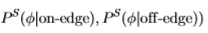 )的ROC面积和Chernoff信息(0.877,0.336)。
)的ROC面积和Chernoff信息(0.877,0.336)。
调整后的分布(即使用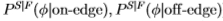 )。 类似地,对于真实的南佛罗里达分布
)。 类似地,对于真实的南佛罗里达分布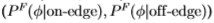 ,我们得到的ROC面积和Chernoff信息为(0.877,0.336),对于经过调整的分布
,我们得到的ROC面积和Chernoff信息为(0.877,0.336),对于经过调整的分布 ,我们得到的(0.867,0.322)。
,我们得到的(0.867,0.322)。
6 讨论与结论
最近有人争论[19],应将感知表达为贝叶斯推理。本文从字面上理解了这一论点,并将其应用于边缘检测的最基本的视觉任务。我们从预先划分的数据集中了解边缘上和边缘外边缘滤波器响应的概率分布,使用对数似然比检验检测边缘,并使用统计量度(切尔诺夫信息和ROC曲线)评估不同的边缘线索。
这种方法使我们能够研究不同边缘提示的有效性以及如何最佳地组合提示(从统计角度来看)。这使我们能够量化多尺度处理的优势以及色度信息的使用。我们使用Sowerby和South Florida这两个截然不同的数据集,并演示了一种将边缘统计信息从一个数据集调整到另一个数据集的方法。
我们将统计边缘检测的结果与标准边缘检测器的结果进行比较。在南佛罗里达州的数据集上,我们的结果与Bowyer等人报告的结果相当。 [7],[8]和Shin等。 [31]用于标准边缘检测器。在Sowerby数据集上,统计边缘检测的性能明显优于Canny边缘检测器[9]。我们注意到Sowerby数据集比South Florida数据集要难得多(我们假设边缘检测器不应对纹理边缘做出反应)。
我们的工作首先作为会议论文发表[20]。 Sidenblath的后续工作将此方法应用于运动跟踪[32]。我们扩展了对区域分割的统计线索的研究[21]。另外,我们将该方法应用于边缘定位任务,并量化了抽取图像时丢失的信息量[22]。
致谢
作者希望感谢美国国家科学基金会(National National Foundation for Foundation)颁发的奖项编号IRI9700446,以及美国国立卫生研究院(NEI)资助的影像科学中心(ARO DAAH049510494)和Smith-Smith授予的资助编号RO1-EY 12691-01。 Kettlewell核心拨款和AFOSR授予ALY F49620-98-1-0197。他们深表感谢使用了英国航空航天公司Sowerby研究中心的Sowerby图像数据集。他们感谢Andy Wright引起我们的注意。他们还感谢K. Bowyer教授允许我们使用南佛罗里达州的数据集。
参考文献
[1] J.J. Atick and A.N. Redlich, “What Does the Retina Know About Natural Scenes?” Neural Computation, vol. 4, pp. 196-210, 1992.
[2] R. Balboa, PhD Thesis. Dept. of Computer Science. Univ. of Alicante, Spain, 1997.
[3] R. Balboa and N.M. Grzywacz, “The Minimal Local-Asperity Hypothesis of Early Retinal Lateral Inhibition,” Neural Computation, vol. 12, pp. 1485-1517, 2000.
[4] R. Balboa and N.M. Grzywacz, “The Distribution of Contrasts and its Relationship with Occlusions in Natural Images,” Vision Research, 2000.
[5] Active Vision. A. Blake and A.L. Yuille, eds., Boston: MIT Press, 1992.
[6] Empirical Evaluation Techniques in Computer Vision. K.W. Bowyer and J. Phillips, eds., IEEE Computer Society Press, 1998.
[7] K. Bowyer, C. Kranenburg, and S. Dougherty, “Edge Detector Evaluation Using Empirical ROC Curves” Proc. Computer Vision and Pattern Recognition, pp. 354-359, 1999.
[8] K.W. Bowyer, C. Kranenburg, and S. Dougherty, “Edge Detector Evaluation Using Empirical ROC Curves,” Computer Vision and Image Understanding, vol. 84, no. 10, pp 77-103, 2001.
[9] J.F. Canny, “A Computational Approach to Edge Detection” IEEE Trans.PatternAnalysisandMachineIntelligence,vol.8,no.6,pp34-43, June 1986.
[10] J. Coughlan, D. Snow, C. English, and A.L. Yuille, “Efficient Optimization of a Deformable Template Using Dynamic Programming” Proc. Computer Vision and Pattern Recognition (CVPR ’98), 1998.
[11] T.M. Cover and J.A. Thomas, Elements of Information Theory. New York: Wiley Interscience Press, 1991.
[12] D.J. Field, “Relations between the Statistics and Natural Images and the Responses Properties of Cortical Cells” J. Optical Soc. Am., vol. A, no. 4, pp. 2379-2394, 1987.
[13] S. Geman and D. Geman, “Stochastic Relaxation, Gibbs Distributions and the Bayesian Restoration of Images” IEEI Trans. Pattern Analysis and Machine Intelligence, vol. 6, pp 721-741, 1984.
[14] D. Geman and B. Jedynak, “An Active Testing Model for Tracking Roads in Satellite Images,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 18, no. 1, pp 1-14, Jan. 1996.
[15] D.M. Green and J.A. Swets, Signal Detection Theory and Psychophysics, second ed. Los Altos, Calif: Peninsula Publishing, 1988.
[16] N.M. Grzywacz and R.M. Balboa, “A Bayesian Theory of Adaptation and Its Application to the Retina,” Neural Computation, vol. 14, pp. 543-559, 2002.
[17] F. Heitger, L. Rosenthaler, R. von der Heydt, E. Peterhans, and D. Kubler, “Simulation of Neural Contour Mechanisms: From Simple to End-Stopped Cells,” Vision Research, vol. 32, pp. 963-981, 1992.
[18] M. Kass, A. Witkin, and D. Terzopoulos, ”Snakes: Active Contour Models,” Proc. First Int’l Conf. Computer Vision, pp. 259-268, 1987.
[19] Perception as Bayesian Inference. D.C. Knill and W. Richards eds., Cambridge Univ. Press, 1996.
[20] S.M. Konishi, A.L. Yuille, J.M. Coughlan, and S.C. Zhu, “Fundamental Bounds on Edge Detection: An Information Theoretic Evaluation of Different Edge Cues,” Proc. Computer Vision and Pattern Recognition (CVPR ’99), 1999.
[21] S. Konishi and A.L. Yuille, “Bayesian Segmentation of Scenes Using Domain Specific Knowledge” Proc. Computer Vision and Pattern Recognition, 2000.
[22] S. Konishi, A.L. Yuille, and J.M. Coughlan, “A Statistical Approach to MultiScale Edge Detection,” Proc. Workshop Generative-Model-Based Vision: GMBV ’02, 2002.
[23] S. Konishi PhD Thesis, Dept. of Biophysics, Univ. of California at Berkeley, 2002.
[24] A.B. Lee, J.G. Huang, and D.B. Mumford, “Random Collage Model for Natural Images” Int’l J. Computer Vision, Oct. 2000.
[25] D. Marr, Vision. San Francisco: W.H. Freeman and Co., 1982.
[26] M. Nitzberg, D. Mumford, and T. Shiota, Filtering, Segmentation and Depth. Springer-Verlag, 1993.
[27] J. Peng and B. Bhanu, “Closed-Loop Object Recognition Using Reinforcement Learning” Pattern Analysis and Machine Intelligence, vol. 20, no. 2, pp 139-154, Feb. 1998.
[28] P. Perona and J. Malik, “Detecting and Localizing Edges Composed of Steps, Peaks, and Roofs” Proc. Third Int’l Conf. Computer Vision, pp. 52-57, 1990. [29] B.D. Ripley, Pattern Recognition and Neural Networks. Cambridge Univ. Press, 1996.
[30] D.L.RudermanandW.Bialek,“StatisticsofNaturalImages:Scaling in the Woods” Physics Review Letter, vol. 73, pp. 814-817, 1994.
[31] M.C. Shin, D. Goldof, and K.W. Bowyer, “Comparison of Edge Detectors Using an Object Recognition Task,” Proc. Computer Vision and Pattern Recognition Conf., pp 360-365, 1999.
[32] H. Sidenblath, “Probabilistic Tracking and Reconstruction of 3D Human Motion in Monocular Video Sequences,” PhD Thesis, Royal Inst. of Technology, Stockholm, 2001.
[33] J. Sullivan, A. Blake, M. Isard, and J. MacCormick, “Object Localization by Bayesian Correlation” Proc. Int’l Conf. Computer Vision, pp. 1068-1075, 1999.
[34] V.N. Vapnik, Statistical Learning Theory. New York: John Wiley and Sons, Inc., 1998.
[35] M.J. Wainwright and E.P. Simoncelli, “Scale Mixtures of Gaussian and the Statistics of Natural Images,” Proc. Neural Information Processing Systems, pp. 855-861, 2000.
[36] A.L. Yuille and J.M. Coughlan, “Fundamental Limits of Bayesian Inference: Order Parameters and Phase Transitions for Road Tracking,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 22. no. 2, Feb. 2000.
[37] A.L. Yuille, J.M. Coughlan, and S.C. Zhu, “A Unified Framework for Performance Analysis of Bayesian Inference,” Proc. The Int’l Soc. for Optical Eng. (SPIE), Apr. 2000.
[38] S.C. Zhu, T.S. Lee, and A.L. Yuille, “Region Competition: Unifying Snakes, Region Growing, and Bayes/MDL for Multiband Image Segmentation,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 18, no. 9, Sept. 1996.
[39] S.C. Zhu and D.B. Mumford, “Prior Learning and Gibbs Reactiondiffusion” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 19, no. 11, Nov. 1997.
[40] S.C. Zhu, Y. Wu, and D. Mumford, “Minimax Entropy Principle and Its Application to Texture Modeling,” Neural Computation, vol. 9. no. 8, Nov. 1997.
有关此主题或任何其他计算主题的更多信息,请访问我们的数字图书馆,网址为: http://computer.org/publications/dlib.
Image Processing and Analysis_8_Edge Detection:Statistical edge detection_ learning and evaluating edge cues——2003的更多相关文章
- Image Processing and Analysis_8_Edge Detection:Edge and line oriented contour detection State of the art ——2011
此主要讨论图像处理与分析.虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来,但鉴于它们与计算机视觉的紧密联系,以 及它们的出处,没有把它们纳入到图像处理与分析中来.同样,这里面也有 ...
- Image Processing and Analysis_8_Edge Detection:Edge Detection Revisited ——2004
此主要讨论图像处理与分析.虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来,但鉴于它们与计算机视觉的紧密联系,以 及它们的出处,没有把它们纳入到图像处理与分析中来.同样,这里面也有 ...
- Image Processing and Analysis_8_Edge Detection: Optimal edge detection in two-dimensional images ——1996
此主要讨论图像处理与分析.虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来,但鉴于它们与计算机视觉的紧密联系,以 及它们的出处,没有把它们纳入到图像处理与分析中来.同样,这里面也有 ...
- Image Processing and Analysis_8_Edge Detection:Multiresolution edge detection techniques ——1995
此主要讨论图像处理与分析.虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来,但鉴于它们与计算机视觉的紧密联系,以 及它们的出处,没有把它们纳入到图像处理与分析中来.同样,这里面也有 ...
- Image Processing and Analysis_8_Edge Detection:Scale-space and edge detection using anisotropic diffusion——1990
此主要讨论图像处理与分析.虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来,但鉴于它们与计算机视觉的紧密联系,以 及它们的出处,没有把它们纳入到图像处理与分析中来.同样,这里面也有 ...
- Image Processing and Analysis_8_Edge Detection:A Computational Approach to Edge Detection——1986
此主要讨论图像处理与分析.虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来,但鉴于它们与计算机视觉的紧密联系,以 及它们的出处,没有把它们纳入到图像处理与分析中来.同样,这里面也有 ...
- Image Processing and Analysis_8_Edge Detection:Theory of Edge Detection ——1980
此主要讨论图像处理与分析.虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来,但鉴于它们与计算机视觉的紧密联系,以 及它们的出处,没有把它们纳入到图像处理与分析中来.同样,这里面也有 ...
- Image Processing and Analysis_8_Edge Detection:Local Scale Control for Edge Detection and Blur Estimation——1998
此主要讨论图像处理与分析.虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来,但鉴于它们与计算机视觉的紧密联系,以 及它们的出处,没有把它们纳入到图像处理与分析中来.同样,这里面也有 ...
- Image Processing and Analysis_8_Edge Detection:Learning to Detect Natural Image Boundaries Using Local Brightness, Color, and Texture Cues ——2004
此主要讨论图像处理与分析.虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来,但鉴于它们与计算机视觉的紧密联系,以 及它们的出处,没有把它们纳入到图像处理与分析中来.同样,这里面也有 ...
随机推荐
- Apache配置优化之开启KeepAlive
在HTTP 1.0中和Apache服务器的一次连接只能发出一次HTTP请求,而KeepAlive参数支持HTTP 1.1版本的一次连接,多次传输功能,这样就可以在一次连接中发出多个HTTP请求.从而避 ...
- python面向对象之类属性,实例属性
python中的属性分为类属性和实例属性,之前已经说过一些,这里主要是对类属性与实例属性的增删改查 首先是对类属性的增删改查,下面这个是对类属性的修改,在书写类时,已经对类属性occupation进行 ...
- PHP爬虫最全总结2-phpQuery,PHPcrawer,snoopy框架中文介绍
第一篇文章介绍了使用原生的PHP和PHP的扩展库实现了爬虫技术.本文尝试使用PHP爬虫框架来写,首先对三种爬虫技术phpQuery,PHPcrawer, snoopy进行对比,然后分析模拟浏览器行为的 ...
- .Net Core 常用开发工具
组件名 描述 可选版本 推荐版本 Visual Studio Community 社区免费版 For Visual Studio 2017 For Visual Studio 2019 Visual ...
- vue警告: component lists rendered with v-for should have explicit keys
warning信息:component lists rendered with v-for should have explicit keys. See https://vuejs.org/guide ...
- 使用kubeadm部署K8S v1.17.0集群
kubeadm部署K8S集群 安装前的准备 集群机器 172.22.34.34 K8S00 172.22.34.35 K8S01 172.22.34.36 K8S02 注意: 本文档中的 etcd . ...
- 最新 中至数据java校招面经 (含整理过的面试题大全)
从6月到10月,经过4个月努力和坚持,自己有幸拿到了网易雷火.京东.去哪儿.中至数据等10家互联网公司的校招Offer,因为某些自身原因最终选择了中至数据.6.7月主要是做系统复习.项目复盘.Leet ...
- AOP实践—ASP.NET MVC5 使用Filter过滤Action参数防止sql注入,让你代码安全简洁
在开发程序的过程中,稍微不注意就会隐含有sql注入的危险.今天我就来说下,ASP.NET mvc 5使用Filter过滤Action参数防止sql注入,让你代码安全简洁.不用每下地方对参数的值都进行检 ...
- javascript判断碰撞检测
javascript判断碰撞检测 点与矩形的碰撞检测 <pre> /** * * @param x1 点 * @param y1 点 * @param x2 矩形view x * @par ...
- 乐字节Java反射之二:实例化对象、接口与父类、修饰符和属性
大家好,小乐继续接着上集:乐字节Java反射之一:反射概念与获取反射源头Class 这次是之二:实例化对象.接口与父类.修饰符和属性 一:实例化对象 之前我们讲解过创建对象的方式,有new .克隆.反 ...
