C++二叉树前中后序遍历（递归&非递归）统一代码格式

统一下二叉树的代码格式，递归和非递归都统一格式，方便记忆管理。

三种递归格式：

前序遍历：

void PreOrder(TreeNode* root, vector<int>&path)
{
    if (root)
    {
        path.emplace_back(root->val);
        PreOrder(root->left, path);
        PreOrder(root->right, path);
    }
}

中序遍历：

void InOrder(TreeNode* root, vector<int>& path)
{
    if (root)
    {
        InOrder(root->left, path);
        path.emplace_back(root->val);
        InOrder(root->right, path);
    }
}

后序遍历：

void PostOrder(TreeNode* root, vector<int>& path)
{
    if (root)
    {
        PostOrder(root->left, path);
        PostOrder(root->right, path);
        path.emplace_back(root->val);
    }
}

三种递归遍历不用多解释。

三种非递归格式：

前序遍历：

void PreOrderCycle(TreeNode* root, vector<int>& path)
{
    stack<pair<TreeNode*, bool>> s;
    s.emplace(make_pair(root, false));
    bool visited;
    while (!s.empty())
    {
        root = s.top().first;
        visited = s.top().second;
        s.pop();
        if (root == NULL)
            continue;
        if (visited)
            path.emplace_back(root->val);
        else
        {
            s.emplace(make_pair(root->right, false));
            s.emplace(make_pair(root->left, false));
            s.emplace(make_pair(root, true));
        }
    }
}

中序遍历：

void InOrderCycle(TreeNode* root, vector<int>& path)
{
    stack<pair<TreeNode*, bool>> s;
    s.emplace(make_pair(root, false));
    bool visited;
    while (!s.empty())
    {
        root = s.top().first;
        visited = s.top().second;
        s.pop();
        if (root == NULL)
            continue;
        if (visited)
            path.emplace_back(root->val);
        else
        {
            s.emplace(make_pair(root->right, false));
            s.emplace(make_pair(root, true));
            s.emplace(make_pair(root->left, false));
        }
    }
}

后序遍历：

void PostOrderCycle(TreeNode* root, vector<int>& path)
{
    stack<pair<TreeNode*, bool>> s;
    s.emplace(make_pair(root, false));
    bool visited;
    while (!s.empty())
    {
        root = s.top().first;
        visited = s.top().second;
        s.pop();
        if (root == NULL)
            continue;
        if (visited)
            path.emplace_back(root->val);
        else
        {
            s.emplace(make_pair(root, true));
            s.emplace(make_pair(root->right, false));
            s.emplace(make_pair(root->left, false));
        }
    }
}

以上三种遍历实现代码行数一模一样，如同递归遍历一样，只有三行核心代码的先后顺序有区别。

解释下三种非递归遍历（以下图举例）：

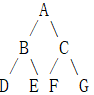
对二叉树而言，将每个框内结点集都看做一个局部，那么局部有   A，A B C，B D E，D，E，C F G，F，G 并且可以发现每个结点元素都是相邻的两个局部的重合结点。

算法流程：

1 每个结点元素都是相邻的两个局部的重合结点。对一个局部排好序后，通过取出一个重合结点过渡到与之相邻的局部进行新的局部排序。
2 用栈来保证局部顺序（排在前面的后入栈，排在后面的先入栈，保证局部元素出栈的顺序一定正确）
3 通过栈顶元素过渡到新局部的排序，对新局部的排序会导致该结点再次入栈，
4 当栈顶出现已完成过渡使命的结点时，就可以彻底出栈输出了，新栈顶元素会继续完成新局部的过渡
5 当所有结点都完成了过渡使命了，就全部出栈了。

参考：

https://www.jianshu.com/p/49c8cfd07410