Codeforces 871C 872E Points, Lines and Ready-made Titles

题

　　OvO http://codeforces.com/contest/871/problem/C

　　( Codeforces Round #440 (Div. 1, based on Technocup 2018 Elimination Round 2) - C )

解

　　问题可以转化为：这些点可以产生的横线与竖线的出现情况

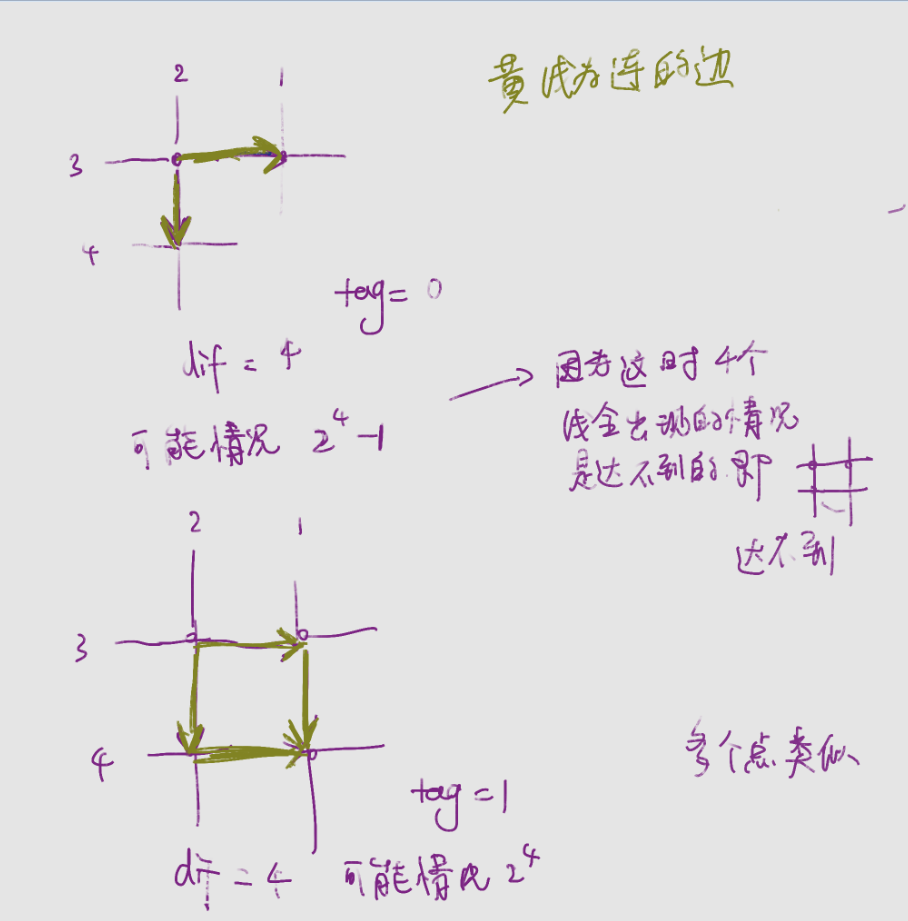
　　首先，对于二维坐标系中的每一行中，对于每个点，如果右边有点，则从该点向右边这个点（相邻的那个点）连一条边（连一条单向的），

　　对于每一列中，对于每个点，如果该点下面有点，则向下边这个点（相邻的那个点）连一条边(同上)

　　（具体实现可以通过排序）

　　然后对于每个点，将与之相连的点并查集合并，合并时如果发现成环，则这个集合tag=1，否则tag=0。

　　算出每个集合中所有点所占据的不重复的行列数，记为dif。

　　对于每个集合，如果这个集合中tag=1，那么这个集合所产生的答案为 2^dif，如果tag=0，那么这个集合所产生的答案为 (2^dif)-1 ，（原因的话，画图可以得出）

　　每个集合的答案是独立的，所以取他们的积

　　

　　

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <set>
#include <map>

using namespace std;

typedef long long ll;

const int N=4e5+44;
const int mod=1e9+7;
const int bas=1e9+44;

struct node{
    int u,v;
    int next;
} edge[2*N];

struct Point
{
	int x,y,id;
} p[N];

int head[N],num,tag[N],cnt[N],dif[N];
int n,ma[N];
set<int> sx[N],sy[N];

int findma(int x)
{
	if(ma[x]==x)
		return x;
	return ma[x]=findma(ma[x]);
}

bool cmp1(Point a,Point b)
{
	if(a.x==b.x)
		return a.y<b.y;
	return a.x<b.x;
}

bool cmp2(Point a,Point b)
{
	if(a.y==b.y)
		return a.x<b.x;
	return a.y<b.y;
}

bool cmp(Point a,Point b)
{
	return a.id<b.id;
}

void addedge(int u,int v)
{
    edge[num].u=u;
    edge[num].v=v;
    edge[num].next=head[u];
    head[u]=num++;
}

void init()
{
	int i,j;
	num=0;
   	memset (head,-1,sizeof(head));
   	for(i=1;i<=n;i++)
   		ma[i]=i,cnt[i]=1;
   	memset(tag,0,sizeof(tag));
   	memset(dif,0,sizeof(dif));
   	for(i=1;i<=n;i++)
   		sx[i].clear(),sy[i].clear();;
}

long long pr(int a, int b)
{
    long long r=1,base=a;
    while(b!=0)
    {
        if(b&1)
            r=(r*base)%mod;
        base=(base*base)%mod;
        b>>=1;
    }
    return r;
}

void solve()
{
	int i,j,a,b,pa,pb;
	ll ans=1,tmp;
	for(i=1;i<=n;i++)
	{
		for(j=head[i];j!=-1;j=edge[j].next)
		{
			a=i; b=edge[j].v;
			pa=findma(a); pb=findma(b);
			if(pa==pb)
			{
				tag[pa]=1;
			}
			else
			{
				ma[pa]=pb;
				tag[pb]=tag[pb]|tag[pa];
				cnt[pb]+=cnt[pa];
			}
		}
	}
	for(i=1;i<=n;i++)
	{
		a=i; pa=findma(a);
		tmp=p[a].x;
		if(sx[pa].find(tmp)==sx[pa].end())
		{
			dif[pa]++;
			sx[pa].insert(tmp);
		}
		tmp=p[a].y;
		if(sy[pa].find(tmp)==sy[pa].end())
		{
			dif[pa]++;
			sy[pa].insert(tmp);
		}
	}
	for(i=1;i<=n;i++)
		if(ma[i]==i)
		{
			tmp=pr(2,dif[i]);
			if(tag[i]==0) tmp--;
			ans=ans*tmp%mod;
		}
	printf("%I64d\n",ans);
}

int main()
{
	int i,j;
	scanf("%d",&n);
	init();
	for(i=1;i<=n;i++)
	{
		scanf("%d%d",&p[i].x,&p[i].y);
		p[i].id=i;
	}
	sort(p+1,p+n+1,cmp1);
	for(i=1;i<n;i++)
		if(p[i].x==p[i+1].x)
			addedge(p[i].id,p[i+1].id);
	sort(p+1,p+n+1,cmp2);
	for(i=1;i<n;i++)
		if(p[i].y==p[i+1].y)
			addedge(p[i].id,p[i+1].id);
	sort(p+1,p+n+1,cmp);
	solve();
	return 0;
}