POJ1222、POJ3279、POJ1753--Flip

POJ1222-EXTENDED LIGHTS OUT

POJ3279-Fliptile

POJ1753-Flip Game

为什么将着三个题放一起讲呢?因为只要搞明白了其中一点，就可以一次3ac了～～

首先讲下每个题目的意思

1.EXTENDED LIGHTS OUT

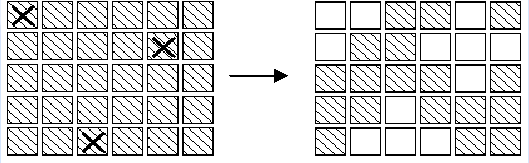
给你5行6列的01矩阵，0代表该点的灯是关闭的，1代表该点的灯是开着的，要求出每一栈灯是否按下，使得所有的灯都熄灭，当然，按下某一盏灯时，它附近的灯也会变成原来相反的状态，如图所示。

---

2.Fliptile

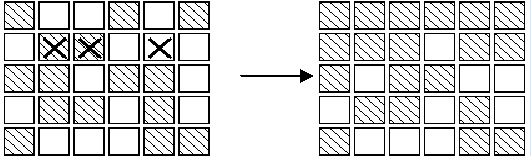
一群奶牛，喜欢白色瓷砖，输入n*m的01矩阵，0表示白色，1表示黑色，问每个砖块该怎么翻转，最后使得所有的颜色都是白色，要求对应的翻转的矩阵对应的字典序最小。每翻转一个，周围的也会变化。如果不可以输出IMPOSSIBLE

---

3.Flip Game

问你针对途中黑白色圈圈，输出将图中所有的颜色全部变成白色或全部变成黑色的最小的一种翻转次数。

如果怎么都翻转失败，输出Impossible

---

通过三个题目意思得知，它们有共同点。最后都要求最后是同一种颜色，而且翻转一个点势必会影响周围的四个的原来的颜色状态

除了第一个，二三都存在Impossible的情况。

下面开始介绍思路(假设求解把所有的点变为0|白色的翻转方案)，对于n*m个格子，每个格子对应有2中状态，那么，我把所有的状态都搜索一遍，找出合适的翻转方案可以不？？当然可以，但是十有八九会T掉。因为光4*4的矩阵就由2^16种状态了，更别说大一点的了。所以暴搜是不可取的。

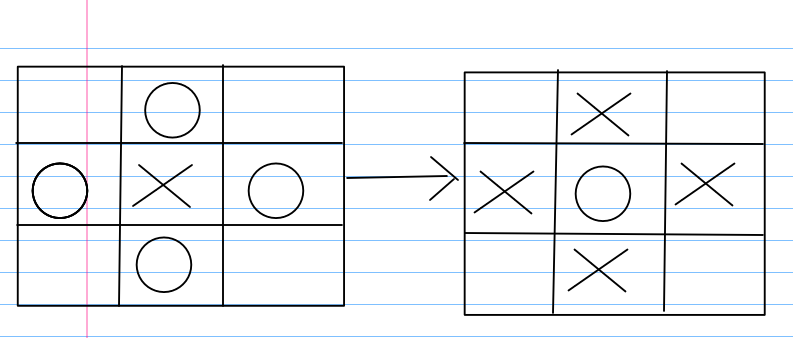
对于每一种操作，都会对应上述这样情况，那我们该从哪个点开始呢？？

因为题目要求矩阵中所有的点都变为同一色，而每个操作互相影响，所以搜索要一行一行来，但是如果后一行的全为0,当前行的某一个操作又影响到上一行和下一行，那后面的又白费了，这样要搞到什么时候？？

试想一下，如果第一行的翻转方案确定了，那么第一行的翻转势必影响到第二行的翻转，第二行的翻转也会影响到第三行的翻转，一直到最后一行。。。也就是说，第一行的翻转方案会影响到整个翻转的结果。

而第一行的翻转状态有多少呢??只有2^m(列号)(用二进制对应每个点的状态)个，这比搜索所有的状态要少多了。

我们还要看一个问题，因为每个点的状态只有两个，0和1，自己翻转肯定改变自己的状态，也会影响周围临近4个点的状态，周围的翻转也会影响自己。但是，有个次数的问题。就如同灯开了2次，4次，6次...到最后还是恢复成原来的状态了。

即如果当前自己为1,自己加周围4个总共翻转了5次，那么自己变成了几？？？5次后，自己变成了0。也就是说，这个点在周围和自己的影响下，变成了目标(0)的状态，那么，这个点还用去翻转吗？？当然不用了

如果是0,一样的道理，所以总结出一点：若cnt表示当前点的状态信息(0|1),sum表示自己加周围临近的4个的所有翻转次数，那么最终这一点是否要翻转取决于(cnt +sum)% 2的值.

当前是1,临近点加自己总共翻转5次，那么自己变成0。即最终自己不需要额外翻转一次
当前是1,临近点加自己总共翻转4次，那么自己变成1,最后自己要多翻转一次才能变成0
当前是0,临近点加自己总共翻转5次，自己变成1,那么自己要多翻转一次才能变成0
当前是0,临近点加自己总共翻转4次，那么自己变成0,不需要额外翻转了

得出结论，当前点是否需要翻转取决于 (原来自己的状态+所有对自己起作用的翻转数）  % 2， 结果为1表明要翻转，为0表明不需要了。这里不清楚的可以自己多写几个看看

好了，第一行的状态数知道了，即每个点的怎么翻转知道了，该怎么求最终结果呢？？

因为已经知道了第一行的所有翻转方案(0 ~ 2^m-1个)，那么对所有方案搜索，直到最后一行的所有的翻转方案都是0就表明第一行的翻转方案是可取的了。。。这什么意思呢

如果搜索到最后，发现最后一行存在几个数是需要翻转的，即这几个数是在上层的翻转作用下变成了1,最后还需要把这几个1翻转一下才会变成0，但是，当你翻转这几个1,势必又影响到上一层，结果上一层又出现几个1。再往上翻，就打乱了所有的状态。所以第一行的翻转方案一定是不可行的。

要点：在第一行的翻转方案搜索中，通过搜索第一行的翻转方案，用第二行的翻转去改变第一行的状态(将1变为0)。接下来的每一行继续用下一行去调整但前行的状态，直至全为0。。。,最后观察最后一行是否需要调整，需要就没戏了，不需要说明OK了。

举个例子，第一行的翻转方案为7：111

上述过程强烈建议手动模拟一下，其实在计算机计算时，先考虑了000的方案，然后会往后找次数更少的方案，看能否找到次数最少的方案(具体看题目要求)。

贴一下代码:

 #include<iostream>
 #include<stdio.h>
 #include<cstring>
 #include<cmath>
 #include<vector>
 #include<stack>
 #include<map>
 #include<set>
 #include<list>
 #include<queue>
 #include<string>
 #include<algorithm>
 #include<iomanip>
 using namespace std;
 const int maxn = ;
 int H[]={,-,,,};
 int V[]={,,,,-};
 int cur[maxn][maxn];//当前结点的颜色
 int res[maxn][maxn];//最终结果
 int flip[maxn][maxn];//是否翻转存放结果
 int n;//行
 int m;//列

 bool IsIn(int x,int y)//判断是否越界
 {
     if(x>= && x<n && y >= && y <m)
         return true;
     return false;
 }

 //查询颜色 0 或 1  | 黑 或 白
 int GetStatus(int x,int y)
 {
     int cnt = cur[x][y];//获取当前的状态
     for(int i =  ;i < ;i++)
     {
         int x2 = x +H[i];
         int y2 = y +V[i];
         if(IsIn(x2,y2))
         {
             cnt += flip[x2][y2];//记录周围的反转次数总和
         }//即周围4个加行自己5个格子的有cnt个反转过
     }
     return cnt % ;//最终确定自己是否需要翻转
 }

 //对第一行的翻转进行搜索
 int SolveRow1()
 {
     for(int i =  ;i < n;i++)//第二行的翻转使第一行为0,第三行的翻转使得第二行为0,依次.
     {
         for(int j = ;j < m;j++)
         {
             if(GetStatus(i-,j))//当前为1，说明要翻转一次  为0 则不需要
             {
                 flip[i][j] = ;//记录翻转一次
             }
         }
     }
     for(int j = ;j< m;j++)//判断最后一行
     {
         if(GetStatus(n-,j))//不是全0 ，即最后一行存在1 要翻转 此时没有翻转的余地了
         {
             return -;//返回-1
         }
     }
     int times = ;//如果最后一行也为0,即所有的都为0了，表明第一行的翻转是可行的
     for(int i = ;i <n;i++)
     {
         for(int j = ;j < m;j++)
         {
             times += flip[i][j];//记录整个矩阵的翻转总次数
         }
     }
     return times;//返回次数
 }

 void Solve()
 {
     int ans = -;
     for(int i = ;i < (<<m);i++)// m列 共  2 ^ m 个选择方案 [0,2^m)
     {
         memset(flip,,sizeof(flip));//初始化操作
         for(int j = ;j < m;j++)
         {
             flip[][m-j-] = i >> j &  ;//1 表示要转换 0表示不动
         }
         int num = SolveRow1();//-1 无解
         if(num >=  && (ans <   || ans > num))
         {
             ans = num;//找出最小翻转次数
             memcpy(res,flip,sizeof(flip));
         }
     }
     if(ans < )
     {
         cout<<"IMPOSSIBLE"<<endl;
     }
     else//打印翻转结果
     {
         for(int i = ;i < n;i++)
         {
             for(int j = ;j < m;j++)
             {
                 cout<<res[i][j];
                 if(j!= m -)
                 {
                     cout<<" ";
                 }
             }
             cout<<endl;
         }
     }
 }

 int main()
 {
     while(cin>>n>>m&& n!= && m!=)
     {
         for(int i = ;i < n;i++)
         {
             for(int j =  ;j < m;j++)
             {
                 cin>>cur[i][j];
             }
         }
         Solve();
     }
     return ;
 }

这里在对这段代码进行简单说明下

  for(int i = ;i < (<<m);i++)// m列 共  2 ^ m 个选择方案 [0,2^m)
     {
         memset(flip,,sizeof(flip));//初始化操作
         for(int j = ;j < m;j++)
         {
             flip[][m-j-] = i >> j &  ;//1 表示要转换 0表示不动
         }
         .. .
         ...
 }

其中i表示从0到2^m次方的所有的翻转方案，就把m看成3把。flip[i][j]表明第i行第j列是否要翻转，所以第一行有2^3==8中翻转方案

---

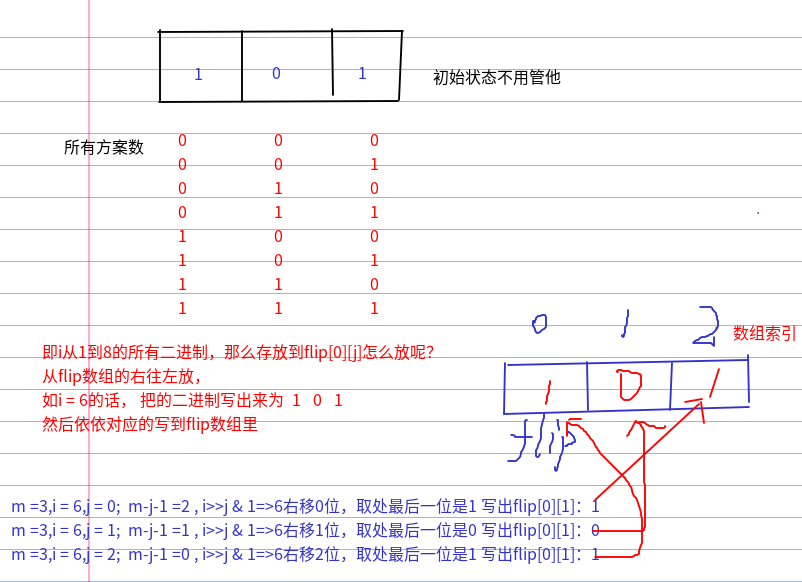
在对解题做个简要说明，POJ1222规模确定，确保可行，直接做即可。POJ3279也十分类似

对于1753,分别需要计算全部翻为白色的最少翻转次数和全部翻为黑色的最少翻转次数。其实只要将输入的b和w对应的1 和 0 调换下，两次始终求解将1 全部换成0的方案数，最终取最小值即可。