EMA指数平滑移动平均

英文参考：http://www.incrediblecharts.com/indicators/exponential_moving_average.php

Exponential moving averages are recommended as the most reliable of the basic moving average types. They provide an element of weighting, with each preceding day given progressively less weighting. Exponential smoothing avoids the problem encountered with simple moving averages, where the average has a tendency to "bark twice": once at the start of the moving average period and again in the opposite direction, at the end of the period. Exponential moving average slope is also easier to determine: the slope is always down when price closes below the moving average and always up when price is above.

Formula

To calculate an exponential moving average (EMA):

• Take today's price multiplied by an EMA%.
• Add this to yesterday's EMA multiplied by (1 - EMA%).

If we recalculate the earlier table we see that the exponential moving average presents a far smoother trend:

Day	1	2	3	4	5	6	7	8	9
Price ($)	16	17	17	10	17	18	17	17	17
33.3% (or 1/3) EMA		16.3	16.5	14.4	15.2	16.2	16.4	16.6	16.8

指数移动平均被认为是最可靠的基本移动平均类型。每个抽样数据都附有以一个权重值，相邻的两个权重值向前递减（也就是前一个权重值比当前权重值减一）。指数移动平均的指数平滑避免了’一般移动平均‘的某些问题，比如一般的移动平均会有“两次跳跃（bark twice）”的现象，从而扭曲数据与实际情况的符合程度。

比如：

Simple Moving Average Formula

To calculate a 5 day simple moving average ("SMA"), take the sum of the last 5 days prices and divide by 5.

Day	1	2	3	4	5	6	7	8	9
Price ($)	16	17	17	10	17	18	17	17	17
5 Day SMA					15.4	15.8	15.8	15.8	17.2

从上面的表格我们可以看到，在第9天，简单移动平均结果是17.2，与第8天的简单移动平均15.8相比有一个较大的跳跃，而第8、9两天的实际数据为17、17并没有变化。在第4天时的数据不仅仅引起当前数值上的下降，而且还对第9天的简单移动平均造成了扭曲，也就是前面说的那个条约。这就是所谓的“bark twice”。也就是说原始数据一次脉冲式跳跃，会导致后面数据的跳跃，并且两次跳跃的方向相反，从而不能很好描述原始数据的变化趋势。因此才有人提出了指数平滑移动平均线Exponential Moving Average，简称EMA。

EXPMA(Exponential Moving Average)译指数平滑移动平均线，简称EMA，

求当日价格X的N日指数平滑移动平均，在股票公式中一般表达为：EMA（X，N），其中X为当日收盘价，N为天数。它真正的公式表达是：当日指数平均值=平滑系数*（当日指数值-昨日指数平均值）+昨日指数平均值；平滑系数=2/（周期单位+1）；由以上公式推导开，得到：EMA(N)=2*X/(N+1)+(N-1)*EMA(N-1)/(N+1)；

可是这个公式的前提是要知道前一天的EMA，如果已知N天的价格，我想求取连续N天的EMA，怎么根据这个N个价格计算EMA呢？根据归纳推算得到公式如下：

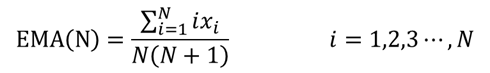
在冈萨雷斯的《数字图像处理》第3版，10.3.7节中，使用移动平均实现对文档图像的阈值处理。在本文中的指数平滑移动平均也可以实现同样的效果，两种方法的差别没有细研究。下面是实现代码，和结果

#include <iostream>
#include<opencv2/opencv.hpp>
using namespace cv;
using namespace std;

void EMA(Mat&src,int N,double b)
{
//    copyMakeBorder(src,src,0,0,N,N,BORDER_REFLECT_101);
    Mat initialRect=src(Rect(,,N,));
    Scalar m0=mean(initialRect);
    double m_last=m0[];
    for(int i=;i<src.rows;i++)
    {
        for(int j=;j<src.cols;j++)
        {
            double X=double(src.at<uchar>(i,j));
            double m_next=*X/(N+)+(N-)*m_last/(N+);
            if(X>m_next*b)
                src.at<uchar>(i,j)=;
            else
                src.at<uchar>(i,j)=;
            m_last=m_next;
        }
    }
}

int main()
{
    Mat src=imread("D:/Qt/MyImage/Fig1049.tif",);
    EMA(src,,0.7);
    imshow("original image",src);
    waitKey();
    return ;
}

下面分别是原图像和经过EMA阈值化后的图像：