透彻网络流-wfx-最大流

前提：

我们想象一下自来水厂到你家的水管网是一个复杂的有向图，每一节水管都有一个最大承载流量。自来水厂不放水，你家就断水了。但是就算自来水厂拼命的往管网里面注水，你家收到的水流量也是上限（毕竟每根水管承载量有限）。你想知道你能够拿到多少水，这就是一种网络流问题。

在网上找了很久资料，虽然讲解网络流的资料很多但是浅显易懂的很少（可能是我太蒻了吧），写这篇文章只希望点进来的人都能学会网络流（都能点赞）

首先

最大流：

何为最大流 简单来说就是水流从一个源点s通过很多路径，经过很多点，到达汇点t，问你最多能有多少水能够到达t点。

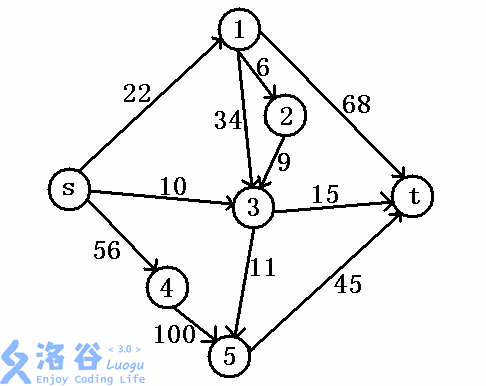
结合图示理解： 从s到t经过若干个点，若干条边，每一条边的水流都不能超过边权值（可以小于等于但不能大于），所以该图的最大流就是10+22+45=77。 如果你还是不能理解，我们就换一种说法，假设s城有inf个人想去t城，但是从s到t要经过一些城市才能到达，（以上图为例）其中s到3城的火车票还剩10张，3到t的火车票还剩15张，其他路以此类推，问最终最多能有多少人能到达t城？

EK:

Edmond—Karp

增广路：

增广路： 增广路是指从s到t的一条路，流过这条路，使得当前的流（可以到达t的人）可以增加。 那么求最大流问题可以转换为不断求解增广路的问题，并且，显然当图中不存在增广路时就达到了最大流。 具体怎么操作呢？ 其实很简单，直接从s到t广搜即可，从s开始不断向外广搜，通过权值大于0的边（因为后面会减边权值，所以可能存在边权为0的边），直到找到t为止，然后找到该路径上边权最小的边，记为mi，然后最大流加mi，然后把该路径上的每一条边的边权减去mi，直到找不到一条增广路（从s到t的一条路径）为止。（为什么要用mi呢？你要争取在这条路上多走更多人，但又不能让人停在某个城市）

代码：

#include<cstdio>
#include<cstdlib>
#include<queue>
#include<iostream>
using namespace std;
const int inf = 2147483647;
const int MAXN = 100100;
int head[MAXN],cnt = 1,low[MAXN],pre[MAXN],n,m,S,T;
int maxflow;
bool v[MAXN];
inline int read(){
	int res = 0; char ch = getchar(); bool bo = false;
	while(ch < '0' || ch > '9') bo = (ch == '-'), ch = getchar();
	while(ch >= '0' && ch <= '9') res = (res << 1) + (res << 3) + (ch ^ 48), ch = getchar();
	return bo ? -res : res;
}
struct node{int nxt,to,dis;}e[MAXN<<1];
void add(int from,int to,int dis)
{
	e[++cnt]= (node){head[from],to,dis};
	head[from]=cnt;
}
void EK()
{
	int x=T;
	while(x!=S)
	{
		int i=pre[x];
		e[i].dis-=low[T];
		e[i^1].dis+=low[T];
		x=e[i^1].to;
	}
	maxflow += low[T];
}
queue <int> q;
bool bfs()
{
	for(int i=1;i<=n;i++)v[i]=0;
	while(q.size()) q.pop();
	v[S]=1;
	q.push(S);
	low[S]=inf;
	while(q.size())
	{
		int x=q.front();
		q.pop();
		for(int i=head[x];i;i=e[i].nxt)
		{
			if(e[i].dis > 0)
			{
				int y=e[i].to;
				if(v[y])continue;
				low[y]=min(low[x],e[i].dis);
				pre[y]=i;
				q.push(y);v[y]=1;
				if(y==T)return true;
			}
		}
	}
	return false;
}
int main()
{
	n=read();m=read();S=read();T=read();
	int x,y,c;
	for(int i=1;i<=m;i++)
	{
		x=read();y=read();c=read();
		add(x,y,c); add(y,x,0);
	}
	while(bfs()) EK();
	printf("%d\n",maxflow);
	return 0;
}

　　

Dinic：

Dinic算法分为两个步骤：

1. bfs分层(在EK中bfs是用于寻找增广路的)
2. dfs增广(dfs？EK中貌似没有这玩意啊，确定能高效？)
3. 咦！刚才不是说两个步骤吗？重复执行1.2.直到图中无增广路为止

什么意思呢？

与EK一样，我们仍要通过bfs来判断图中是否还存在增广路，但是DInic算法里的bfs略有不同，这次，我们不用记录路径，而是给每一个点分层，对于任意点i，从s到i每多走过一个点，就让层数多一。

其实每次只找层数大一的，认为找最短增广路，为神魔呢：

有了分层，我们就不会选s->1->2->4->5->3->t了

刚才说了的，分完层下一步是dfs增广。

在Dinic中，我们找增广路是用深搜：

代码：

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N = 100100;
const int inf = 214748347;
int cnt=1,head[10010],d[10010],n,m,s,t,maxflow;
bool v[N];
struct node{int nxt,to,dis;}e[N<<1];
void add(int from,int to,int dis)
{
	e[++cnt] = (node){head[from],to,dis};
	head[from]=cnt;
}

queue <int> q;
bool bfs()
{
	memset(d,0,sizeof d);
	while(q.size())q.pop();
	q.push(s);
	d[s]=1;
	while(q.size())
	{
		int x=q.front();q.pop();
		for(int i=head[x];i;i=e[i].nxt)
		{
			int y=e[i].to;
			if(e[i].dis && !d[y])
			{
				q.push(y);
				d[y]=d[x]+1;
				if(e[i].to==t)return 1;
			}
		}
	}
	return 0;
}
int dinic(int x,int flow)
{
	if(x==t)return flow;
	int rest=flow,k;
	for(int i=head[x];i&&rest;i=e[i].nxt)
	{
		int y=e[i].to;
		if(e[i].dis&&d[y]==d[x]+1)
		{
			k=dinic(y,min(rest,e[i].dis));
			if(!k) d[y]=0;
			e[i].dis-=k;
			e[i^1].dis+=k;
			rest-=k;
		}
	}
	return flow-rest;
}
int main()
{
	scanf("%d%d%d%d",&n,&m,&s,&t);
	int x,y,c;
	for(int i=1;i<=m;i++)
	{
		scanf("%d%d%d",&x,&y,&c);
		add(x,y,c);add(y,x,0);
	}
	int flow=0;
	while(bfs())
	{
		while(flow=dinic(s,inf)) maxflow+=flow;
	}
	printf("%d\n",maxflow);
	return 0;
}

　　

还有一种超强的优化：当前弧（边）优化：

我们定义一个数组cur记录当前边（弧）（功能类比邻接表中的head数组，只是会随着dfs的进行而修改），

每次我们找过某条边（弧）时，修改cur数组，改成该边（弧）的编号，

那么下次到达该点时，会直接从cur对应的边开始（也就是说从head到cur中间的那一些边（弧）我们就不走了）。

有点抽象啊，感觉并不能加快，然而实际上确实快了很多。

代码：

bool bfs()
{
	for(int i=1;i<=n;i++)
	{
		cur[i]=head[i];///////////////////只修改这几处，让你的代码飞快，相当于节省了dfs
　　　　　　　　　　d[i]=0；///////中的链式前向星，因为head【】的边有的已经在前面使用
	}
	while(q.size())q.pop();
	q.push(s);
	d[s]=1;
	while(q.size())
	{
		int x=q.front();q.pop();
		for(int i=head[x];i;i=e[i].nxt)
		{
			int y=e[i].to;
			if(e[i].dis && !d[y])
			{
				q.push(y);
				d[y]=d[x]+1;
				if(e[i].to==t)return 1;
			}
		}
	}
	return 0;
}
int dinic(int x,int flow)
{
	if(x==t)return flow;
	int rest=flow,k;
	for(int i=cur[x];i&&rest;i=e[i].nxt)//////////////////
	{
		cur[x]=i;/////////////////
		int y=e[i].to;
		if(e[i].dis&&d[y]==d[x]+1)
		{
			k=dinic(y,min(rest,e[i].dis));
			if(!k) d[y]=0;
			e[i].dis-=k;
			e[i^1].dis+=k;
			rest-=k;
		}
	}
	return flow-rest;
}

　　

感谢__wfx 一下午的讲解，自己明白了很多

！！！！！！！！！！！！！！！！！！

缘来是你