从编辑距离、BK树到文本纠错

搜索引擎里有一个很重要的话题，就是文本纠错，主要有两种做法，一是从词典纠错，一是分析用户搜索日志，今天我们探讨使用基于词典的方式纠错，核心思想就是基于编辑距离，使用BK树。下面我们来逐一探讨：

编辑距离

1965年，俄国科学家Vladimir

Levenshtein给字符串相似度做出了一个明确的定义叫做Levenshtein距离，我们通常叫它“编辑距离”。

字符串A到B的编辑距离是指，只用插入、删除和替换三种操作，最少需要多少步可以把A变成B。例如，从FAME到GATE需要两步（两次替换），从GAME到ACM则需要三步（删除G和E再添加C）。Levenshtein给出了编辑距离的一般求法，就是大家都非常熟悉的经典动态规划问题。

 class LevenshteinDistanceFunction {

        private final boolean isCaseSensitive;

        public LevenshteinDistanceFunction(boolean isCaseSensitive) {
            this.isCaseSensitive = isCaseSensitive;
        }

        public int distance(CharSequence left, CharSequence right) {
            int leftLength = left.length(), rightLength = right.length();

            // special cases.
            if (leftLength == 0)
                return rightLength;
            if (rightLength == 0)
                return leftLength;

            // Use the iterative matrix method.
            int[] currentRow = new int[rightLength + 1];
            int[] nextRow    = new int[rightLength + 1];

            // Fill first row with all edit counts.
            for (int i = 0; i <= rightLength; i++)
                currentRow[i] = i;

            for (int i = 1; i <= leftLength; i++) {
                nextRow[0] = i;

                for(int j = 1; j <= rightLength; j++) {
                    int subDistance = currentRow[j - 1]; // Distance without insertions or deletions.
                    if (!charEquals(left.charAt(i - 1), right.charAt(j - 1), isCaseSensitive))
                            subDistance++; // Add one edit if letters are different.
                    nextRow[j] = Math.min(Math.min(nextRow[j - 1], currentRow[j]) + 1, subDistance);
                }

                // Swap rows, use last row for next row.
                int[] t = currentRow;
                currentRow = nextRow;
                nextRow = t;
            }

            return currentRow[rightLength];
        }

    }

BK树

编辑距离的经典应用就是用于拼写检错，如果用户输入的词语不在词典中，自动从词典中找出编辑距离小于某个数n的单词，让用户选择正确的那一个，n通常取到2或者3。

这个问题的难点在于，怎样才能快速在字典里找出最相近的单词？可以像 使用贝叶斯做英文拼写检查（c#) 里是那样，通过单词自动修改一个单词，检查是否在词典里，这样有暴力破解的嫌疑，是否有更优雅的方案呢？

1973年，Burkhard和Keller提出的BK树有效地解决了这个问题。BK树的核心思想是：

令d(x,y)表示字符串x到y的Levenshtein距离，那么显然：
d(x,y) = 0 当且仅当 x=y （Levenshtein距离为0 <==> 字符串相等）
d(x,y) = d(y,x) （从x变到y的最少步数就是从y变到x的最少步数）
d(x,y) + d(y,z) >= d(x,z) （从x变到z所需的步数不会超过x先变成y再变成z的步数）

最后这一个性质叫做三角形不等式。就好像一个三角形一样，两边之和必然大于第三边。

BK建树

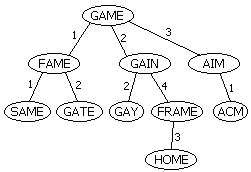
首先我们随便找一个单词作为根（比如GAME）。以后插入一个单词时首先计算单词与根的Levenshtein距离：如果这个距离值是该节点处头一次出现，建立一个新的儿子节点；否则沿着对应的边递归下去。例如，我们插入单词FAME，它与GAME的距离为1，于是新建一个儿子，连一条标号为1的边；下一次插入GAIN，算得它与GAME的距离为2，于是放在编号为2的边下。再下次我们插入GATE，它与GAME距离为1，于是沿着那条编号为1的边下去，递归地插入到FAME所在子树；GATE与FAME的距离为2，于是把GATE放在FAME节点下，边的编号为2。

BK查询

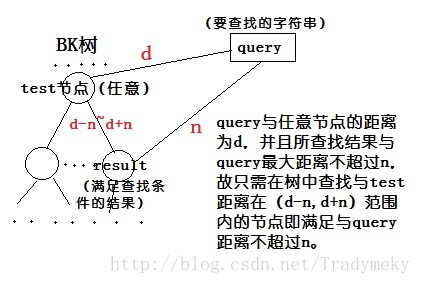
如果我们需要返回与错误单词距离不超过n的单词，这个错误单词与树根所对应的单词距离为d，那么接下来我们只需要递归地考虑编号在d-n到d+n范围内的边所连接的子树。由于n通常很小，因此每次与某个节点进行比较时都可以排除很多子树。

可以通过下图（来自 超酷算法（1）：BK树 （及个人理解））理解：

BK 实现

知道了原理实现就简单了，这里从github找一段代码

建树：

public boolean add(T t) {
        if (t == null)
            throw new NullPointerException();

        if (rootNode == null) {
            rootNode = new Node<>(t);
            length = 1;
            modCount++; // Modified tree by adding root.
            return true;
        }

        Node<T> parentNode = rootNode;
        Integer distance;
        while ((distance = distanceFunction.distance(parentNode.item, t)) != 0
                || !t.equals(parentNode.item)) {
            Node<T> childNode = parentNode.children.get(distance);
            if (childNode == null) {
                parentNode.children.put(distance, new Node<>(t));
                length++;
                modCount++; // Modified tree by adding a child.
                return true;
            }
            parentNode = childNode;
        }

        return false;
    }

查找：

 public List<SearchResult<T>> search(T t, int radius) {
        if (t == null)
            return Collections.emptyList();
        ArrayList<SearchResult<T>> searchResults = new ArrayList<>();
        ArrayDeque<Node<T>> nextNodes = new ArrayDeque<>();
        if (rootNode != null)
            nextNodes.add(rootNode);

        while(!nextNodes.isEmpty()) {
            Node<T> nextNode = nextNodes.poll();
            int distance = distanceFunction.distance(nextNode.item, t);
            if (distance <= radius)
                searchResults.add(new SearchResult<>(distance, nextNode.item));
            int lowBound = Math.max(0, distance - radius), highBound = distance + radius;
            for (Integer i = lowBound; i <= highBound; i++) {
                if (nextNode.children.containsKey(i))
                    nextNodes.add(nextNode.children.get(i));
            }
        }

        searchResults.trimToSize();
        Collections.sort(searchResults);
        return Collections.unmodifiableList(searchResults);
    }

使用BK树做文本纠错

准备词典，18万的影视名称：

测试代码：

  static void outputSearchResult( List<SearchResult<CharSequence>> results){
        for(SearchResult<CharSequence> item : results){
            System.out.println(item.item);
        }
    }

    static void test(BKTree<CharSequence> tree,String word){
        System.out.println(word+"的最相近结果：");
        outputSearchResult(tree.search(word,Math.max(1,word.length()/4)));
    }

    public static void main(String[] args) {

        BKTree<CharSequence> tree = new BKTree(DistanceFunctions.levenshteinDistance());
        List<String> testStrings = FileUtil.readLine("./src/main/resources/act/name.txt");
        System.out.println("词典条数："+testStrings.size());
        long startTime = System.currentTimeMillis();
        for(String testStr: testStrings){
            tree.add(testStr.replace(".",""));
        }
        System.out.println("建树耗时："+(System.currentTimeMillis()-startTime)+"ms");
        startTime = System.currentTimeMillis();
        String[] testWords = new String[]{
                "湄公河凶案",
                "葫芦丝兄弟",
                "少林足球"
        };

        for (String testWord: testWords){
            test(tree,testWord);
        }
        System.out.println("测试耗时："+(System.currentTimeMillis()-startTime)+"ms");
    }

结果：

词典条数：18513
建树耗时：421ms
湄公河凶案的最相近结果：
湄公河大案
葫芦丝兄弟的最相近结果：
葫芦兄弟
少林足球的最相近结果：
少林足球
笑林足球
测试耗时：20ms

参考：

http://blog.csdn.net/tradymeky/article/details/40581547

https://github.com/sk-scd91/BKTree

https://www.cnblogs.com/data2value/p/5707973.html

---

作者：Jadepeng

出处：jqpeng的技术记事本--http://www.cnblogs.com/xiaoqi

您的支持是对博主最大的鼓励，感谢您的认真阅读。

本文版权归作者所有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。