【NOIP2015提高组】 Day1 T3 斗地主
【题目描述】
牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共54张牌来进行的扑克牌游戏。在斗地主中，牌的大小关系根据牌的数码表示如下：3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王，而花色并不对牌的大小产生影响。每一局游戏中，一副手牌由n张牌组成。游戏者每次可以根据规定的牌型进行出牌，首先打光自己的手牌一方取得游戏的胜利。
现在，牛牛只想知道，对于自己的若干组手牌，分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。
需要注意的是，本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。
具体规则如下：
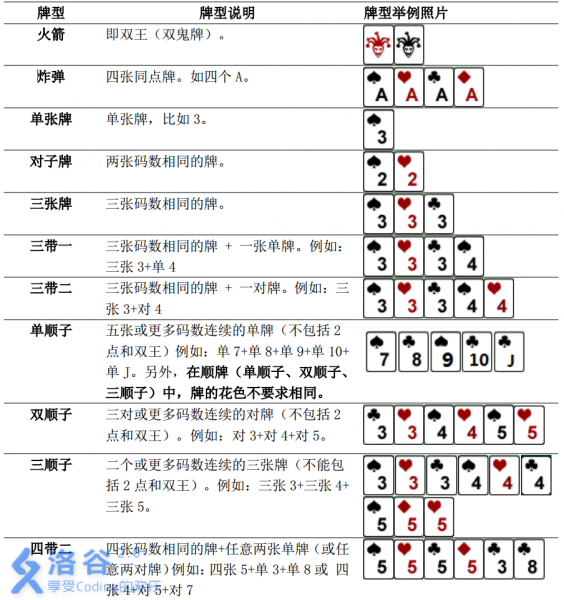
本题数据随机，不支持hack，要hack或强力数据请点击这里
输入输出格式
输入格式：
第一行包含用空格隔开的2个正整数T和n，表示手牌的组数以及每组手牌的张数。
接下来T组数据，每组数据n行，每行一个非负整数对aibi表示一张牌，其中ai示牌的数码，bi表示牌的花色，中间用空格隔开。特别的，我们用1来表示数码A，11表示数码J，12表示数码Q，13表示数码K；黑桃、红心、梅花、方片分别用1-4来表示；小王的表示方法为01，大王的表示方法为02。
输出格式：
共T行，每行一个整数，表示打光第i手牌的最少次数。
输入输出样例
1 8
7 4
8 4
9 1
10 4
11 1
5 1
1 4
1 1
3
1 17
12 3
4 3
2 3
5 4
10 2
3 3
12 2
0 1
1 3
10 1
6 2
12 1
11 3
5 2
12 4
2 2
7 2
6
说明
样例1说明
共有1组手牌，包含8张牌：方片7，方片8，黑桃9，方片10，黑桃J，黑桃5，方片A以及黑桃A。可以通过打单顺子（方片7，方片8，黑桃9，方片10，黑桃J），单张牌（黑桃5）以及对子牌（黑桃A以及方片A）在3次内打光。
对于不同的测试点， 我们约定手牌组数T与张数n的规模如下：
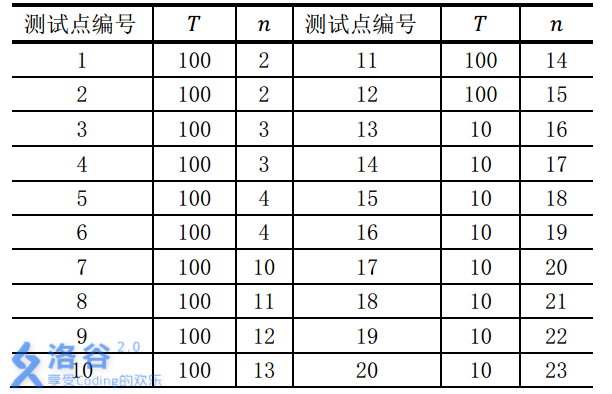
数据保证：所有的手牌都是随机生成的。
自测时果断打了个状压dp，其中f[i]表示当前手上牌的状态为i时需要的最少出牌次数（i的第k个二进制位表示排序后的第k张牌是否出手）。f[i]的转移比较复杂，因此代码打了200+行.....
时间复杂度为O(4*3^7)，但由于f[i]转移条件判断较为耗时，转移方法较多，常数巨大！！
结果这个状压代码只拿了80分...最后四个点TLE（如果不是多组数据就A了.....）
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#define M 18
#define N 14
#define INF 123123123
using namespace std;
int n,st,f[<<]={},cnt[M]={},a[M]={},l[M]={},r[M]={}; bool hf(int x){
bool wei1,wei2;
for(int i=;i<n;i++){
wei1=x&(<<i); wei2=x&(<<(i-));
if(a[i]==a[i-]&&wei2&&(!wei1)) return ;
}
return ;
}
int dan(int y,int x){
if(l[x]==-) return st;
int k=(<<(r[x]-l[x]+))-;
int delta=(y>>l[x])&k;
if(delta){
delta=(delta<<)&k;
y=(y&((<<l[x])-))|(delta<<l[x])|((y>>(r[x]+))<<(r[x]+));
return y;
}
return st;
}
int dui(int y,int x){
if(l[x]==-) return st;
int k=(<<(r[x]-l[x]+))-;
int delta=(y>>l[x])&k;
if((delta<<)&k){
delta=(delta<<)&k;
y=(y&((<<l[x])-))|(delta<<l[x])|((y>>(r[x]+))<<(r[x]+));
return y;
}
return st;
}
int san(int y,int x){
if(l[x]==-) return st;
int k=(<<(r[x]-l[x]+))-;
int delta=(y>>l[x])&k;
if((delta<<)&k){
delta=(delta<<)&k;
y=(y&((<<l[x])-))|(delta<<l[x])|((y>>(r[x]+))<<(r[x]+));
return y;
}
return st;
}
int zha(int y,int x){
if(l[x]==-) return st;
int k=(<<(r[x]-l[x]+))-;
int delta=(y>>l[x])&k;
if((delta<<)&k){
delta=(delta<<)&k;
y=(y&((<<l[x])-))|(delta<<l[x])|((y>>(r[x]+))<<(r[x]+));
return y;
}
return st;
}
int sandaiyi(int y,int x,int dai){
y=san(y,x);
if(y==st) return st;
return dan(y,dai);
}
int sandaier(int y,int x,int dai){
y=san(y,x);
if(y==st) return st;
return dui(y,dai);
}
int sidaier(int y,int x,int dai1,int dai2){
y=zha(y,x);
if(y==st) return st;
y=dan(y,dai1);
if(y==st) return st;
return dan(y,dai2);
}
int sidaidui(int y,int x,int dai1,int dai2){
y=zha(y,x);
if(y==st) return st;
y=dui(y,dai1);
if(y==st) return st;
return dui(y,dai2);
}
int shunzi(int y,int ll,int rr){
for(int i=ll;i<=rr;i++){
y=dan(y,i);
if(y==st) return st;
}
return y;
}
int liandui(int y,int ll,int rr){
for(int i=ll;i<=rr;i++){
y=dui(y,i);
if(y==st) return st;
}
return y;
}
int sanshun(int y,int ll,int rr){
for(int i=ll;i<=rr;i++){
y=san(y,i);
if(y==st) return st;
}
return y;
}
int Main(){
memset(cnt,,sizeof(cnt));
memset(a,,sizeof(a));
memset(l,-,sizeof(l)); memset(r,-,sizeof(r));
for(int i=;i<=n;i++){
int x,k; scanf("%d%d",&x,&k);
if(x<){
if(x==) x=;
else if(x==) x=;
else x=;
}
x=+(x-+N)%N;
cnt[x]++;
}
for(int i=,j=;i<=N;i++){
bool ck=;
while(cnt[i]){
cnt[i]--;
if(ck){l[i]=j; ck=;}
a[j++]=i;
}
if(!ck) r[i]=j-;
}
st=(<<n)-;
for(int i=st;i>=;i--) f[i]=INF;
f[st]=;
for(int i=st;i;i--) if(hf(i)){
if(i==){
f[st]=;
}
for(int j=;j<=N;j++){
int y=dan(i,j);
if(y!=st) f[y]=min(f[y],f[i]+);
}
for(int j=;j<=N;j++){
int y=dui(i,j);
if(y!=st) f[y]=min(f[y],f[i]+);
}
for(int j=;j<=N;j++){
int y=san(i,j);
if(y!=st) f[y]=min(f[y],f[i]+);
}
for(int j=;j<N;j++){
int y=zha(i,j);
if(y!=st) f[y]=min(f[y],f[i]+);
}
for(int j=;j<=N;j++) if(l[j]!=-&&(r[j]-l[j]>)){
for(int k=;k<=N;k++) if(l[k]!=-){
int y=sandaiyi(i,j,k);
if(y!=st) f[y]=min(f[y],f[i]+);
}
}
for(int j=;j<=N;j++) if(l[j]!=-&&(r[j]-l[j]>)){
for(int k=;k<=N;k++) if(l[k]!=-){
int y=sandaier(i,j,k);
if(y!=st) f[y]=min(f[y],f[i]+);
}
}
for(int j=;j<N;j++) if(l[j]!=-){
for(int k=j+;k<=N-;k++) if(l[k]!=-){
int y=shunzi(i,j,k);
if(y!=st) f[y]=min(f[y],f[i]+);
}
}
for(int j=;j<N;j++) if(l[j]!=-&&(r[j]-l[j]>)){
for(int k=j+;k<=N-;k++) if(l[k]!=-&&(r[k]-l[k]>)){
int y=liandui(i,j,k);
if(y!=st) f[y]=min(f[y],f[i]+);
}
}
for(int j=;j<N;j++) if(l[j]!=-&&(r[j]-l[j]>)){
for(int k=j+;k<=N-;k++) if(l[k]!=-&&(r[k]-l[k]>)){
int y=sanshun(y,j,k);
if(y!=st) f[y]=min(f[y],f[i]+);
}
}
for(int j=;j<=N;j++) if(l[j]!=-&&(r[j]-l[j]>)){
for(int k=;k<=N;k++) if(l[k]!=-){
for(int L=;L<=N;L++) if(l[L]!=-){
int y=sidaier(i,j,k,L);
if(y!=st) f[y]=min(f[y],f[i]+);
}
}
}
for(int j=;j<=N;j++) if(l[j]!=-&&(r[j]-l[j]>)){
for(int k=;k<=N;k++) if(l[k]!=-){
for(int L=;L<=N;L++) if(l[L]!=-){
int y=sidaidui(i,j,k,L);
if(y!=st) f[y]=min(f[y],f[i]+);
}
}
}
}
printf("%d\n",f[]);
} int main(){
freopen("landlords.in","r",stdin);
freopen("landlords.out","w",stdout);
int cas; scanf("%d%d",&cas,&n);
while(cas--) Main();
}
事实证明我想多了...
直接上爆搜，暴力枚举单顺，双顺和三顺，剩下的牌直接贪心（即按四带二，四带一对，四代两对，三带一，三代二，炸弹，三条，对子，单牌的顺序出，不难看出这么出牌是最优的,即出牌次数取决于顺的选择方式）。
时间复杂度O(玄学) ，所有点本地0.01s内跑出
代码：
#include<iostream>
#include<cstdio>
#include<cstring>
#define M 100
#define N 14
using namespace std;
int n,ans=;
int a[M]={},c[M]={}; int get(){
c[]=c[]=c[]=c[]=c[]=;
for(int i=;i<=N;i++) c[a[i]]++;
int sum=;
while(c[]&&c[]>=) c[]--,c[]-=,sum++;
while(c[]&&c[]>=) c[]--,c[]-=,sum++;
while(c[]&&c[]) c[]--,c[]--,sum++;
while(c[]&&c[]) c[]--,c[]--,sum++;
while(c[]&&c[]) c[]--,c[]--,sum++;
return sum+c[]+c[]+c[]+c[];
} void dfs(int x){
if(x>=ans) return;
ans=min(ans,x+get());
for(int i=;i<=;i++){
if(a[i]==||a[i+]==||a[i+]==||a[i+]==) continue;
for(int j=i+;j<=;j++) if(a[j]==) break;
else{
for(int k=i;k<=j;k++) a[k]--;
dfs(x+);
for(int k=i;k<=j;k++) a[k]++;
}
}
for(int i=;i<=;i++){
if(a[i]<||a[i+]<) continue;
for(int j=i+;j<=;j++) if(a[j]<) break;
else{
for(int k=i;k<=j;k++) a[k]-=;
dfs(x+);
for(int k=i;k<=j;k++) a[k]+=;
}
}
for(int i=;i<=;i++){
if(a[i]<) continue;
for(int j=i+;j<=;j++) if(a[j]<) break;
else{
for(int k=i;k<=j;k++) a[k]-=;
dfs(x+);
for(int k=i;k<=j;k++) a[k]+=;
}
}
} int main(){
freopen("landlords.in","r",stdin);
freopen("landlords.out","w",stdout);
int cas; cin>>cas>>n;
while(cas--){
memset(a,,sizeof(a));
for(int i=;i<=n;i++){
int x,k; scanf("%d%d",&x,&k);
if(x<){if(x==) x=; else if(x==) x=; else x=;}
x=+(x-+N)%N; a[x]++;
}
ans=; dfs();
printf("%d\n",ans);
}
}
【NOIP2015提高组】 Day1 T3 斗地主的更多相关文章
- NOIP2015 提高组 Day T3 斗地主
题目描述 牛牛最近迷上了一种叫斗地主的扑克游戏.斗地主是一种使用黑桃.红心.梅花.方片的A到K加上大小王的共5张牌来进行的扑克牌游戏.在斗地主中,牌的大小关 系根据牌的数码表示如下:3<4< ...
- Noip2011 提高组 Day1 T3 Mayan游戏
题目描述 Mayan puzzle是最近流行起来的一个游戏.游戏界面是一个 7 行5 列的棋盘,上面堆放着一些方块,方块不能悬空堆放,即方块必须放在最下面一行,或者放在其他方块之上.游戏通关是指在规定 ...
- Noip2015 提高组 Day1
T1神奇的幻方 直通 思路: 制定一个lrow记录上一个数字所在的行数,lcolume记录上一个数字所在的列数,然后根据题目的描述进行更改即可 上代码: #include <iostream&g ...
- noip2015 提高组day1、day2
NOIP201505神奇的幻方 试题描述 幻方是一种很神奇的N∗N矩阵:它由数字 1,2,3,……,N∗N构成,且每行.每列及两条对角线上的数字之和都相同. 当N为奇数时,我们可以通过以下方 ...
- 2012Noip提高组Day1 T3 开车旅行
题目描述 小 A 和小 B 决定利用假期外出旅行,他们将想去的城市从 1 到 N 编号,且编号较小的 城市在编号较大的城市的西边,已知各个城市的海拔高度互不相同,记城市 i 的海拔高度为 Hi,城市 ...
- NOIP2011提高组 Day1 T3 Mayan游戏
题目描述 Mayan puzzle是最近流行起来的一个游戏.游戏界面是一个7行×5列的棋盘,上面堆放着一些方块,方块不能悬空堆放,即方块必须放在最下面一行,或者放在其他方块之上.游戏通关是指在规定的步 ...
- NOIP2015提高组Day1 Message
题目描述 有n个同学(编号为1到n)正在玩一个信息传递的游戏.在游戏里每人都有一个固定的信息传递对象,其中,编号为i的同学的信息传递对象是编号为Ti同学. 游戏开始时,每人都只知道自己的生日.之后每一 ...
- 洛谷 3953 NOIP2017提高组Day1 T3 逛公园
[题解] 先建反向图,用dijkstra跑出每个点到n的最短距离dis[i] 设f[u][k]表示dis(u,n)<=mindis(u,n)+k的方案数.对于边e(u,v,w),走了这条边的话需 ...
- 【题解】NOIP2015提高组 复赛
[题解]NOIP2015提高组 复赛 传送门: 神奇的幻方 \([P2615]\) 信息传递 \([P2661]\) 斗地主 \([P2668]\) 跳石头 \([P2678]\) 子串 \([P26 ...
- 2015 Noip提高组 Day1
P2615 神奇的幻方 [题目描述] 幻方是一种很神奇的N*N矩阵:它由数字1,2,3,……,N*N构成,且每行.每列及两条对角线上的数字之和都相同. 当N为奇数时,我们可以通过以下方法构建一个幻方: ...
随机推荐
- 201521123039 《java程序设计》第一周学习总结(新）
1.本章学习总结 -Java是面向对象的程序语言,它一切定义都是对象.我们所编写的Java程序经过编译后生成了.class的文件,再经过JVM对.class解释运行就可以得到Java程序,所以Java ...
- 201521123067 《Java程序设计》第12周学习总结
201521123067 <Java程序设计>第12周学习总结 1. 本周学习总结 1.1 以你喜欢的方式(思维导图或其他)归纳总结多流与文件相关内容. 2. 书面作业 将Student对 ...
- 在linux下通过hexdump生成一个十六进制的文本保存文件，解析此文件转变成正常源代码文件。
举例说明: 此十六进制保存的文件为此源代码hexdump生成的: #include<stdio.h> #include<string.h> #include<stdlib ...
- hdu 6197 array array array
array array array Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others ...
- Servlet第七篇【Cookie和Session的区别、应用】
Session和Cookie的区别 从存储方式上比较 Cookie只能存储字符串,如果要存储非ASCII字符串还要对其编码. Session可以存储任何类型的数据,可以把Session看成是一个容器 ...
- ExtJS4为form表单必填项添加红色*标识
通常情况下,ExtJS4的form表单必填项在输入状态下会有特殊提示,非输入状态下,显示却和其他项没有任何区别.为使必填项更加容易区分,我们需要根据allowBlank的属性值,为form表单中的必填 ...
- Sublime Text 3 全程详细图文原创教程
Sublime Text 3 全程详细图文原创教程(持续更新中...) 一. 前言 使用Sublime Text 也有几个年头了,版本也从2升级到3了,但犹如寒天饮冰水,冷暖尽自知.最初也是不知道从何 ...
- angularui 分页
分页组件的使用 <!DOCTYPE html> <html lang="en" ng-app="myApp"> <head> ...
- angular $observe() 和$watch的区别
1.$observe()是属性attributes的方法,只能在DOM属性的值发生变化时用,并且只用于directive内. 当需要监听一个包含变量的属性值时attr1="Name:{{na ...
- [js高手之路] html5 canvas系列教程 - 认识canvas以及基本使用方法
canvas是html5中引入的一个新元素,俗称画布,既然是画布,当然是用来画图的.canvas技术指的是利用javascript操作canvas元素绘制图形的技术,要使用canvas,一定要浏览器支 ...