polya/burnside 学习

参考链接：

http://www.cnblogs.com/hankers/archive/2012/08/03/2622231.html

http://blog.csdn.net/raalghul/article/details/51767941

首先来说说burnside引理是什么。

一天你正在刷题，看到一道关于染色的问题，你认为是一个傻逼题，然后认真一看题目上面写着旋转、翻转后相同的计算一次......你立刻就傻眼了。

接下来是科普时间。

首先我们考虑什么东西叫置换，例如(1,2,3,4,5)->(2,1,4,5,3)就是一个置换，1喂进去会变成2，3喂进去会变成4，喂进去一个(5,4,3,2,1)会变成(3,5,4,1,2)。

老司机们可能会把它写成这样：

$\begin{pmatrix}1&2&3&4&5\\2&1&4&5&3\end{pmatrix}\\$

例如现在三角形有三个顶点123，那么旋转本质上就是置换:(1,2,3)->(2,3,1)和(1,2,3)->(3,1,2)。

那么burnside引理就是对于k个置换，设在每个置换的作用下保持不变的染色方案为z1...zk，那么在置换意义下不同的染色方案一共有(z1+z2+...+zk)/k种。

应用的时候需要注意，例如转一次和转两次这两个置换都需要考虑，以及本身也是一个置换。

举个老例子，4个格子排成2*2的正方形，用两种颜色染色，旋转之后相同的算同一种，求不同染色方案数。

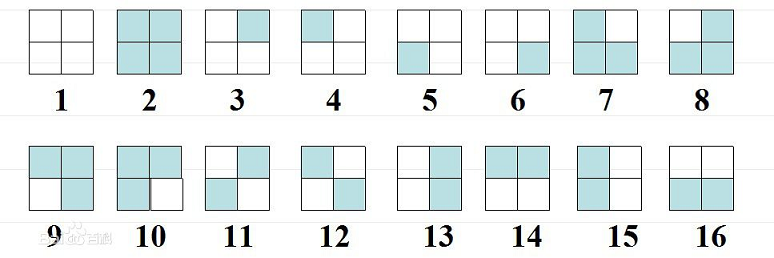
置换有四个：不动、转90°、转180°、转270°，在这些置换下不变的方案数共有16、2、4、2种，由burnside原理可以知道有(16+2+4+2)/4=6种方案。

接下来讲polya定理。首先，每个置换都可以被分解成若干不相交循环的乘积，什么意思呢？

例如上面的那个置换，我们注意到1->2->1，3->4->5->3，所以就可以写成(12)(345)，(12)、(345)就叫循环。

我们发现在每个置换的作用下保持不变的染色方案，每个循环必须染一样的颜色，所以可以发现z就等于颜色数^循环节个数。

对应到上面那个题目，我们先把正方形四个格子按从左到右从上到下1234编号。

不动：(1)(2)(3)(4)。转90°：(1234)。转180°：(13)(24)。转270°：(1432)。

那么一共也是有(2^4+2^1+2^2+2^1)/4=6种方案。

例1 poj2409

用c种颜色染一个长度为s的环，旋转翻转之后相同的算同一种，求方案数，cs<=32（似乎只是为了保证答案不会太大）。

暴力硬上吧。由于某些原因，置换的循环节我都是用并查集找的你来打我啊

#include <iostream>
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <time.h>
#include <stdlib.h>
#include <string>
#include <bitset>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <algorithm>
#include <sstream>
#include <stack>
#include <iomanip>
using namespace std;
#define pb push_back
#define mp make_pair
typedef pair<int,int> pii;
typedef long long ll;
typedef double ld;
typedef vector<int> vi;
#define fi first
#define se second
#define fe first
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define Edg int M=0,fst[SZ],vb[SZ],nxt[SZ];void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}void adde(int a,int b){ad_de(a,b);ad_de(b,a);}
#define Edgc int M=0,fst[SZ],vb[SZ],nxt[SZ],vc[SZ];void ad_de(int a,int b,int c){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}void adde(int a,int b,int c){ad_de(a,b,c);ad_de(b,a,c);}
#define es(x,e) (int e=fst[x];e;e=nxt[e])
#define VIZ {printf("digraph G{\n"); for(int i=1;i<=n;i++) for es(i,e) printf("%d->%d;\n",i,vb[e]); puts("}");}
#ifdef LOCAL
#define TIMER cerr<<clock()<<"ms\n"
#else
#define TIMER
#endif
#define SZ 666666
int ff[SZ];
void init(int n)
{
    for(int i=0;i<=n;i++) ff[i]=-1;
}
int gf(int x)
{
    return (ff[x]==-1)?x:ff[x]=gf(ff[x]);
}
void uni(int a,int b)
{
    int ga=gf(a),gb=gf(b);
    if(ga^gb) ff[ga]=gb;
}
ll qpl(ll a,ll b)
{
    ll ans=1;
    while(b)
    {
        if(b&1) ans=ans*a;
        a=a*a; b>>=1;
    }
    return ans;
}
ll query(int c,int s)
{
    ll ans=0;
    for(int i=0;i<s;i++)
    {
        init(s);
        for(int j=0;j<s;j++) uni(j,(j+i)%s);
        int xh=0;
        for(int j=0;j<s;j++) xh+=gf(j)==j;
        ans+=qpl(c,xh);
    }
    for(int i=1;i<=s;i++)
    {
        init(s);
        for(int j=0;j<s;j++) uni(j,((i-j)%s+s)%s);
        int xh=0;
        for(int j=0;j<s;j++) xh+=gf(j)==j;
        ans+=qpl(c,xh);
    }
    return ans/(s*2);
}
int main()
{
    int c,s;
    while(1)
    {
        cin>>c>>s;
        if(c==0&&s==0) break;
        cout<<query(c,s)<<"\n";
    }
}

然后这种做法显然过于暴力了，我们发现旋转k个位置之后的循环节就是gcd(s,k)，翻转的话，如果奇数就是每个点到对边这样s个置换，每个置换循环节都是(s+1)/2，如果偶数就是对顶点和对边这样各s/2个，对顶点的循环节是s/2+1，对边的是s/2+1。

#include <iostream>
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <time.h>
#include <stdlib.h>
#include <string>
#include <bitset>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <algorithm>
#include <sstream>
#include <stack>
#include <iomanip>
using namespace std;
#define pb push_back
#define mp make_pair
typedef pair<int,int> pii;
typedef long long ll;
typedef double ld;
typedef vector<int> vi;
#define fi first
#define se second
#define fe first
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define Edg int M=0,fst[SZ],vb[SZ],nxt[SZ];void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}void adde(int a,int b){ad_de(a,b);ad_de(b,a);}
#define Edgc int M=0,fst[SZ],vb[SZ],nxt[SZ],vc[SZ];void ad_de(int a,int b,int c){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}void adde(int a,int b,int c){ad_de(a,b,c);ad_de(b,a,c);}
#define es(x,e) (int e=fst[x];e;e=nxt[e])
#define VIZ {printf("digraph G{\n"); for(int i=1;i<=n;i++) for es(i,e) printf("%d->%d;\n",i,vb[e]); puts("}");}
#ifdef LOCAL
#define TIMER cerr<<clock()<<"ms\n"
#else
#define TIMER
#endif
#define SZ 666666
int ff[SZ];
void init(int n)
{
    for(int i=0;i<=n;i++) ff[i]=-1;
}
int gf(int x)
{
    return (ff[x]==-1)?x:ff[x]=gf(ff[x]);
}
void uni(int a,int b)
{
    int ga=gf(a),gb=gf(b);
    if(ga^gb) ff[ga]=gb;
}
ll qpl(ll a,ll b)
{
    ll ans=1;
    while(b)
    {
        if(b&1) ans=ans*a;
        a=a*a; b>>=1;
    }
    return ans;
}
ll query(int c,int s)
{
    ll ans=0;
    for(int i=1;i<=s;i++)
        ans=ans+qpl(c,__gcd(s,i));
    int a,b;
    if(s&1) a=s,b=0;
    else a=b=s/2;
    ans+=a*qpl(c,s/2+1);
    ans+=b*qpl(c,s/2);
    return ans/(s*2);
}
int main()
{
    int c,s;
    while(1)
    {
        cin>>c>>s;
        if(c==0&&s==0) break;
        cout<<query(c,s)<<"\n";
    }
}

（gcd懒得写了，就用__gcd了）

例2 uestc75/tju2795 The Queen's New Necklaces

有一串项链用若干种颜色染色，第i种颜色有mi个，旋转相同的不计，问有多少种不同的项链。

我们考虑枚举旋转i个珠子之后不动的方案数，那么就会有gcd(n,i)个循环节，然后我们设p=n/gcd(n,i)为每个循环节的长度，那么如果有颜色数量不是p的倍数显然不可能有不动的，否则每个循环节颜色要一样，就随便统计一下就是了。

高精度懒得写，就不贴代码了。

例3 poj2154 color

用不超过n种颜色给一个长度为n的环染色，旋转相同的不计，求方案数mod P。n<=10^9，3500组数据。

似乎比例1还水，不过n这么大，显然需要优化。

ll ans=0;
for(int i=1;i<=n;i++)
    ans=ans+qpl(n,__gcd(n,i));
return ans/n;

这是例1关于旋转那部分的代码，那么我们需要优化的实际上就是：$\sum_{i=1}^nn^{(i,n)}$

查询oeis可以发现：http://oeis.org/A228640

我们枚举(i,n)的gcd，那么(i/gcd,n/gcd)=1，所以对答案的贡献就是$\varphi(\frac{n}{gcd})*n^{gcd}$。

那么我们就得到了oeis上的这个公式：$\sum_{d|n}{\varphi(d)*n^{\frac{n}{d}}}$

然后我们发现这个式子似乎不是很好搞......

那么我们不妨枚举n的因数d，暴力算欧拉函数（拿所有质数筛一筛），这样效率应该还挺高的。

因为最后我们没办法除以n，所以算次方的时候要人工-1。

（由于懒没有写qaq有空写吧）