奇怪吸引子---TreeScrollUnifiedChaoticSystem
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性、稳定性、吸引性。吸引子是一个数学概念,描写运动的收敛类型。它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出发的非定常流的所有轨道都趋于它,这样的集合有很复杂的几何结构。由于奇怪吸引子与混沌现象密不可分,深入了解吸引子集合的性质,可以揭示出混沌的规律。
这里会展示利用奇怪吸引子生成的艺术图像。奇怪吸引子通常含有三维或四维的数据,而图像是二维的,因此可以从不同的位面将奇怪吸引子投影到二维图像中。
原图及数学公式取自:
http://chaoticatmospheres.com/125670/1204030/gallery/strange-attractors


这里使用自己定义语法的脚本代码生成混沌图像,相关软件参见:YChaos生成混沌图像。如果你对数学生成图形图像感兴趣,欢迎加入QQ交流群: 367752815。
脚本代码:
[ScriptLines]
u=a*(j - i) + c*i*k
v=e*i - i*k
w=b*k + i*j - d*i*i
i=i+u*t
j=j+v*t
k=k+w*t
x=i
y=j [Variables]
a=50.000000
b=0.890200
c=0.500600
d=0.607000
e=20.000000
i=0.100000
j=0.100000
k=0.100000
t=0.001000
混沌图像:
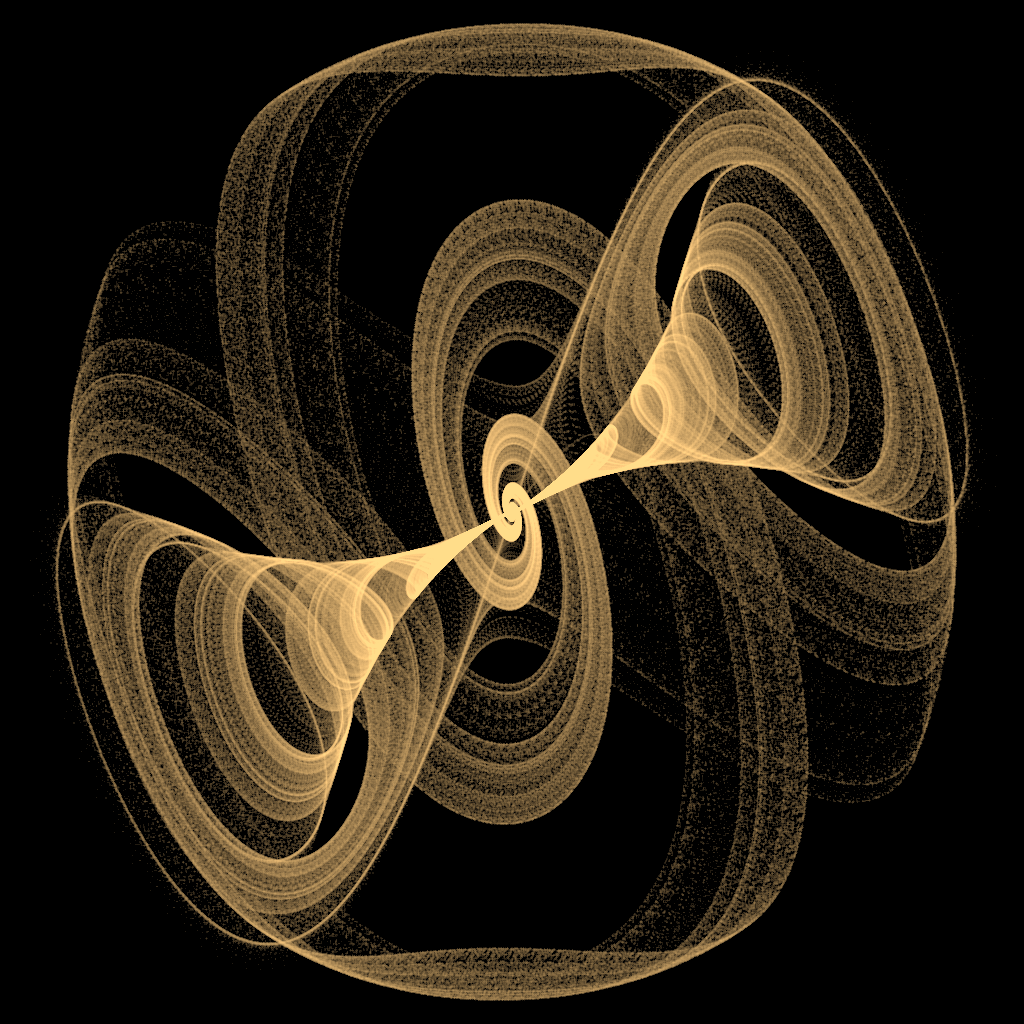
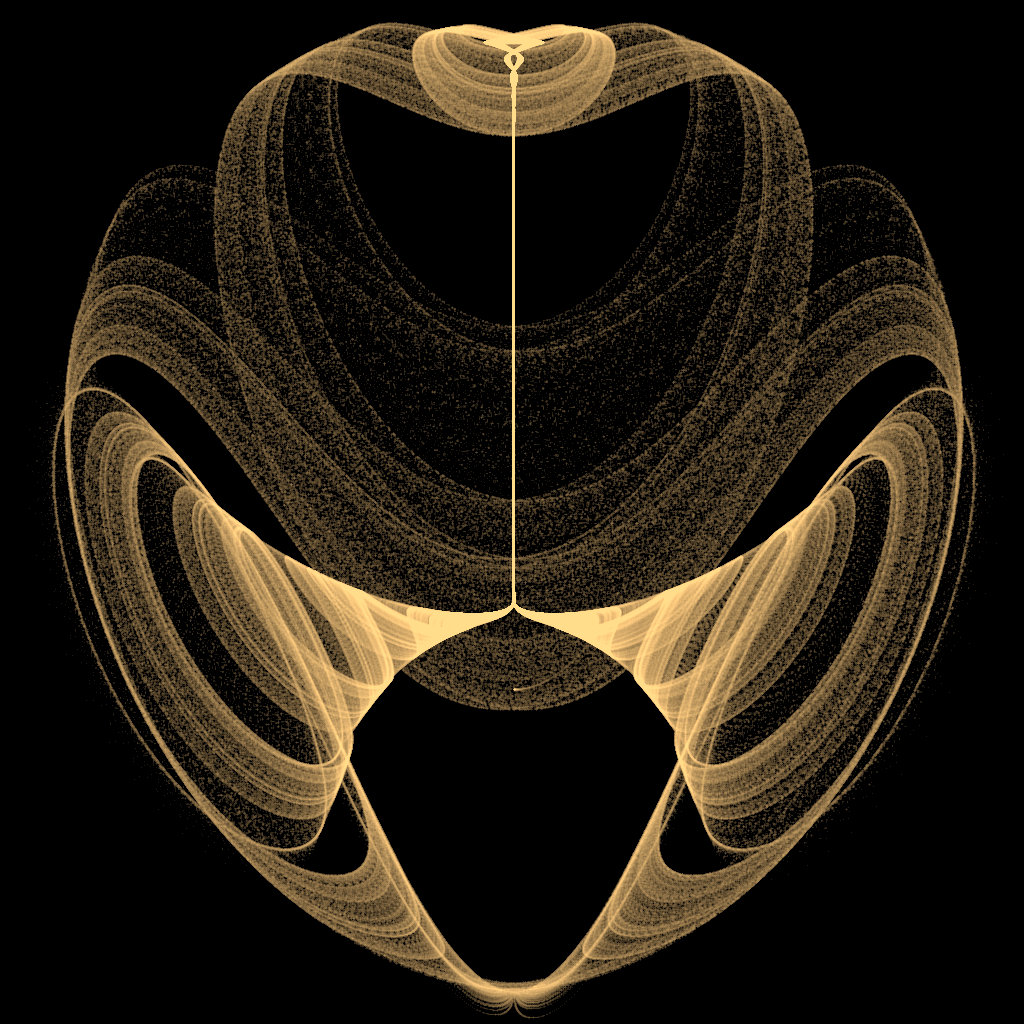
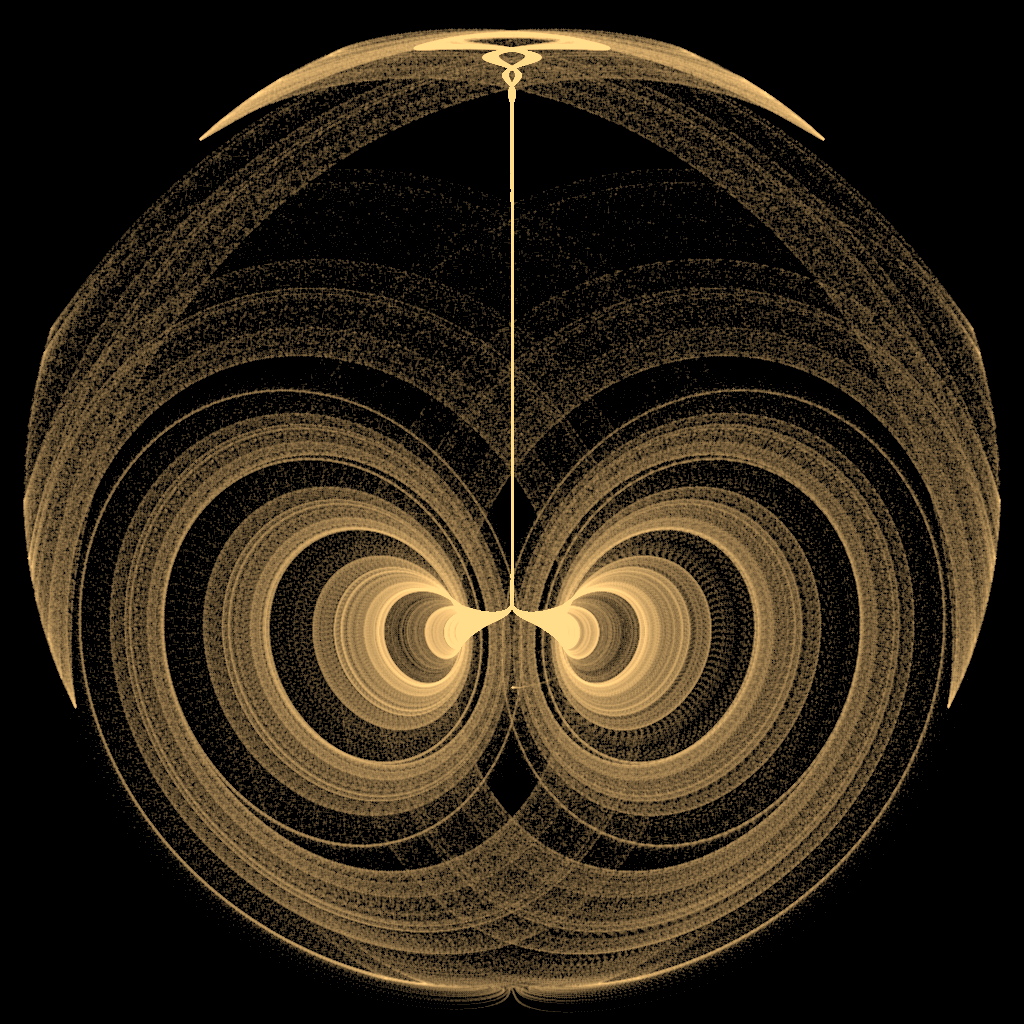
奇怪吸引子---TreeScrollUnifiedChaoticSystem的更多相关文章
- 奇怪吸引子---YuWang
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---WimolBanlue
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---WangSun
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Thomas
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---ShimizuMorioka
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Sakarya
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Russler
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Rucklidge
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---RayleighBenard
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
随机推荐
- Browser增加下载路径选择功能
SWE Browser中有xml/download_settings_preferences.xml, 但在代码中却没有调用,导致“设置”中没有”选择下载路径“功能. 在com.android.bro ...
- windows all version - 实现指定路径共享
调用API函数NetShareAdd()将文件夹设置为共享,调用此函数后如果不做其他设置,网络用户是无法访问共享文件夹的,因为此文件夹在NTFS分区中,同时受到NTFS文件系统的访问控制,因此还需要第 ...
- 亲子之间,在于看懂,无关耐心zz
每当有人告诉我:『你对孩子真有耐心!』时,我总会想起我的金项链,当越来越多人说的时候,我就越想找出来,我翻箱倒柜的找,越心急却越找不到,那 一条金项链从我十八岁那一年一直戴在我的脖子上一直到女儿两岁, ...
- Hadoop MapReduce编程创建maven项目时所用到的pom依赖
<dependency> <groupId>junit</groupId> <artifactId>junit</artifactId> & ...
- Mysql --分区表(6)Hash分区
HASH分区 HASH分区主要用来分散热点读,确保数据在预先确定个数的分区中尽可能平均分布.对一个表执行HASH分区时,MySQL会对分区键应用一个散列函数,以此确定数据应当放在N个分区中的哪个分区 ...
- Wordpress编辑器(Tinymce)在Chrome中动态修改图片大小
Chrome不支持tinymce中图片动态修改大小,可以在theme的functions.php中加入下面代码在Tinymce中模拟这一功能: function tinymce_editor_sett ...
- java基础-反射之Class.forName
Class.forName 查阅javaAPI public static Class<?> forName(String className) throws ClassNotFoundE ...
- D3 学习资源
发现这个网站还是挺不错的:http://www.ourd3js.com/wordpress/
- python递归次数和堆栈溢出问题
在做递归的时候,测试了一下python的递归能力. 如果不设置递归次数的话,大概只能在992次左右,就会出现错误:RuntimeError: maximum recursion depth excee ...
- 【基础知识】.Net基础加强11天
一. 扩展方法 1. 声明扩展方法的步骤: 1> 类必须是static,方法是static ,第一个参数是被扩展的对象,前面标注(this 数据类型参数名). 2> 使用扩展方法的时候必须 ...
