线段树 Interval Tree

一、线段树

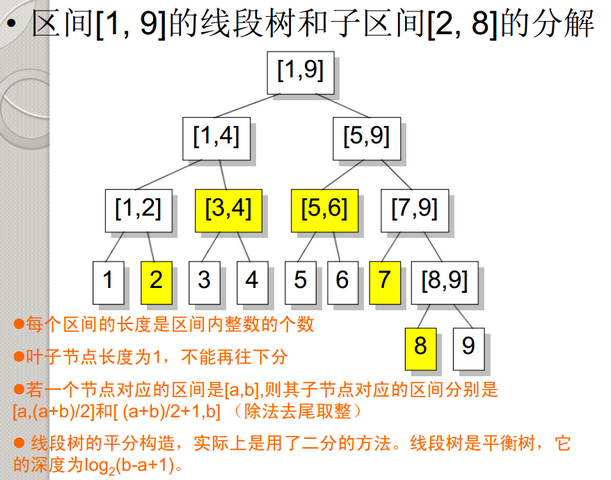
线段树既是线段也是树，并且是一棵二叉树，每个结点是一条线段,每条线段的左右儿子线段分别是该线段的左半和右半区间，递归定义之后就是一棵线段树。

例题：给定N条线段，{[2, 5], [4, 6], [0, 7]}, M个点{2, 4, 7},判断每个点分别在几条线段出现过？

1、构建线段树

2、处理线段

三条线段分割之后

3、查询

对于每一个值我们就可以开始遍历这一颗线段树，加上对于结点的count字段便是在线段中出现的次数

比如对于4，首先遍历[0, 7]，次数 = 0+1=1；4在右半区间，遍历[4, 7],次数 = 1+0=0;4在[4, 7]左半区间, 次数 = 1+2=3;4在[4, 5]左半区间,次数 = 3+0 = 4，遍历结束，次数 = 3说明4在三条线段中出现过,同理可求其他的值，这一步的时间复杂度为O(M*log(MAX-MIN))

二、线段树的存储数据结构

储一颗线段树和二叉树有点类似，需要左孩子和右孩子节点，另外，为了存储每条线段出现的次数，所以一般会加上计数的元素。

struct Node         // 线段树
{
    int left;
    int right;
    int counter;
}segTree[*BORDER]; 

三、线段树支持的操作

一颗线段树至少支持以下四个操作：

• void construct(int index, int lef, int rig)，构建线段树 根节点开始构建区间[lef,rig]的线段树
• void insert(int index, int start, int end)，插入线段[start,end]到线段树, 同时计数区间次数
• int query(int index, int x)，查询点x的出现次数，从根节点开始到[x,x]叶子的这条路径中所有点计数相加方为x出现次数
• void delete_ (int c , int d, int index)，从线段树中删除线段[c,d]

四、线段树的特征

1、线段树的深度不超过logL（L是最长区间的长度）

2、线段树把区间上的任意一条线段都分成不超过2logL条线段。

线段树能在O(logL)的时间内完成一条线段的插入、删除、查找等工作。

五、线段树的应用

线段树适用于和区间统计有关的问题。比如某些数据可以按区间进行划分，按区间动态进行修改，而且还需要按区间多次进行查询，那么使用线段树可以达到较快查询速度。

(1)：区间最值查询问题 （见模板1）

(2)：连续区间修改或者单节点更新的动态查询问题 （见模板2）

(3)：多维空间的动态查询 （见模板3）

六、模板代码

模板1：

RMQ，查询区间最值下标---min

#include<iostream>    

using namespace std;    

#define MAXN 100
#define MAXIND 256 //线段树节点个数    

//构建线段树,目的:得到M数组.
void build(int node, int b, int e, int M[], int A[])
{
    if (b == e)
        M[node] = b; //只有一个元素,只有一个下标
    else
    {
        build( * node, b, (b + e) / , M, A);
        build( * node + , (b + e) /  + , e, M, A);    

        if (A[M[ * node]] <= A[M[ * node + ]])
            M[node] = M[ * node];
        else
            M[node] = M[ * node + ];
    }
}    

//找出区间 [i, j] 上的最小值的索引
int query(int node, int b, int e, int M[], int A[], int i, int j)
{
    int p1, p2;    

    //查询区间和要求的区间没有交集
    if (i > e || j < b)
        return -;    

    if (b >= i && e <= j)
        return M[node];    

    p1 = query( * node, b, (b + e) / , M, A, i, j);
    p2 = query( * node + , (b + e) /  + , e, M, A, i, j);    

    //return the position where the overall
    //minimum is
    if (p1 == -)
        return M[node] = p2;
    if (p2 == -)
        return M[node] = p1;
    if (A[p1] <= A[p2])
        return M[node] = p1;
    return M[node] = p2;    

}    

int main()
{
    int M[MAXIND]; //下标1起才有意义,否则不是二叉树,保存下标编号节点对应区间最小值的下标.
    memset(M,-,sizeof(M));
    int a[]={,,,,,,,,,};
    build(, , sizeof(a)/sizeof(a[])-, M, a);
    cout<<query(, , sizeof(a)/sizeof(a[])-, M, a, , )<<endl;
    return ;
}  

模板2：

连续区间修改或者单节点更新的动态查询问题 （此模板查询区间和）

#include <cstdio>
#include <algorithm>
using namespace std;    

#define lson l , m , rt << 1
#define rson m + 1 , r , rt << 1 | 1
#define root 1 , N , 1
#define LL long long
const int maxn = ;
LL add[maxn<<];
LL sum[maxn<<];
void PushUp(int rt) {
    sum[rt] = sum[rt<<] + sum[rt<<|];
}
void PushDown(int rt,int m) {
    if (add[rt]) {
        add[rt<<] += add[rt];
        add[rt<<|] += add[rt];
        sum[rt<<] += add[rt] * (m - (m >> ));
        sum[rt<<|] += add[rt] * (m >> );
        add[rt] = ;
    }
}
void build(int l,int r,int rt) {
    add[rt] = ;
    if (l == r) {
        scanf("%lld",&sum[rt]);
        return ;
    }
    int m = (l + r) >> ;
    build(lson);
    build(rson);
    PushUp(rt);
}
void update(int L,int R,int c,int l,int r,int rt) {
    if (L <= l && r <= R) {
        add[rt] += c;
        sum[rt] += (LL)c * (r - l + );
        return ;
    }
    PushDown(rt , r - l + );
    int m = (l + r) >> ;
    if (L <= m) update(L , R , c , lson);
    if (m < R) update(L , R , c , rson);
    PushUp(rt);
}
LL query(int L,int R,int l,int r,int rt) {
    if (L <= l && r <= R) {
        return sum[rt];
    }
    PushDown(rt , r - l + );
    int m = (l + r) >> ;
    LL ret = ;
    if (L <= m) ret += query(L , R , lson);
    if (m < R) ret += query(L , R , rson);
    return ret;
}
int main() {
    int N , Q;
    scanf("%d%d",&N,&Q);
    build(root);
    while (Q --) {
        char op[];
        int a , b , c;
        scanf("%s",op);
        if (op[] == 'Q') {
            scanf("%d%d",&a,&b);
            printf("%lld\n",query(a , b ,root));
        } else {
            scanf("%d%d%d",&a,&b,&c);
            update(a , b , c , root);
        }
    }
    return ;
}    

模板3：

多维空间的动态查询

（留待填充）

模板4：用指针构建的线段树

#include <iostream>
using namespace std;
struct Line{
  int left, right, count;
  Line *leftChild, *rightChild;
  Line(int l, int r): left(l), right(r) {}
};

//建立一棵空线段树
void createTree(Line *root) {
  int left = root->left;
  int right = root->right;
  if (left < right) {
    int mid = (left + right) / ;
    Line *lc =  new Line(left, mid);
    Line *rc =  new Line(mid + , right);
    root->leftChild = lc;
    root->rightChild = rc;
    createTree(lc);
    createTree(rc);
  }
}

//将线段[l, r]分割
void insertLine(Line *root, int l, int r) {
  cout << l << " " << r << endl;
  cout << root->left << " " << root->right << endl << endl;
  if (l == root->left && r == root->right) {
    root->count += ;
  } else if (l <= r) {
    int rmid = (root->left + root->right) / ;
    if (r <= rmid) {
      insertLine(root->leftChild, l, r);
    } else if (l >= rmid + ) {
      insertLine(root->rightChild, l, r);
    } else {
      int mid = (l + r) / ;
      insertLine(root->leftChild, l, mid);
      insertLine(root->rightChild, mid + , r);
    }
  }
}
//树的中序遍历（测试用）
void inOrder(Line* root) {
  if (root != NULL) {
    inOrder(root->leftChild);
    printf("[%d, %d], %d\n", root->left, root->right, root->count);
    inOrder(root->rightChild);
  }
}

//获取值n在线段上出现的次数
int getCount(Line* root, int n) {
  int c = ;
  if (root->left <= n&&n <= root->right)
    c += root->count;
  if (root->left == root->right)
    return c;
  int mid = (root->left + root->right) / ;
  if (n <= mid)
    c += getCount(root->leftChild, n);
  else
    c += getCount(root->rightChild, n);
  return c;
}
int main() {
  int l[] = {, , };
  int r[] = {, , };
  int MIN = l[];
  int MAX = r[];
  for (int i = ; i < ; ++i) {
    if (MIN > l[i]) MIN = l[i];
    if (MAX < r[i]) MAX = r[i];
  }
  Line *root = new Line(MIN, MAX);
  createTree(root);
  for (int i = ; i < ; ++i) {
    insertLine(root, l[i], r[i]);
  }
  inOrder(root);
  int N;
  while (cin >> N) {
    cout << getCount(root, N) << endl;
  }
  return ;
}

七、ACM题

在代码前先介绍一些线段树风格:

• maxn是题目给的最大区间,而节点数要开4倍,确切的来说节点数要开大于maxn的最小2^x的两倍
• lson和rson分辨表示结点的左儿子和右儿子,由于每次传参数的时候都固定是这几个变量,所以可以用预定于比较方便的表示
• 以前的写法是另外开两个个数组记录每个结点所表示的区间,其实这个区间不必保存,一边算一边传下去就行,只需要写函数的时候多两个参数,结合lson和rson的预定义可以很方便
• PushUP(int rt)是把当前结点的信息更新到父结点
• PushDown(int rt)是把当前结点的信息更新给儿子结点
• rt表示当前子树的根(root),也就是当前所在的结点

整理这些题目后我觉得线段树的题目整体上可以分成以下四个部分:

（1）单点更新:

最最基础的线段树,只更新叶子节点,然后把信息用PushUP(int r)这个函数更新上来

hdu1166 敌兵布阵

题意:O(-1)

思路:O(-1)

线段树功能:update:单点增减 query:区间求和

code 1:

#include<cstring>
#include<iostream>  

#define M 50005
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
/*left,right,root,middle*/  

int sum[M<<];  

inline void PushPlus(int rt)
{
    sum[rt] = sum[rt<<] + sum[rt<<|];
}  

void Build(int l, int r, int rt)
{
    if(l == r)
    {
        scanf("%d", &sum[rt]);
        return ;
    }
    int m = ( l + r )>>;  

    Build(lson);
    Build(rson);
    PushPlus(rt);
}  

void Updata(int p, int add, int l, int r, int rt)
{  

    if( l == r )
    {
        sum[rt] += add;
        return ;
    }
    int m = ( l + r ) >> ;
    if(p <= m)
        Updata(p, add, lson);
    else
        Updata(p, add, rson);  

    PushPlus(rt);
}  

int Query(int L,int R,int l,int r,int rt)
{
    if( L <= l && r <= R )
    {
        return sum[rt];
    }
    int m = ( l + r ) >> ;
    int ans=;
    if(L<=m )
        ans+=Query(L,R,lson);
    if(R>m)
        ans+=Query(L,R,rson);  

    return ans;
}
int main()
{
    int T, n, a, b;
    scanf("%d",&T);
    for( int i = ; i <= T; ++i )
    {
        printf("Case %d:\n",i);
        scanf("%d",&n);
        Build(,n,);  

        char op[];  

        while( scanf("%s",op) &&op[]!='E' )
        {  

            scanf("%d %d", &a, &b);
            if(op[] == 'Q')
                printf("%d\n",Query(a,b,,n,));
            else if(op[] == 'S')
                Updata(a,-b,,n,);
            else
                Updata(a,b,,n,);  

        }
    }
    return ;
}  

code 2：

#include <iostream>
#include <cstdio>

using namespace std;

const int NMAX = ;
int n;
int a[NMAX];
struct Node {
    int left, right, sum;
};
Node node[*NMAX];

void push_up(int pos) {
    node[pos].sum = node[pos<<].sum + node[(pos<<)+].sum;
}

void build(int left, int right, int pos) {
    node[pos].left = left;
    node[pos].right = right;
    if (left == right) {
        node[pos].sum = a[left];
        return;
    }
    int mid = (left + right) >> ;
    build(left, mid, pos<<);
    build(mid+, right, (pos<<)+);
    push_up(pos);
}

void update(int index, int val, int pos) {
    if (node[pos].left == node[pos].right) {
        node[pos].sum += val;
        return;
    }
    int mid = (node[pos].left + node[pos].right) >> ;
    if (index <= mid) update(index, val, pos<<);
    else update(index, val, (pos<<)+);
    push_up(pos);
}

int query(int left, int right, int pos) {
    if (node[pos].left == left && node[pos].right == right) return node[pos].sum;
    int mid = (node[pos].left + node[pos].right) >> ;
    if (left > mid) return query(left, right, (pos<<)+);
    else if (right <= mid) return query(left, right, pos<<);
    else return query(left, mid, pos<<) + query(mid+, right, (pos<<)+);
}

int main()
{
    int T;
    scanf("%d", &T);
    for (int i=; i<T; i++) {
        scanf("%d", &n);
        for (int j=; j<=n; j++) {
            scanf("%d", a+j);
        }

        printf("Case %d:\n", i+);
        build(, n, );
        getchar();
        int x, y;
        char cs[];
        while (scanf("%s",cs) && cs[] != 'E') {
            scanf("%d%d%*c", &x, &y);
            if (cs[] == 'Q') printf("%d\n", query(x, y, ));
            else if (cs[] == 'A') update(x, y, );
            else update(x, -y, );
        }
    }
    return ;
}

 

八、Reference：

1、菜鸟都能理解的线段树入门经典

2、【完全版】线段树 http://www.notonlysuccess.com/index.php/segment-tree-complete/

3、线段树(segment tree)

4、数据结构：线段树

5、数据结构专题——线段树

6、线段树专题【暂停更新中】