重磅丨腾讯云开源业界首个 etcd 一站式治理平台 Kstone

Kstone 开源

在 CNCF 云原生基金会举办的2021年12月9日 KubeCon China大会上，腾讯云容器 TKE 团队发布了 Kstone etcd 治理平台开源项目。

Kstone 是腾讯云容器TKE团队发起的一个基于 Kubernetes 的云原生一站式 etcd 治理项目。该项目源自腾讯内部大规模 etcd 集群治理和最佳实践，很好的实现了对各类业务场景下的 etcd 集群的可视化管理和运维，极大简化了各类场景的 etcd 运维复杂度，将帮助你及时发现各种潜在的 etcd 集群隐患，显著提高 K8s 和 etcd 集群的稳定性和数据安全性，助力业务更稳更快运行。

Kstone 架构及特性

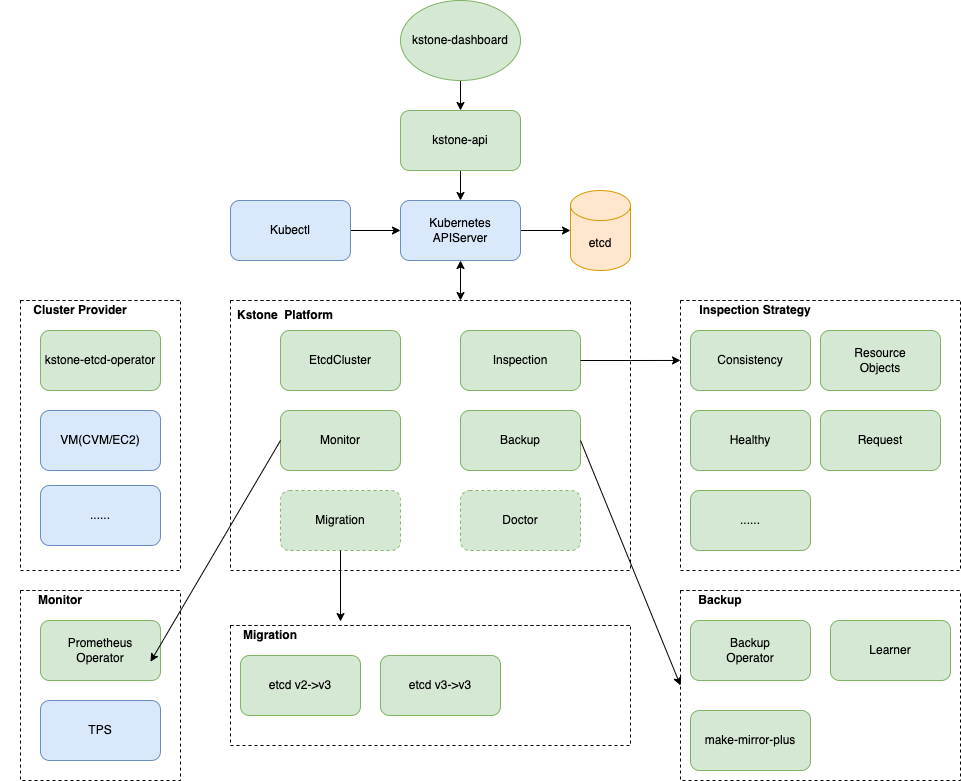
作为一个通用的 etcd 治理开源项目，Kstone 项目拥有诸多特性：

集群管理：Kstone 不仅支持关联已有集群，而且内置了一个高级版的 kstone-etcd-operator, 它将可以帮助你在 K8s 集群上高可靠的部署 etcd 集群。所以，无论你是存量的 Kubernetes 的 etcd 集群管理诉求，还是你希望创建新的 etcd 集群提供给注册中心、APISIX 网关、配置存储等业务场景使用，kstone 都可以实现以上各类场景的 etcd 集群管理。
集群巡检：Kstone 项目沉淀了腾讯内部大规模的etcd集群治理经验，提供了丰富的集群巡检策略，如数据一致性、资源对象数、健康度、热点Key、db满等策略，将帮助你及时发现隐患，提升 etcd 集群稳定性。
数据备份：Kstone 提供分钟级的 etcd 数据备份能力，支持将数据备份到腾讯云 COS 等对象存储。同时，我们还支持通过 kstone-etcd-operator 创建 Learner 实现数据跨城热备。
集群监控：Kstone 支持集群关联和创建时自动开启监控，内置了丰富的 grafana metrics 视图，将帮助你提高定位问题效率。
数据迁移：Kstone 将提供大规模 etcd 集群数据自动迁移能力，并支持多种迁移算法（etcd v2版本到v3版本，etcd v3 版本到 v3 版本，冷迁移，热迁移等）。自动化迁移能力，将帮助你大幅提升集群稳定性。
智能诊断：Kstone 将提供 etcd 集群诊断诊断功能，为你分析集群各类隐患，输出 etcd 专家级优化建议。
可视化：Kstone 提供了一个 web 系统，帮助你轻轻松松完成 etcd 集群管理，涵盖集群管理、监控、巡检、备份、etcd 数据可视化查看。
部署简单：Kstone 提供了 helm 一键部署能力，极大简化了部署复杂度。

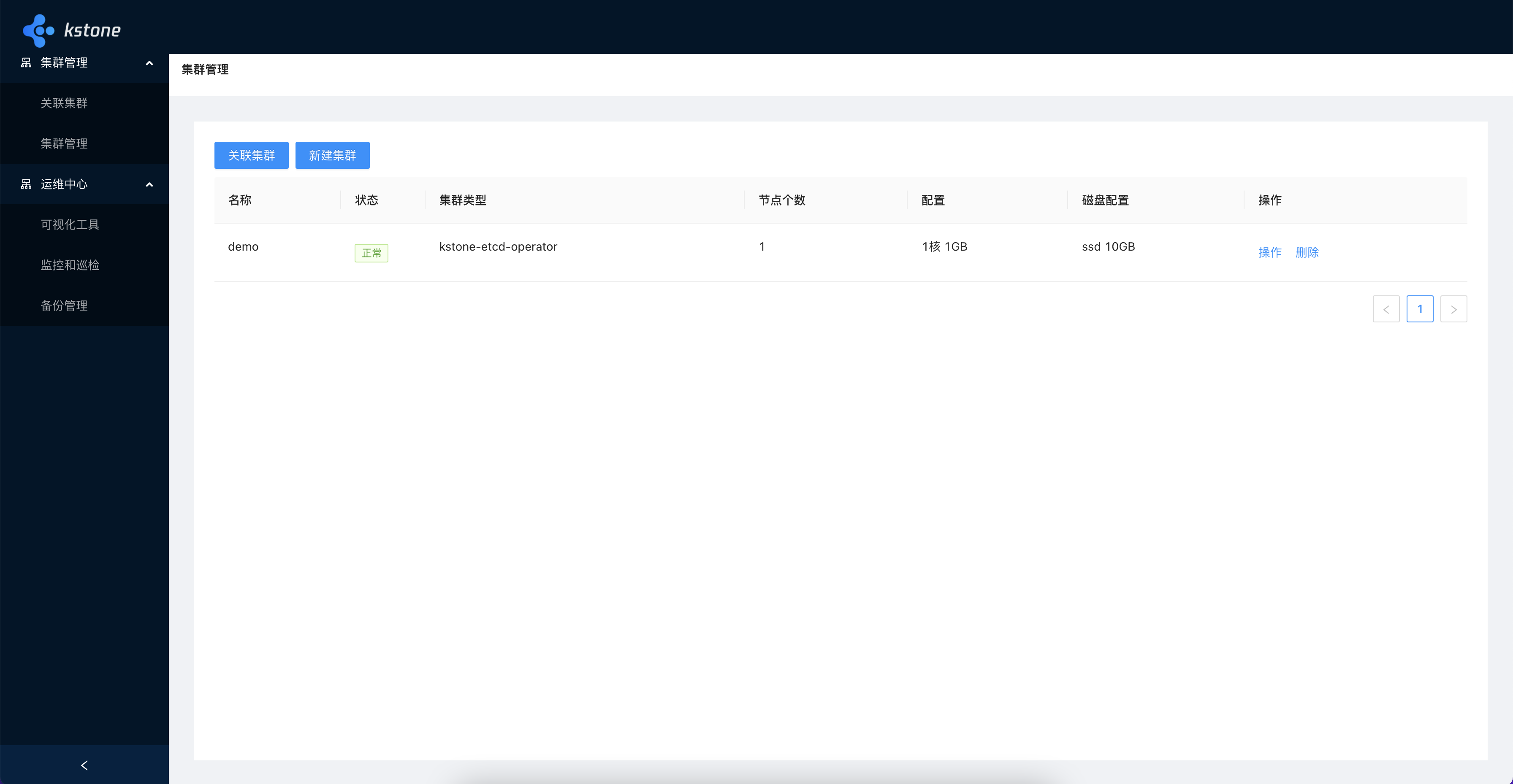
目前，Kstone 已在腾讯云、腾讯会议、腾讯广告、算力平台、腾讯游戏业务等有广泛应用，落地场景覆盖 Kubernetes etcd 集群管理、APISIX 网关、注册中心、配置存储等。

未来，我们将坚信开源、社区、生态、中立、标准的价值，与社区的小伙伴们一起，致力于推进Kstone项目的技术发展和应用落地。

Kstone 正式开源啦！欢迎更多开发爱好者参与！

开源项目 GitHub 地址：

https://github.com/tkestack/kstone

只要你对 Kstone 感兴趣，都欢迎加入，参与方式：添加腾小云(TKEplatform)，回复：Kstone，小云会拉你进群。

关于我们

更多关于云原生的案例和知识，可关注同名【腾讯云原生】公众号~

福利：

①公众号后台回复【手册】，可获得《腾讯云原生路线图手册》&《腾讯云原生最佳实践》~

②公众号后台回复【系列】，可获得《15个系列100+篇超实用云原生原创干货合集》，包含Kubernetes 降本增效、K8s 性能优化实践、最佳实践等系列。

③公众号后台回复【白皮书】，可获得《腾讯云容器安全白皮书》&《降本之源-云原生成本管理白皮书v1.0》

【腾讯云原生】云说新品、云研新术、云游新活、云赏资讯，扫码关注同名公众号，及时获取更多干货！！