fibnacci数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列、因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(1)=1,F(2)=1, F(n)=F(n-1)+F(n-2)(n>=3,n∈N*)

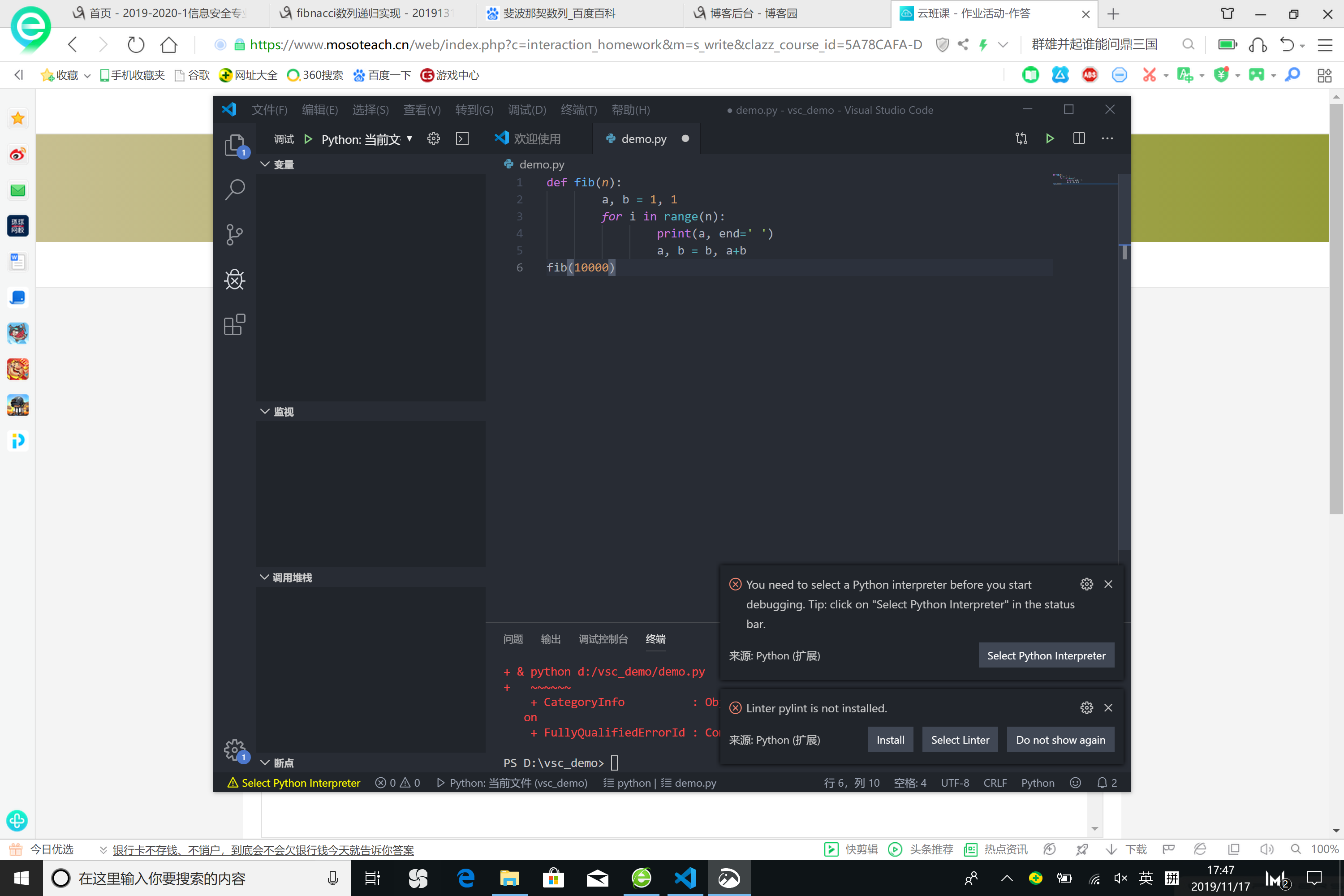
但是无法测试
11.19

一分钟内无法算出fib(10000)
fibnacci数列的更多相关文章
- fibnacci数列的两种实现(递归实现和循环实现)
//一切尽在规律中,认真观察,你会明白更多... using System;using System.Collections.Generic;using System.Linq;using Syste ...
- fibnacci数列递归
1,斐波那契数列(Fibonacci sequence),又称黄金分割数列.因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这 ...
- fibnacci数列递归实现
斐波那契数列 Fibonacci sequence又称黄金分割数列.因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为"兔子数列" ...
- fibnacci数列的python实现
费波那契数列(Successione di Fibonacci) 又译为费波拿契数.斐波那契数列.费氏数列.黄金分割数列 在数学上,费波那契数列是以递归的方法来定义: 用文字来说,就是费波那契数列由0 ...
- 2016 CCPC长春重现赛
1.2016中国大学生程序设计竞赛(长春)-重现赛 2.总结:会做的太少,应变能力也不行,或者说猜题目的能力不行 02 水 04 HDU 5914 Triangle 1.题意:1~n,n个数,问 ...
- Python基础(7)--函数
本篇文章将介绍如何将语句组织成函数,以及参数概念以及在程序中的用途 本文地址:http://www.cnblogs.com/archimedes/p/python-function.html,转载请注 ...
- UML状态图和活动图
UML状态图和活动图 统一建模语言UML(Unified Modeling Language)是非专利的第三代建模和规约语言.UML是一种开放的方法,用于说明.可视化.构建和编写一个正在开发的.面向对 ...
- Python基础-函数(function)
这里我们看看Python中函数定义的语法,函数的局部变量,函数的参数,Python中函数的形参可以有默认值,参数的传递是赋值操作,在函数调用时,可以对实参进行打包和解包 1,函数定义 关键字def引 ...
- 【BestCoder】【Round#29】
T1 啊……a^b 与 c^d比较大小,我们可以两边取对数,转化成 log(a^b)=b*log(a) 和d*log(c) 这样就能直接算了……然后稍微搞一下精度什么的就A了=.= //BC #29 ...
随机推荐
- ViewPager2 使用说明书
ViewPager2 使用说明书 零.Demo 项目源码 演示 apk 如果对你有用,希望能给个 star,谢谢. 一.功能 官方关于使用 ViewPager2 创建滑动视图的说明: Swipe vi ...
- [1.6W字] 浏览器跨域请求限制的详细原理分析&寻找一种最简单的方式实现XHR跨域(9种方法, 附大招可以纯前端实现跨域!)
Title/ 浏览器跨域(CrossOrigin)请求的原理, 以及解决方案详细指南 #flight.Archives011 序: 最近看到又有一波新的创作活动了, 官方给出的话题中有一个" ...
- linux下设备驱动的结构&编译&加载
构造和运行模块 insmod modprobe rmmod 用来装载模块到正运行的内核和移除模块的用户空间工具. #include<linux/init.h> module_init(in ...
- Git脑图
ps:有时我们想一台有不同的git账号对应不同的git仓库时(gitLab/gitHub)时,除了全局的用户配置定义,我们可以为不同仓库自定义不同用户名和邮件 1.查询全局的配置:git config ...
- SpringCloud商品服务调用方式之feign
简介:改造电商项目 order-service服务 调用商品服务获取商品信息 Feign: 伪RPC客户端(本质还是用http) 官方文档: https://cloud.spring.io/sprin ...
- linux 常用命令(一)——查看硬盘空间-内存-线程的cpu负载-线程内存
系统参数检查: df -h [enter] 检查硬盘空间 TIP: 使用 man df 可查看该命令使用说明 ; q 退出. free检查内存使用情况: free [enter] TIP: 使用 ma ...
- webpack4 插件ProvidePlugin使用遇到的问题
根据博客https://www.cnblogs.com/geyouneihan/p/9769808.html学习webpack4中使用ProvidePlugin遇到了自定义js无法使用的问题,解决之后 ...
- go实现堆排序
package main import "fmt" func main(){ arr:=[]int{4,8,2,1,6,9,3,5,7,8,1,4} dui(arr) fmt.Pr ...
- ffplay 播放网络摄像头视频
shell脚本如下,无须加port ffplay rtsp://cameral_ip
- lsyncd替代inotify+rsync实现实时同步
因公司业务需要需要实时同步日志文件,刚一开始使用的是inotify+rsync来实现实时同步,但时间久而久之发现同步的速度越来越慢,往往延迟好几个小时.查了一下网上的inotify+rsync方案基本 ...
