NOIP初赛：完善程序做题技巧

最近写的文章好像还很多的。那么今天我们来讨论NOIP初赛的题型——完善程序。完善程序相对是比较难的题目了。全卷100分，完善程序占了大概26分，占比非常大。如果和英语考试试卷做比较，相当于首字母填空（估计是很多人的噩梦）。这类题型难度很大。本文讲一下做类似题目的方法。

不过首先，需要足够的知识储备，不然再多技巧也没用。

第一步：看提示，提示往往有很大的作用。

举例：NOIP2016第一题。

完善程序： **（读入整数）**请完善下面的程序，使得程序能够读入两个 int 范围内的整数， 并将这两个整数分别输出，每行一个。（第一、五空 2.5 分，其余 3 分）
输入的整数之间和前后只会出现空格或者回车。输入数据保证合法。

看题目我们知道，肯定不会太简单，会暗藏玄机在里面。本人第一次做题的时候第一反应是高精度。（不过题目已经说明在int范围了）实际上，我们根据题意，可以大致判断是快速读入相关的考察。关于快速读入，我之前写过一篇文章，可以看这里来参考一下。链接：

https://www.cnblogs.com/jisuanjizhishizatan/p/14977531.html

再看NOIP2007的。

完善程序:
（求字符的逆序）下面的程序的功能是输入若干行字符串，每输入一行，就按逆序输出该行，最后键入-1终止程序。请将程序补充完整。

这类题目好像很简单的水题。逆序输出，其实就是首尾做交换，到中间位置。设置i，j两个下标进行交换，循环条件i<=j。

第二步，分析算法。有的题目一下子想不出或者描述比较复杂的话，我们尝试分析算法。分析算法，根据题目描述或者根据残缺的代码进行分析。例如，NOIP2016:

本题采用二分法。对于区间[l, r]，我们取中间点 mid 并判断租用到自行 车的人数能否达到 mid。判断的过程是利用贪心算法实现的。

根据题目我们可以直接知道是二分和贪心。我们截取一段代码分析：

while (l <= r) {
        mid = (l + r) / 2;
        if(④){
            ans = mid;
            l = mid + 1;
        }else
            r = ⑤;
    }

if中肯定是对一个东西的判断。根据题意，判断的内容是租用自行车的人数能否达到mid。所以结果就是check(mid)。

第5空更加简单，上面l=mid+1，下面r就是mid-1。（对称性）

第三步，套用模版。如果一些题目，分析算法比较麻烦，我们可以套用一些题目的模版。

例如，NOIP2009放置国王。

完善程序：
(国王放置) 在n*m的棋盘上放置k个国王，要求k个国王互相不攻击，有多少种不同的放置方法。假设国王放置在第(x,y)格，国王的攻击的区域是:(x-1,y-1), (x-1,y),(x-1,y+1),(x,y-1),(x,y+1),(x+1,y-1),(x+1,y),(x+1,y+1)。读入三个数n,m,k，输出答案。题目利用回溯法求解。棋盘行标号为0~n-1，列标号为0~m-1。

看代码开头，知道是递归回溯法的模版。

CCF基础篇，这里我把对应的模版格式写下来了。

再例如，NOIP2008找第k大，直接二分模版。

完善程序：

(找第k大的数) 给定一个长度为1,000,000的无序正整数序列, 以及另一个数n (1<=n<=1000000), 然后以类似快速排序的方法找到序列中第n大的数（关于第n大的数：例如序列{1，2，3，4，5，6}中第3大的数是4）。

大概就是这个样子。

第四步，分析空的含义。

第一类：初始化。NOIP2009:

int main(){
    cin >> n;
    for (i=1;i<=n;i++)
        cin >> a[i];
    tmp=0;
    ans=0;
    len=0;
    beg= [    ①    ] ;

我们就看这段，很明显是初始化，beg=0直接完成。

第二类，直接调用函数。NOIP2007第一题:

while(【③】)
    {
        cin  >>  line;
        【④】;

第4空，是反转的，直接调用上面编写的reverse即可。

第三类，上下文推断。

NOIP2009第一题:

for (i=1;i<=n;i++){
        if (tmp+a[i]>ans){
            ans=tmp+a[i];
            len=i-beg;
        }
        else if ( [       ②        ] &&i-beg>len)
            len=i-beg;

下面比上面少了ans=tmp+a[i]，不需要赋值，并且根据后文推断出这一段并不是tmp+a[i]<ans的（如果是小于就要重置beg和tmp），因此这题填tmp+a[i]=ans。

NOIP2015打印日历：

for (i = 1; i <= ③; i++)
    {
        cout << ④;
        if (i == dayNum[m] || ⑤ == 0)
            cout << endl;
        else
            cout << '\t';
    }

我们知道，每次输出的是日期。输入月份，输出的应该依次1到daynum[m]作为日期。

什么情况需要换行？我们知道，7天换一次行，因此是i%7。

如果你这样想，就错了！！！在月初，有一些空格。（请注意1前面4个空格）

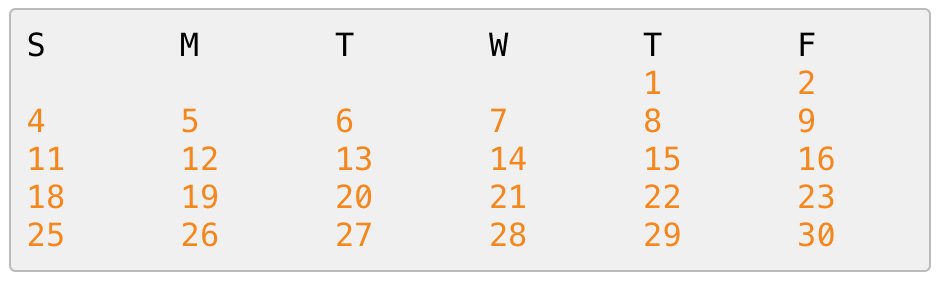
空格的数量记录在哪里呢？是记录在offset变量的。因此，是(offset+i)%7。

然后我们看NOIP2015中位数。

mid = (lbound + rbound) / 2;
        ②;
        for (i = 0; i < n; i++)
            if (③)
                ④;
        if (count > n / 2)
            lbound = mid + 1;
        else
            ⑤;

第二空是初始化类型，直接count=0。

第三空是上下文推断。下文有count，只有可能在这一语句里面出现count相关的东西。因此，推测第四空count++。

什么情况下count要++？这题求中位数，在之后要根据count的值在n的多少继续二分。我们假设，继续二分找中位数的区间在右边（从mid+1到rbound），说明count>n/2，一半以上的数小于中位数，刚好与count>n/2对应（一半以上的数小于count），因此这一空是x[i]>=mid。

第四类，对称性

也就是上面2015没有讲完的第五空，上面是mid+1，下面就是mid（注意此题比较特殊，不是mid-1，我就被坑过）很多二分的题目都是这样的。

全文完。