图论---DFS

图论---DFS

1. 图的遍历

在理解DFS算法之前，我们首先需要对什么是遍历进行了解，遍历的概念就是：从某一个点出发（一般是首或尾），依次将数据结构中的每一个数据访问且只访问一遍。

2. DFS简介

DFS（Depth-First-Search，深度优先搜索）算法的具体做法是：从某个点一直往深处走，走到不能往下走之后，就回退到上一步，直到找到解或把所有点走完。

在实现这一个依次的访问顺序时，操作动作存储与数据结构（栈）的思想及其相似，同时也由于栈的性质，我们可以通过递归来简化栈的创建，因此DFS算法的两种做法分别时利用栈或者递归实现。

算法步骤（递归或栈实现）

a)访问指定起始地点。

b)若当前访问顶点的邻接顶点有未被访问的顶点，就任选一个访问。如果没有就回退到最近访问的顶点，直到与起始顶点相通的所有点被遍历完。

c)若途中还有顶点未被访问，则再选一个点作为起始顶点，并重复前面的步骤。

3. 图的DFS

我们直接以案例进行讲解，就本图而言，其访问顺序可以是（不唯一）：1-2-4-5-3

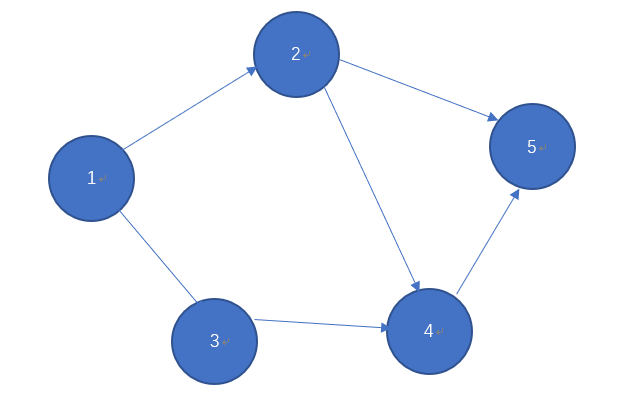
首先从1开始，1结点处可以访问2，3两个结点，那么按照我们自定义的优先顺序线访问2结点，此时，2结点有4，5两个结点访问，依旧按次序访问呢4结点，4结点可以访问5结点，5结点无法继续向下访问故结束访问，并回退4结点，4结点无法没有其他分支且自己已被访问故又退回2结点，2结点的两个分支4，5结点均已被访问，故再退回1结点，此时只有3结点未被访问，访问3结点，最终得到次序：1-2-4-5-3

4.相关代码

DFS算法的相关模板如下：

void dfs()//参数用来表示状态
{
    if(到达终点状态)
    {
        ...//根据需求添加
        return;
    }
    if(越界或者是不合法状态)
        return;
    if(特殊状态)//剪枝，去除一些不需要访问的场景，不一定i俺家
        return ;
    for(扩展方式)
    {
        if(扩展方式所达到状态合法)
        {
            修改操作;//根据题意来添加
            标记；
            dfs（）；
            (还原标记)；
            //是否还原标记根据题意
            //如果加上（还原标记）就是 回溯法
        }  

    }
}

5. 图的DFS代码：

#include<iostream>
using namespace std;
#define matrix_size 20
typedef struct {
    int weight;
}AdjMatrix[matrix_size][matrix_size];

struct MGraph{
    int vex[matrix_size];
    AdjMatrix arcs;
    int vexnum,arcnum;
};
bool visited[matrix_size];    

int LocateVex(MGraph *G ,int v){
    int i;
    for ( i = 0; i < G->vexnum; i++)
    {
        if (G->vex[i]==v)
        {
            break;
        }
    }
    if (i>G->vexnum)
    {
        cout<<"not such vertex"<<endl;
        return -1;
    }
    return i;
}
//构造无向图
void CreateDN(MGraph *G){
    cin>>G->vexnum>>G->arcnum;
    for (int i = 0; i < G->vexnum; i++)
    {
        cin>>G->vex[i];
    }
    for (int i=0; i<G->vexnum; i++) {
        for (int j=0; j<G->vexnum; j++) {
            G->arcs[i][j].weight=0;
        }
    }
    for (int i = 0; i < G->arcnum; i++)
    {
        int v1,v2;
        cin>>v1>>v2;
        int n=LocateVex(G,v1);
        int m=LocateVex(G,v2);
        if (m==-1||n==-1)
        {
            cout<<"not this vertex"<<endl;
            return ;
        }
        G->arcs[n][m].weight=1;
        G->arcs[m][n].weight=1;
    }
    return ;
}
//输出函数
void PrintGrapth(MGraph G)
{
    for (int i = 0; i < G.vexnum; i++)
    {
        for (int j = 0; j < G.vexnum; j++)
        {
            cout<<G.arcs[i][j].weight<<" ";
        }
        cout<<endl;
    }
}
void visitVex(MGraph G,int v){
    cout<<G.vex[v];
}
int FirstAdjVex(MGraph G,int v){
    for (int i = 0; i < G.vexnum; i++)
    {
        //查找与数组下标为v的顶点之间有边的顶点，返回它在数组中的下标
        if (G.arcs[v][i].weight)
        {
            return i;
        }
    }
    return -1;
}
int NextAdjVex(MGraph G,int v,int w)
{
    //从前一个访问位置w的下一个位置开始，查找之间有边的顶点
    for(int i = w+1; i<G.vexnum; i++){
        if(G.arcs[v][i].weight){
            return i;
        }
    }
    return -1;
}

void DFS(MGraph G,int v){
    visited[v]=true;
    visitVex(G,v);
    for (int w  = FirstAdjVex(G,v); w >0;  w= NextAdjVex(G,v,w))
    {
        if (!visited[w])
        {
            DFS(G,w);
        }
    }
}
//深度优先搜索
void DFSTraverse(MGraph G){//
    int v;
    //将用做标记的visit数组初始化为false
    for( v = 0; v < G.vexnum; ++v){
        visited[v] = false;
    }
    //对于每个标记为false的顶点调用深度优先搜索函数
    for( v = 0; v < G.vexnum; v++){
        //如果该顶点的标记位为false，则调用深度优先搜索函数
        if(!visited[v]){
            DFS( G, v);
        }
    }
}
int main() {
    MGraph G;//建立一个图的变量
    CreateDN(&G);//初始化图
    DFSTraverse(G);//深度优先搜索图
    return 0;
}