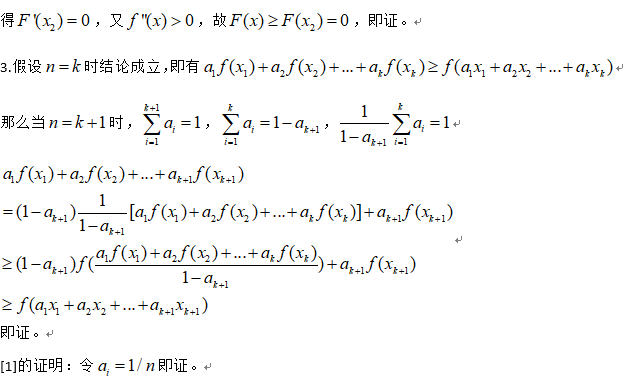
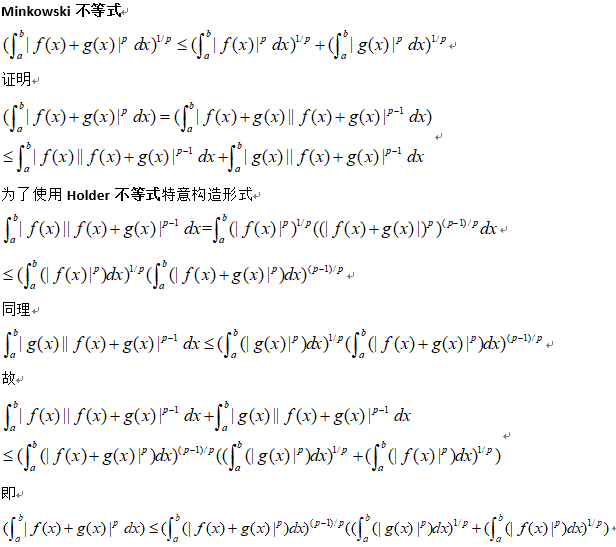
整理即证

参考资料：

[1].琴生不等式及其加权形式的证明.Balbooa.https://blog.csdn.net/balbooa/article/details/79357839.2018.2

[2].Minkowski不等式的证明. http://www.doc88.com/p-2542077482568.html

从Jensen不等式到Minkowski不等式的更多相关文章

  1. 如何理解Minkowski不等式

    [转载请注明出处]http://www.cnblogs.com/mashiqi 2017/02/16 Minkowski不等式: 设$f$是$\mathbb{R}^n \times \mathbb{R ...

  2. Markov不等式，Chebyshev不等式

    在切诺夫界的证明中用到了Markov不等式,证明于此~顺便把Chebyshev不等式也写上了

  3. Schur不等式（舒尔不等式）

    舒尔( Schur \texttt{Schur} Schur)不等式1 具体内容 Schur \texttt{Schur} Schur 不等式: x , y , z x,y,z x,y,z 为非负实数 ...

  4. 机器学习数学|微积分梯度jensen不等式

    机器学习中的数学 觉得有用的话,欢迎一起讨论相互学习~Follow Me 原创文章,如需转载请保留出处 本博客为七月在线邹博老师机器学习数学课程学习笔记 索引 微积分,梯度和Jensen不等式 Tay ...

  5. 《A First Course in Probability》-chaper8-极限定理-切比雪夫不等式

    基于对概率问题的抽象化,通过期望.方差.随机变量X及其概率,我们想要通过几个量推出另外几个量的特征,笼统的来说,极限定理起到的作用便在于此 切比雪夫不等式: 在证明切比雪夫不等式之前,我们先要完成对马 ...

  6. BZOJ 2762: [JLOI2011]不等式组( 平衡树 )

    对不等式变形..然后就是维护一些数, 随便找个数据结构都能写吧....用double感觉会有精度误差, 分类讨论把<改成<=了很久后弃疗了, 自己写了个分数体....然后速度就被完爆了.. ...

  7. bzoj 2762: [JLOI2011]不等式组——树状数组

    旺汪与旺喵最近在做一些不等式的练习.这些不等式都是形如ax+b>c 的一元不等式.当然,解这些不等式对旺汪来说太简单了,所以旺喵想挑战旺汪.旺喵给出一组一元不等式,并给出一个数值 .旺汪需要回答 ...

  8. 【BZOJ2762】[JLOI2011]不等式组 树状数组

    [BZOJ2762][JLOI2011]不等式组 Description 旺汪与旺喵最近在做一些不等式的练习.这些不等式都是形如ax+b>c 的一元不等式.当然,解这些不等式对旺汪来说太简单了, ...

  9. BZOJXXXX: [IOI2000]邮局——四边形不等式优化初探

    貌似$BZOJ$上并没有这个题... 是嫌这个题水了么... 还是要氪金权限号??? 这里附上洛谷的题面:洛谷P4767 [IOI2000]邮局 题目描述 高速公路旁边有一些村庄.高速公路表示为整数轴 ...

随机推荐

  1. loadrunner断言多结果返回

    有这么一个场景,接口返回的多个状态都是正常的,那么在压测的时候,断言就需要多 init里面执行登录,根据返回获取到tokenId action中,执行登录后的操作,获取响应返回的状态,把正确的状态个数 ...

  2. CMakeList.txt（3）： 一个cmake实例

    介绍一个比较实用的例子,即包含生成静态库又包含引入外部头文件和链接库的cmake demo. 先按照工程规范建立工程目录,并编写代码,以下面的工程目录为例进行解释这个例子,工程的目录结构为: 1. 编 ...

  3. windows下连接smb服务器

    在运行里面输入:\\xxx.xxx.xxx.xxx   即可访问远程服务器

  4. zeppelin中连接hive和impala

    连接Hive 新建interpreter default.driver = org.apache.hive.jdbc.HiveDriver default.url = jdbc:hive2://hos ...

  5. ModBus-RTU详解

      Modbus 一个工业上常用的通讯协议.一种通讯约定.Modbus协议包括RTU.ASCII.TCP.其中MODBUS-RTU最常用,比较简单,在单片机上很容易实现.虽然RTU比较简单,但是看协议 ...

  6. [面试]synchronized

    synchronized 把面试中遇到的问题进行了整理. 本篇文章copy+整理自: 1. http://www.cnblogs.com/lingepeiyong/archive/2012/10/30 ...

  7. 半导体知识：蚀刻（Etch）工艺讲解

    本文转载自微信公众号 - 半导体行业观察  , https://mp.weixin.qq.com/s/F3LXiub6n4iYsQDqDH9K_g

  8. [Reinforcement Learning] Model-Free Prediction

    上篇文章介绍了 Model-based 的通用方法--动态规划,本文内容介绍 Model-Free 情况下 Prediction 问题,即 "Estimate the value funct ...

  9. L1-Day5

    1.他偷了那个装满钱的书包. [我的翻译]He stole the bag full of money. [标准答案]He stole that school bag full of money. ( ...

  10. 利用request和re抓取猫眼电影排行

    import requests import re import time def get_one_page(url): headers = { 'User-Agent': 'Mozilla/5.0 ...