DeepCTR专题：DeepFM论文学习和实现及感悟

论文地址：https://arxiv.org/pdf/1703.04247.pdf

CTR预估我们知道在比较多的应用场景下都有使用。如：搜索排序、推荐系统等都有广泛的应用。并且CTR具有极其重要的 地位，特别相对广告推荐领域来说更加如此，竞价广告需要通过ctr给出相应的价格，并由此获得广告曝光的机会。而ctr的大小决定了出价的高低，直接会影响到该广告是否能得到曝光机会。这里涉及到计算广告相关的知识，暂时就不展开讲了。这里主要介绍一下DeepFM该算法的基本原理和网络框架。

论文总体来看还是相对比较容易的，主要分为三个部分：

第一部分：算法的主要背景

第二部分：DeepFM的基本网络框架和原理

第三部分：实验（papers必须有的部分）

下面分别从我个人理解的角度来说说每个部分吧：

1、DeepFM算法的背景

（1）首先我们同样要回顾一下FM算法的基本原理，FM主要是在LR的基础上增加了二阶交叉项的概念，从而可以获得一些轿车特征。但是算法每个特征两两交叉的话，算法复杂度是O(n平方)，

所以，为了优化FM算法，将矩阵分解应用其中。

　　FM的缺点是：

　　1）仅仅两两之间的交叉特征

　　2）只能获得二阶交叉的特征，对于高阶特征并没有涉及

（2）从16年wide-deep算法中，或多或少的作者受到了一些启发，于是想到可以对FM算法利用深度学习进行优化，预计就提出了DeepFM算法。

2、DeepFM算法的基本原理（个人觉得还是比较简单的）

（1）总体网络结构

　　　　　　　　　　　　　　　　

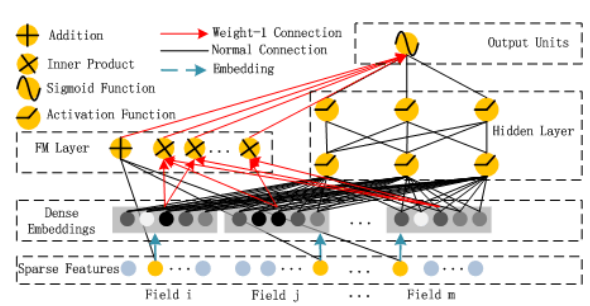
　　网络结构中，主要包含Deep部分和FM部分，网络结构类似Wide-Deep结构。

（2）算法的原理

　　首先网络最终输出是：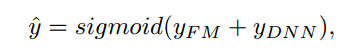

　　其中，FM部分如下所示：

　　　　　　　　　　

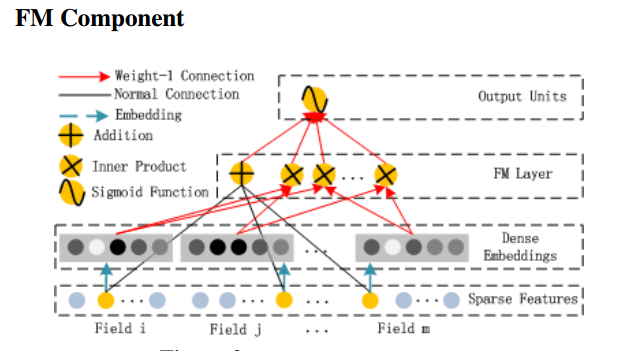
　　Deep部分如下所示：

　　　　　　　　　　

网络就是这么简单，就是讲这两部分的输出进行求和并输出。

3、实验。实验部分可以学习别人调节参数的经验。

（1）Dropout设置：

　　　　　　　　　　

　　从作者的实验来看，dropout设置为0.9效果最佳

（2）隐藏层数设定

　　　　

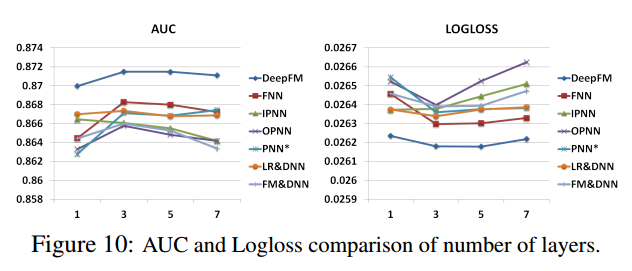
　　从上图来看，作者实验数据表明，隐层数量=3效果最佳

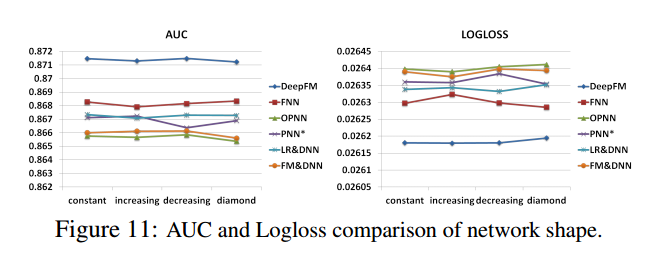
（3）隐藏层神经元个数

　　　　神经元个数的变化: constant (200-200-200), increasing (100-200-300),decreasing (300-200-100), and diamond (150-300-150)