UOJ#172. 【WC2016】论战捆竹竿 字符串 KMP 动态规划 单调队列 背包

原文链接https://www.cnblogs.com/zhouzhendong/p/UOJ172.html

题解

首先，这个问题显然是个背包问题。

然后，可以证明：一个字符串的 border 长度可以划分成 $O(log |S|)$ 个等差数列。

(以下图片摘自  金策 - 《字符串算法选讲》)

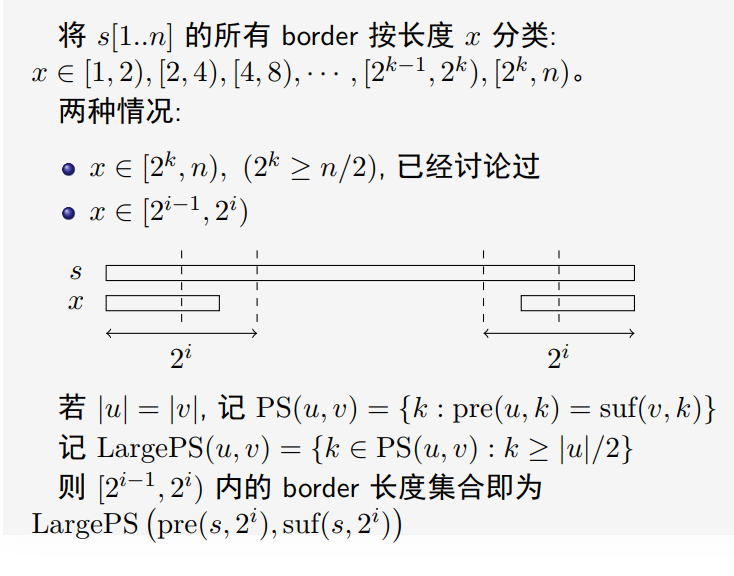
由于长度 n 可以随便取，所以我们可以在对n取模的意义下做背包，设 dis[i] 为 占用背包容量%n = i 时至少要占用多少背包容量，那么直接建 $n^2$ 条边跑一下 dijkstra 就可以在 $O(n^2\log n )$ 的时间复杂度内解决此题。

对于所有的长度，我们将其分组，保证每一组是一个等差数列。

我们枚举等差数列，依次将其加入背包。

假设最终背包中最多包含当前等差数列的一个元素，那么比较好做，直接单调队列就好了。

但是可以有多个当前等差数列的元素计入最终背包容量。也就是说，假设当前等差数列用 $v + kd$ 表示，那么可能会有 $tv + \sum k_i d$ 这种情况。这在对 n 取模的意义下非常难做。

于是我们考虑把它转化成对 $v$ 取模的意义下的结果，这样就方便多了。

考虑如何转化：先把原先在对 n 取模意义下的结果放到对 v 取模意义下的数组里，然后考虑每一个 $dis'[i]$ 都可以更新 $dis'[(i+n)\mod v ]$，即 $dis'[(i+n)\mod v] =min(dis'[(i+n)\mod v],dis'[i] + n)$ 。

把转移形成的环搞出来，dp转移一下就可以得到新的dis数组。

剩下的单调队列+dp也类似。

于是时间复杂度是 $O(n\log n)$ 。

代码

#pragma GCC optimize("Ofast","inline")
#include <bits/stdc++.h>
#define clr(x) memset(x,0,sizeof (x))
#define fi first
#define se second
using namespace std;
typedef long long LL;
LL read(){
	LL x=0,f=0;
	char ch=getchar();
	while (!isdigit(ch))
		f|=ch=='-',ch=getchar();
	while (isdigit(ch))
		x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return f?-x:x;
}
const int N=500005;
const LL INF=2e18;
int T,n,m;
LL w;
int Fail[N],nf[N];
struct brd{
	int v,d,c;
}b[N];
char s[N];
LL dis[N],rng;
LL gcd(LL a,LL b){
	return b?gcd(b,a%b):a;
}
void Trans(LL nr){
	static LL d[N];
	for (int i=0;i<nr;i++)
		d[i]=INF;
	for (int i=0;i<rng;i++)
		d[dis[i]%nr]=min(d[dis[i]%nr],dis[i]);
	int g=gcd(rng,nr);
	for (int t=0;t<g;t++){
		int e=nr/g*2,_i=t,rg=rng%nr;
		for (LL i=t,j=0;j<e;i+=rng,j++){
			d[_i]=min(d[_i],d[_i<rg?_i-rg+nr:_i-rg]+rng);
			if ((_i+=rg)>=nr)
				_i-=nr;
		}
	}
	rng=nr;
	for (int i=0;i<rng;i++)
		dis[i]=d[i];
}
pair <LL,LL> Q[N*2];
int head,tail;
void DP(int d,int c){
	int g=gcd(rng,d);
	for (int t=0;t<g;t++){
		head=1,tail=0;
		int e=rng/g*2,_i=t;
		for (LL i=t,j=0;j<e;i+=d,j++){
			if (head<=tail&&Q[head].fi+(LL)c*d<=i)
				head++;
			if (head<=tail)
				dis[_i]=min(dis[_i],Q[head].se+rng+i);
			while (head<=tail&&Q[tail].se>=dis[_i]-i)
				tail--;
			Q[++tail]=make_pair(i,dis[_i]-i);
			if ((_i+=d)>=rng)
				_i-=rng;
		}
	}
}
int main(){
	T=read();
	while (T--){
		n=read(),w=read();
		scanf("%s",s+1);
		Fail[1]=0;
		for (int i=2;i<=n;i++){
			int k=Fail[i-1];
			while (k>0&&s[k+1]!=s[i])
				k=Fail[k];
			if (s[k+1]==s[i])
				k++;
			Fail[i]=k;
		}
		m=0;
		for (int i=n;i>0;i=Fail[i])
			nf[Fail[i]]=i;
		for (int j=0;j<n;j=nf[j]){
			int i=n-j;
			if (j==0)
				m++,b[m].v=i,b[m].d=0,b[m].c=1;
			else if (!b[m].d)
				b[m].d=b[m].v-i,b[m].c++,b[m].v=i;
			else if (b[m].v-b[m].d==i)
				b[m].v=i,b[m].c++;
			else
				m++,b[m].v=i,b[m].d=0,b[m].c=1;
		}
		if (!b[m].d)
			b[m].d=1;
		clr(dis);
		rng=n;
		for (int i=0;i<n;i++)
			dis[i]=INF;
		dis[0]=n;
		for (int i=1;i<=m;i++){
			Trans(b[i].v);
			DP(b[i].d,b[i].c);
		}
		LL ans=0;
		for (int i=0;i<rng;i++)
			if (dis[i]<=w)
				ans+=w/rng-dis[i]/rng+(w%rng>=dis[i]%rng?1:0);
		cout<<ans<<endl;
	}
	return 0;
}