P1962 斐波那契数列

题面是这样的，其实斐波那契我们之前也有接触过，并不是什么太陌生的玩意，第一个想到的方法其实是用递归来做，这样的话其实是非常轻松的，but同志们你们有没有关注过这样一个鬼东西

你以为蓝题是让你切着玩的吗？？？？？？

果不其然，递归写了一个，大红大紫啊喂

（雾

不过的确过不了就是了，直到我打开了题解，发现了一个叫矩阵快速幂的玩意

Fn表示数列的第n项

那么我们如果把Fn，Fn-1写成蒟阵的形式，可以按照如下推导过程对这个蒟阵进行拆分，从而写成便于计算的形式

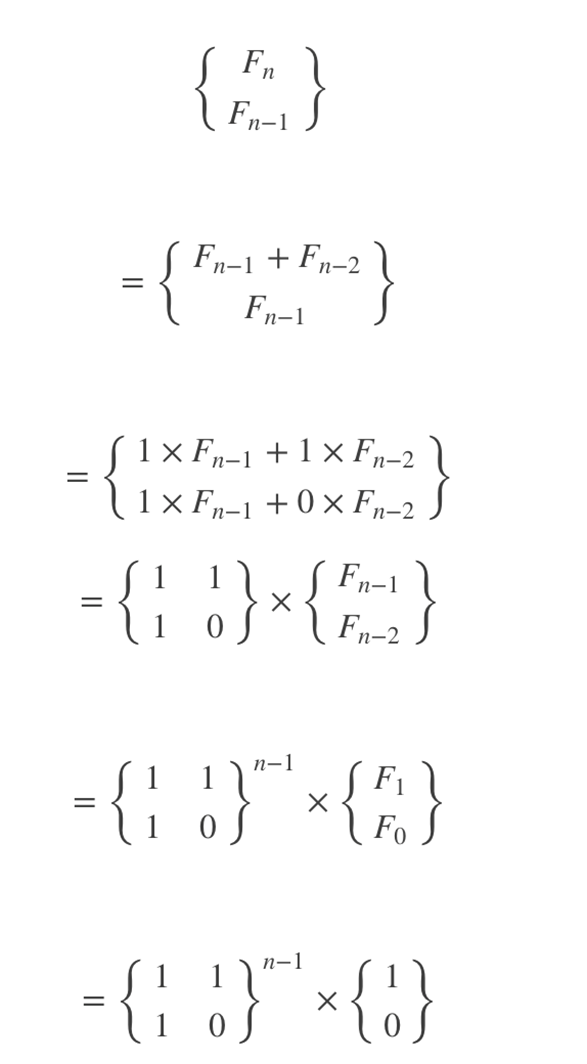
其实我们就是把递归用矩阵的方式写了出来，然后想求第n项就直接输出矩阵的n次幂即可

快速幂在另一篇博客里看这里qaq

其实这道题的难点就是矩阵快速幂，既然会了这个的话就没什么大问题啦~

代码如下：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int,int> pr;
const double pi=acos(-);
#define rep(i,a,n) for(ll i=a;i<=n;i++)
#define per(i,n,a) for(ll i=n;i>=a;i--)
#define Rep(i,u) for(int i=head[u];i;i=Next[i])
#define clr(a) memset(a,0,sizeof a)
#define pb push_back
#define mp make_pair
#define fi first
#define sc second
ld eps=1e-;
ll pp=;
ll mo(ll a,ll pp){if(a>= && a<pp)return a;a%=pp;if(a<)a+=pp;return a;}
ll powmod(ll a,ll b,ll pp){ll ans=;for(;b;b>>=,a=mo(a*a,pp))if(b&)ans=mo(ans*a,pp);return ans;}
ll read(){
    ll ans=;
    char last=' ',ch=getchar();
    while(ch<'' || ch>'')last=ch,ch=getchar();
    while(ch>='' && ch<='')ans=ans*+ch-'',ch=getchar();
    if(last=='-')ans=-ans;
    return ans;
}
//head   从这里开始哦
struct matrix{
    ll a[][];
};//注意这里要用ll保证不会爆
matrix operator *(matrix a, matrix b){//定义*运算
    matrix c;
    rep(i,,)//简写的方式，for（int i =1;i<=n;++i)        
　　 rep(j,,){
            c.a[i][j]=;
            rep(k,,)
                c.a[i][j] = (c.a[i][j]+a.a[i][k]*b.a[k][j])%pp;
        }
    return c;
}
ll k;
int main(){
    cin>>k;
    matrix a;
    a.a[][]=;a.a[][]=;
    a.a[][]=;a.a[][]=;
    matrix ans;
    ans.a[][]=;ans.a[][]=;
    ans.a[][]=;ans.a[][]=;//把ans初始化为单位矩阵
    ll b=k-;
    while(b){
        if(b&)ans=ans*a;
        a=a*a;
        b/=;
    }//一个快速幂
    ll fk = (ans.a[][]+ ans.a[][])%pp;
    cout<<fk<<endl;//O(log B *2^3)
}