MT【69】斯图姆定理
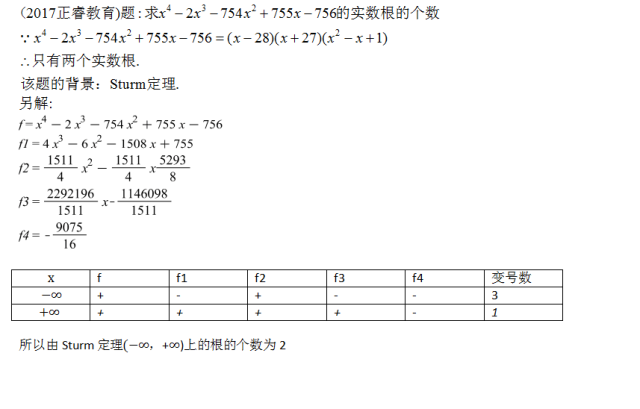
评:如果说零点存在定理是“只在此山中,云深不知处”的意境。那么斯图姆定理就能处理多项式的零点个数以及定位.
MT【69】斯图姆定理的更多相关文章
- 帕斯瓦尔定理(Parseval's theorem)
∫∞−∞|x(t)|2dt=12π∫∞−∞|X(ω)|2dω=∫∞−∞|X(2πf)|2df∑n=−∞∞|x[n]|2=12π∫π−π|X(eiϕ)|2dϕ∑n=0N−1|x[n]|2=1N∑k=0N ...
- 奈奎斯特采样定理(Nyquist)
采样定理在1928年由美国电信工程师H.奈奎斯特首先提出来的,因此称为奈奎斯特采样定理. 1933年由苏联工程师科捷利尼科夫首次用公式严格地表述这一定理,因此在苏联文献中称为科捷利尼科夫采样定理. 1 ...
- MT【144】托兰定理【图论】
平面上$2n$个点$(n>1,n\in N)$,无三点共线,任意两点连线段,将其中任意$n^2+1$条线段染红色. 求证:三边都为红色的三角形至少有$\left[\dfrac{2}{3}(n+\ ...
- poj 1659 判断是否能构成图Havel-Hakimi定理
//用到了Havel-Hakimi定理,判断是否能够构图 //两种情况不能构图,1:对剩下序列排序后,最大的度数超过了剩下的顶点数 // 2:对最大的度数后面的f个度数减-后,出现了负数 //记录到临 ...
- Havel-Hakimi定理---通过度数列判断是否可图化
0.可图:一个非负整数组成的序列如果是某个无向图的度序列,则该序列是可图的. 1.度序列:Sequence Degree,若把图G所有顶点的度数排成一个序列,责成该序列为图G的一个序列.该序列可以是非 ...
- LDA概率图模型之贝叶斯理解
贝叶斯.概率分布与机器学习 转自:http://www.cnblogs.com/LeftNotEasy/archive/2010/09/27/1837163.html 本文由LeftNotEasy原 ...
- HDU 2454"Degree Sequence of Graph G"(度序列可图性判断)
传送门 参考资料: [1]:图论-度序列可图性判断(Havel-Hakimi定理) •题意 给你 n 个非负整数列,判断这个序列是否为可简单图化的: •知识支持 握手定理:在任何无向图中,所有顶点的度 ...
- 世界城市 XML
下载地址:http://www.qlcoder.com/uploads/dd01140921/147988679320159.xml <Location> <CountryRegio ...
- Java程序员必备英文单词
列表中共有769个单词,这些单词是从JDK.Spring.SpringBoot.Mybatis的源码中解析得到,按照在源码中出现的频次依次排列,页面中的单词是出现频次大于1000的.单词的音标.翻译结 ...
随机推荐
- Redis详解(六)------ RDB 持久化
前面我们说过,Redis 相对于 Memcache 等其他的缓存产品,有一个比较明显的优势就是 Redis 不仅仅支持简单的key-value类型的数据,同时还提供list,set,zset,has ...
- 【webstorm】注册码 更新笔记
20190225 1.修改hosts文件,windows的hosts文件路径是 C:\ Windows \ System32 \ drivers \ etc \ hosts 0.0.0.0 acco ...
- ASP.NET RAZOR自动生成的js Timer
<input type="hidden" value="@(Model.TimeLength)" id="examTimeLength" ...
- java 基础02 打包package
- 非关系型数据库(nosql)介绍
非关系型数据库也叫Nosql数据库,全称是not noly sql. 2009年初,Johan Oskarsson举办了一场关于开源分布式数据库的讨论,Eric Evans在这次讨论中提出了NoSQL ...
- cmd命令入门
第一类: 介绍原生的DOS 首先在cmd命令输入help,看到如下图的结果,这里展示的原生的DOS命令. 这里列出了一些命令,可以自己试试的玩.一般看到一个命令后,如果没有说明文档,你就尝试的在其命令 ...
- 【精】【入门篇】js正则表达式
前言 最近有了点时间,就回头看了一下<学习正则表达式>这本书.怎么说呢,这本书适合从零开始学习正则表达式或者有一点基础但是想要加强这方面能力的读者.这本书的风格是“实践出真知”,使用归纳方 ...
- 关于Prometheus运维实践项目
关于Promethues运维实践项目 1. 什么是Prometheus运维实践项目 是什么 Prometheus,普罗米修斯,是古希腊神话中为人间带来火种的神. Prometheus运维实 ...
- JS冷门知识盘点
(+new Date() 是简略写法,得到毫秒 超过多行显示省略号 overflow : hidden; text-overflow: ellipsis; display: -webkit-box; ...
- 矩形A + B HDU2524
题意 给你n*m的棋盘问有多少个矩形 分析 先看只有一行或一列的情况有1+2+....+n个,因为矩形的类型有1个最小单位格子n个,2个最小单位格子n-1个,n个最小单位格子有一个 code #inc ...
