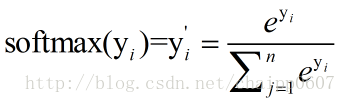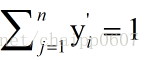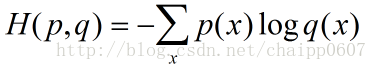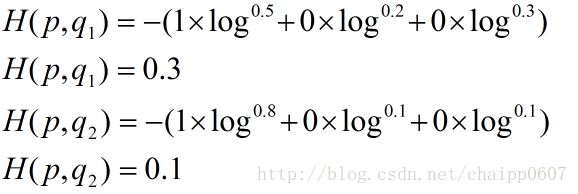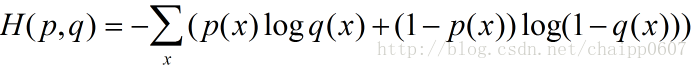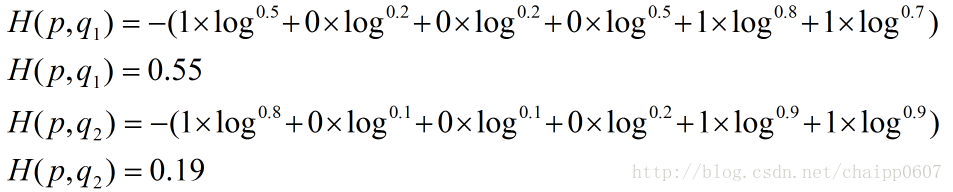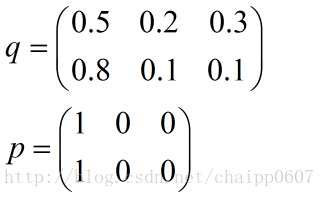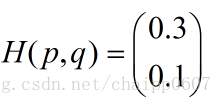理解交叉熵(cross_entropy)作为损失函数在神经网络中的作用
交叉熵的作用
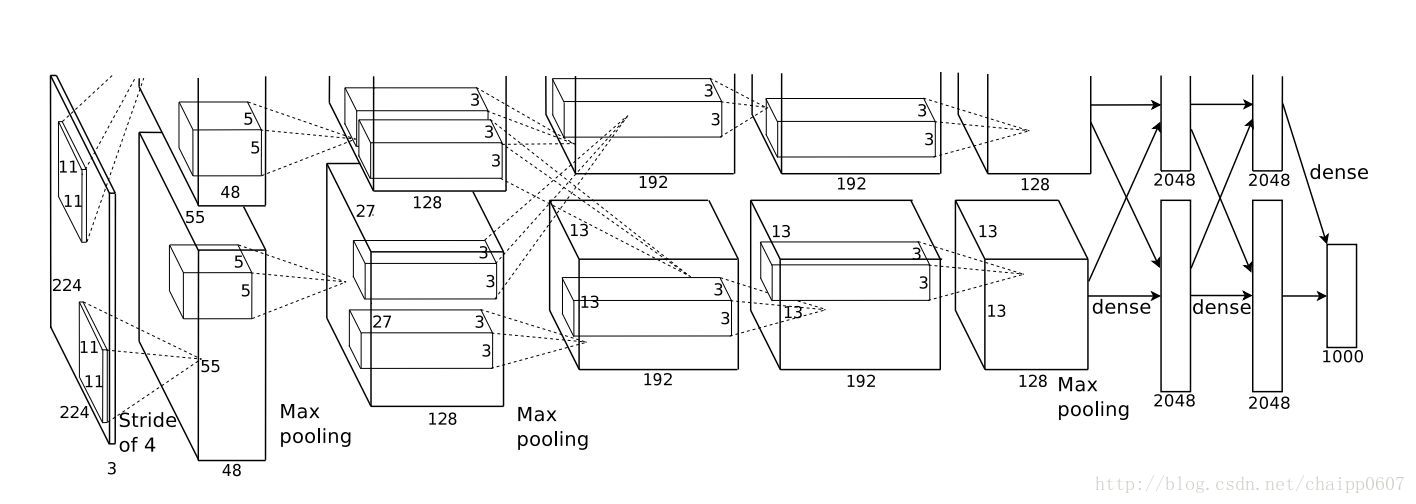
通过神经网络解决多分类问题时,最常用的一种方式就是在最后一层设置n个输出节点,无论在浅层神经网络还是在CNN中都是如此,比如,在AlexNet中最后的输出层有1000个节点:
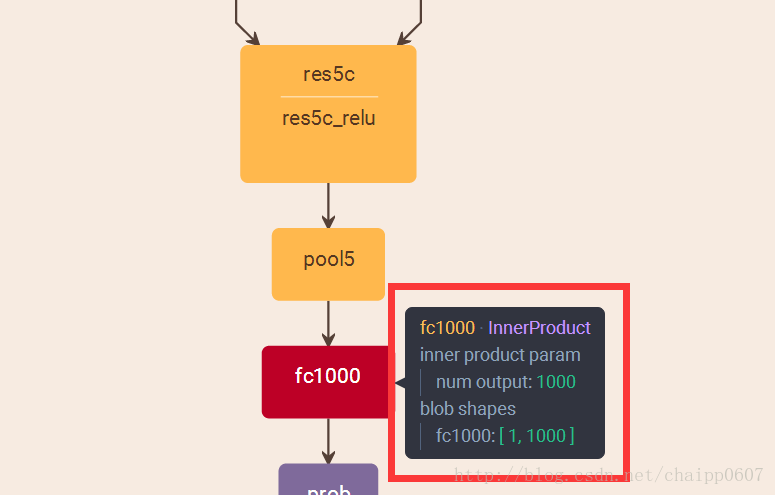
而即便是ResNet取消了全连接层,也会在最后有一个1000个节点的输出层:
一般情况下,最后一个输出层的节点个数与分类任务的目标数相等。假设最后的节点数为N,那么对于每一个样例,神经网络可以得到一个N维的数组作为输出结果,数组中每一个维度会对应一个类别。在最理想的情况下,如果一个样本属于k,那么这个类别所对应的的输出节点的输出值应该为1,而其他节点的输出都为0,即[0,0,1,0,….0,0],这个数组也就是样本的Label,是神经网络最期望的输出结果,交叉熵就是用来判定实际的输出与期望的输出的接近程度!
Softmax回归处理
神经网络的原始输出不是一个概率值,实质上只是输入的数值做了复杂的加权和与非线性处理之后的一个值而已,那么如何将这个输出变为概率分布?
这就是Softmax层的作用,假设神经网络的原始输出为y1,y2,….,yn,那么经过Softmax回归处理之后的输出为:
很显然的是:
而单个节点的输出变成的一个概率值,经过Softmax处理后结果作为神经网络最后的输出。
交叉熵的原理
交叉熵刻画的是实际输出(概率)与期望输出(概率)的距离,也就是交叉熵的值越小,两个概率分布就越接近。假设概率分布p为期望输出,概率分布q为实际输出,H(p,q)为交叉熵,则:
这个公式如何表征距离呢,举个例子:
假设N=3,期望输出为p=(1,0,0),实际输出q1=(0.5,0.2,0.3),q2=(0.8,0.1,0.1),那么:
很显然,q2与p更为接近,它的交叉熵也更小。
除此之外,交叉熵还有另一种表达形式,还是使用上面的假设条件:
其结果为:
以上的所有说明针对的都是单个样例的情况,而在实际的使用训练过程中,数据往往是组合成为一个batch来使用,所以对用的神经网络的输出应该是一个m*n的二维矩阵,其中m为batch的个数,n为分类数目,而对应的Label也是一个二维矩阵,还是拿上面的数据,组合成一个batch=2的矩阵:
所以交叉熵的结果应该是一个列向量(根据第一种方法):
而对于一个batch,最后取平均为0.2。
在TensorFlow中实现交叉熵
在TensorFlow可以采用这种形式:
cross_entropy = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0))) 其中y_表示期望的输出,y表示实际的输出(概率值),*为矩阵元素间相乘,而不是矩阵乘。
上述代码实现了第一种形式的交叉熵计算,需要说明的是,计算的过程其实和上面提到的公式有些区别,按照上面的步骤,平均交叉熵应该是先计算batch中每一个样本的交叉熵后取平均计算得到的,而利用tf.reduce_mean函数其实计算的是整个矩阵的平均值,这样做的结果会有差异,但是并不改变实际意义。
除了tf.reduce_mean函数,tf.clip_by_value函数是为了限制输出的大小,为了避免log0为负无穷的情况,将输出的值限定在(1e-10, 1.0)之间,其实1.0的限制是没有意义的,因为概率怎么会超过1呢。
由于在神经网络中,交叉熵常常与Sorfmax函数组合使用,所以TensorFlow对其进行了封装,即:
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(y_ ,y)
与第一个代码的区别在于,这里的y用神经网络最后一层的原始输出就好了。
转:http://blog.csdn.net/chaipp0607/article/details/73392175
理解交叉熵(cross_entropy)作为损失函数在神经网络中的作用的更多相关文章
- 最大似然估计 (Maximum Likelihood Estimation), 交叉熵 (Cross Entropy) 与深度神经网络
最近在看深度学习的"花书" (也就是Ian Goodfellow那本了),第五章机器学习基础部分的解释很精华,对比PRML少了很多复杂的推理,比较适合闲暇的时候翻开看看.今天准备写 ...
- 深度学习基础系列(五)| 深入理解交叉熵函数及其在tensorflow和keras中的实现
在统计学中,损失函数是一种衡量损失和错误(这种损失与“错误地”估计有关,如费用或者设备的损失)程度的函数.假设某样本的实际输出为a,而预计的输出为y,则y与a之间存在偏差,深度学习的目的即是通过不断地 ...
- 【转载】深度学习中softmax交叉熵损失函数的理解
深度学习中softmax交叉熵损失函数的理解 2018-08-11 23:49:43 lilong117194 阅读数 5198更多 分类专栏: Deep learning 版权声明:本文为博主原 ...
- softmax交叉熵损失函数求导
来源:https://www.jianshu.com/p/c02a1fbffad6 简单易懂的softmax交叉熵损失函数求导 来写一个softmax求导的推导过程,不仅可以给自己理清思路,还可以造福 ...
- 交叉熵理解:softmax_cross_entropy,binary_cross_entropy,sigmoid_cross_entropy简介
cross entropy 交叉熵的概念网上一大堆了,具体问度娘,这里主要介绍深度学习中,使用交叉熵作为类别分类. 1.二元交叉熵 binary_cross_entropy 我们通常见的交叉熵是二元交 ...
- TensorFlow笔记-06-神经网络优化-损失函数,自定义损失函数,交叉熵
TensorFlow笔记-06-神经网络优化-损失函数,自定义损失函数,交叉熵 神经元模型:用数学公式比表示为:f(Σi xi*wi + b), f为激活函数 神经网络 是以神经元为基本单位构成的 激 ...
- 【机器学习基础】交叉熵(cross entropy)损失函数是凸函数吗?
之所以会有这个问题,是因为在学习 logistic regression 时,<统计机器学习>一书说它的负对数似然函数是凸函数,而 logistic regression 的负对数似然函数 ...
- 深度学习中交叉熵和KL散度和最大似然估计之间的关系
机器学习的面试题中经常会被问到交叉熵(cross entropy)和最大似然估计(MLE)或者KL散度有什么关系,查了一些资料发现优化这3个东西其实是等价的. 熵和交叉熵 提到交叉熵就需要了解下信息论 ...
- 交叉熵代价函数——当我们用sigmoid函数作为神经元的激活函数时,最好使用交叉熵代价函数来替代方差代价函数,以避免训练过程太慢
交叉熵代价函数 machine learning算法中用得很多的交叉熵代价函数. 1.从方差代价函数说起 代价函数经常用方差代价函数(即采用均方误差MSE),比如对于一个神经元(单输入单输出,sigm ...
随机推荐
- mysql 数据库设计
数据库设计 需求分析 *1.用户模块 用于记录记录注册用户信息 包括属性:用户名,密码,电话,邮箱,身份证号,地址,姓名,昵称... 可选唯一标志属性:用户名,电话,身份证号 存储特点:随系统上线时间 ...
- 描述符__get__,__set__,__delete__
描述符__get__,__set__,__delete__ # 描述符:1用来代理另外一个类的属性 # __get__():调用一个属性时,触发 # __set__():为一个属性赋值时触发 # __ ...
- boost asio 学习(六) 定时器
http://www.gamedev.net/blog/950/entry-2249317-a-guide-to-getting- started-with-boostasio?pg=7 6 定时器 ...
- PHP-自定义数组-预定义数组-自定义函数-预定义函数
(1)自定义数组 —— 项目中的重点 (2)PHP预定义数组 —— 重点&难点 (3)自定义函数 —— 了解 (4)PHP预定义函数 —— 项目中的重点 1.自定义数组 数组:array,一个 ...
- Unity AssetBundle打包资源工具
using UnityEngine;using System.Collections;using UnityEditor; /// <summary>/// 简单资源打包Editor/// ...
- tomcat是否有必要配置环境变量(摘)
之前发表了一篇关于如何安装和配置Tomcat的文章,而最近在开发项目的时候总是报错.后来被公司的大神问了一句:是谁告诉你Tomcat是需要配置环境变量的? 作为新手的我瞬间整个人都不好了!于是偷偷百度 ...
- PowerShell工作流学习-1-嵌套工作流和嵌套函数
关键点: a)嵌套深度没有任何语法限制,但是嵌套三个层次的工作流不支持任何通用参数,包括工作流通用参数 b)嵌套工作流可以调用当前范围和任何父范围内的工作流和函数 c)工作流不允许递归调用,脚本和函数 ...
- [转]kaldi中的在线识别----Online Recognizers
转自: http://blog.csdn.net/wbgxx333/article/details/24932533 本文是kaldi学习联盟中@冒顿翻译的,下面是@冒顿的翻译结果,在这里感谢@冒顿的 ...
- 拷问传统企业CIO:微服务化值得吗?
所谓数字化转型升级,就是以数字技术优化传统资源,企业需要谨慎地选择合适的技术逐步完成自己的数字化战略.以推出轻舟微服务平台的网易云为代表,云计算公司正在微服务领域发力,促进企业数字化创新.那么,微服务 ...
- ElasticSearch5.0之后的改变
ES5的变化 search_type=count和scan都移除了 count可以用size=0代替 GET /my_index/_search { "size": 0, &quo ...