Hanlp中N最短路径分词详细介绍

N-最短路径 是中科院分词工具NLPIR进行分词用到的一个重要算法，张华平、刘群老师在论文《基于N-最短路径方法的中文词语粗分模型》中做了比较详细的介绍。该算法算法基本思想很简单，就是给定一待处理字串，根据词典，找出词典中所有可能的词，构造出字串的一个有向无环图，算出从开始到结束所有路径中最短的前N条路径。因为允许相等长度的路径并列，故最终的结果集合会大于或等于N。

根据算法思想，当我们拿到一个字串后，首先构造图，接着针对图计算最短路径。下面以一个例子“他说的确实在理”进行说明，开始为了能够简单说明，首先假设图上的边权值均为1。

先给出对这句话的3-最短路(即路径最短的前3名, 因为有并列成分, 所以可能候选路径大于3)径求解过程图：

从节点4开始, 因为4是第一个出现多个前驱节点的

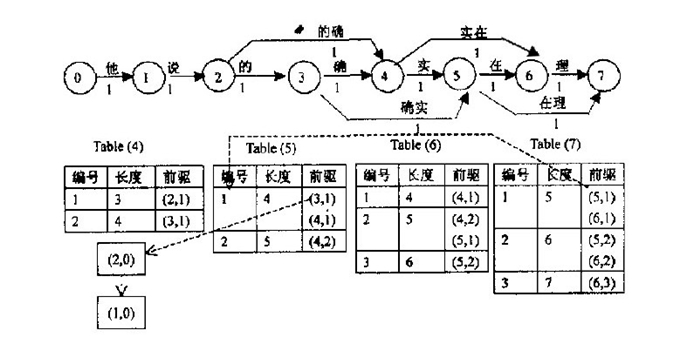
首先看图中上方，它是根据一个已有词典构造出的有向无环图。它将字串分为单个的字，每个字用图中相邻的两个结点表示，故对于长度为n的字串，需要n+1个结点。两节点间若有边，则表示两节点间所包含的所有结点构成的词，如图中结点2、3、4构成词“的确”。

图构造出来后，接下来就要计算最短路径，N-最短路径是基于Dijkstra算法的一种简单扩展，它在每个结点处记录了N个最短路径值与该结点的前驱，具体过程如上图中下方列表。Table(4)表示位于结点4时的最短路径情况，表示从结点0到4有两条路径，长度为3的路径前驱为2；长度为4的路径前驱为3。前驱括号里面第二个数表示对相同前驱结点的区分，如（4,1）、（4,2）。由列表可知，该字串的3-最短路径结果集合为｛5,5,6,6,7｝。

当然，在实际情况中，权值不可能都设为1的，否则随着字串长度n和最短路径N的增大，长度相同的路径数将会急剧增加。为了解决这样的问题，我们需要通过某种策略为有向图的边赋权重，很自然的想法就是边的权重就是该词出现的可能性。

NShortPath的基本思想是Dijkstra算法的变种，拿1-最短路来说吧，先Dijkstra求一次最短路，然后沿着最短路的路径走下去，只不过在走到某个节点的时候，检查到该节点在路径上的下一个节点是否还有别的路到它（从PreNode查），如果有，就走这些别的路中的没走过第一条（它们都是最短路上的途径节点）。然后推广到N-最短路，N-最短路中PreNode有N个，分别对应n-最短路时候的PreNode，就这么简单。

图解

再谈PreNode的准备

需要为每个顶点维护一个最小堆，最小堆里储存的是边的花费，每条边的终点是这个顶点。还需要维护到每个顶点的前N个最小路径的花费：

回忆一下Dijkstra求最短路的时候，我们只需记录一个最短路的累计花费就行了

这与此处的N-最短路径显著不同。

在遍历图的时候，与Dijkstra最短路径不同，N-最短路径从第二个节点开始，需要将当前节点可能到达的边根据累积第i短长度+该边的长度之和排序记录到PreNode队列数组中，排序由CQueue完成的。

然后从CQueue出队，这样路径长度就是升序了，按顺序更新 weightArray[当前节点][第几短路]就行了。

另外CQueue是一个不同于普通队列的队列，它维护了一个当前指针（下图的蓝色部分），这个蓝色指针在求解第i短路径的时候会用到。

假定看到这里，算法已经计算出了正确的PreNode队列，下面讨论如何从PreNode中找出N最短路径的确切途经节点集合。

1-最短路径的求解

整个计算过程维护了一个路径栈，对于上图来说，

1）首先将最后一个元素压入栈（本例中是6号结点），什么时候这个元素弹出栈，什么时候整个任务结束。

2）对于每个结点的PreNode队列，维护了一个当前指针，初始状态都指向PreNode队列中第一个元素。这个指针是由CQueue维护的，严格来讲不属于算法关心的问题。

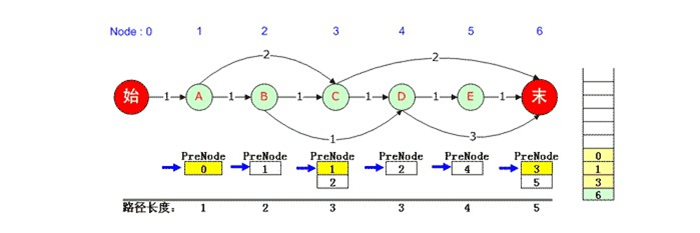
3）从右向左依次取出PreNode队列中的当前元素（当前元素出队）并压入栈，并将队列指针重新指向队列中第一个元素。如上图：6号元素PreNode是3，3号元素PreNode是1，1号元素PreNode是0。

4）当第一个元素压入栈后，输出栈内容即为一条队列。本例中0, 1, 3, 6便是一条最短路径。

5）将栈中的内容依次弹出，每弹出一个元素，就将当时压栈时该元素对应的PreNode队列指针下移一格。如果到了末尾无法下移，则继续执行第5步（也就是继续出栈），如果仍然可以移动，则执行第3步。

对于本例，先将“0”弹出栈，在路径上0的下一个是1，得出该元素对应的是1号“A”结点的PreNode队列，该队列的当前指针已经无法下移，因此继续弹出栈中的“1” ；同理该元素对应3号“C”结点，因此将3号“C”结点对应的PreNode队列指针下移。由于可以移动，因此将队列中的2压入队列，2号“B”结点的PreNode是1，因此再压入1，依次类推，直到0被压入，此时又得到了一条最短路径，那就是0，1，2，3，6。如下图：

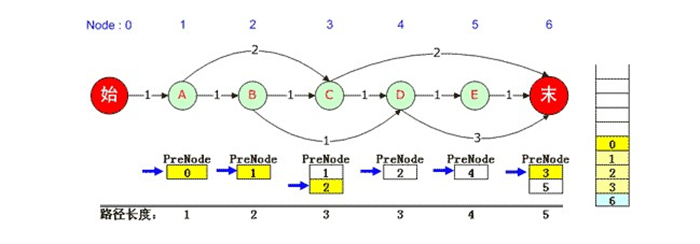
再往下，0、1、2都被弹出栈，3被弹出栈后，由于它对应的6号元素PreNode队列记录指针仍然可以下移，因此将5压入堆栈并依次将其PreNode入栈，直到0被入栈。此时输出第3条最短路径：0, 1, 2, 4, 5, 6。如下图：

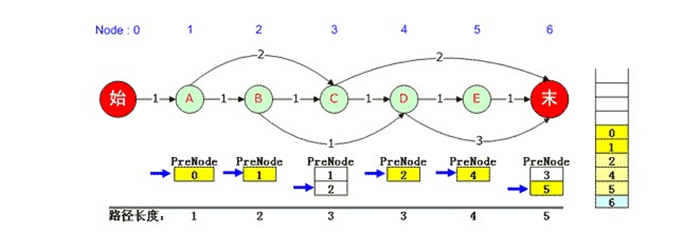
输出完成后，紧接着又是出栈，此时已经没有任何栈元素对应的PreNode队列指针可以下移，于是堆栈中的最后一个元素6也被弹出栈，此时输出工作完全结束。我们得到了3条最短路径，分别是：

0, 1, 3, 6,

0, 1, 2, 3, 6,

0, 1, 2, 4, 5, 6,

推广到N-最短路

N-最短路中PreNode有N个，分别对应n-最短路时候的PreNode，也就是当前路径是第n短的时候，当前节点对应的PreNode队列。

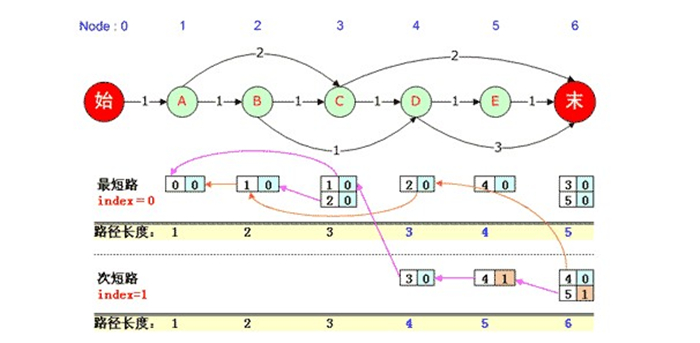
在该图中，观察黄颜色的路径长度表格，到达1号、2号、3号结点的路径虽然有多条，但长度只有一种长度，但到达4号“D”结点的路径长度有两种，即长度可能是3也可能是4，此时在“最短路”处（index＝0）记录长度为3时的PreNode，在“次短路”处（index＝1）处记录长度为4时的PreNode，依此类推。

值得注意的是，此时用来记录PreNode的坐标已经由前文求“1-最短路径”时的一个数（ParentNode值)变为2个数（ParentNode值以及index值）。

如上图所示，到达6号“末”结点的次短路径有两个ParentNode，一个是index=0中的4号结点，一个是index=1的5号结点，它们都使得总路径长度为6。

当N=2时，我们求得了2-最短路径，路径长度有两种，分别长度为5和6，而路径总共有6条，如下：

最短路径：

0, 1, 3, 6,

0, 1, 2, 3, 6,

0, 1, 2, 4, 5, 6,

========================

次短路径

0, 1, 2, 4, 6,

0, 1, 3, 4, 5, 6,

0, 1, 2, 3, 4, 5, 6,

---------------------