codeforces 916E Jamie and Tree dfs序列化+线段树+LCA

E. Jamie and Tree

time limit per test

2.5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

To your surprise, Jamie is the final boss! Ehehehe.

Jamie has given you a tree with n vertices, numbered from 1 to n. Initially, the root of the tree is the vertex with number 1. Also, each vertex has a value on it.

Jamie also gives you three types of queries on the tree:

1 v — Change the tree's root to vertex with number v.

2 u v x — For each vertex in the subtree of smallest size that contains u and v, add x to its value.

3 v — Find sum of values of vertices in the subtree of vertex with number v.

A subtree of vertex v is a set of vertices such that v lies on shortest path from this vertex to root of the tree. Pay attention that subtree of a vertex can change after changing the tree's root.

Show your strength in programming to Jamie by performing the queries accurately!

Input

The first line of input contains two space-separated integers n and q (1 ≤ n ≤ 105, 1 ≤ q ≤ 105) — the number of vertices in the tree and the number of queries to process respectively.

The second line contains n space-separated integers a1, a2, ..., an ( - 108 ≤ ai ≤ 108) — initial values of the vertices.

Next n - 1 lines contains two space-separated integers ui, vi (1 ≤ ui, vi ≤ n) describing edge between vertices ui and vi in the tree.

The following q lines describe the queries.

Each query has one of following formats depending on its type:

1 v (1 ≤ v ≤ n) for queries of the first type.

2 u v x (1 ≤ u, v ≤ n,  - 108 ≤ x ≤ 108) for queries of the second type.

3 v (1 ≤ v ≤ n) for queries of the third type.

All numbers in queries' descriptions are integers.

The queries must be carried out in the given order. It is guaranteed that the tree is valid.

Output

For each query of the third type, output the required answer. It is guaranteed that at least one query of the third type is given by Jamie.

Examples

input

6 7
1 4 2 8 5 7
1 2
3 1
4 3
4 5
3 6
3 1
2 4 6 3
3 4
1 6
2 2 4 -5
1 4
3 3

output

27
19
5

input

4 6
4 3 5 6
1 2
2 3
3 4
3 1
1 3
2 2 4 3
1 1
2 2 4 -3
3 1

output

18
21

Note

The following picture shows how the tree varies after the queries in the first sample.

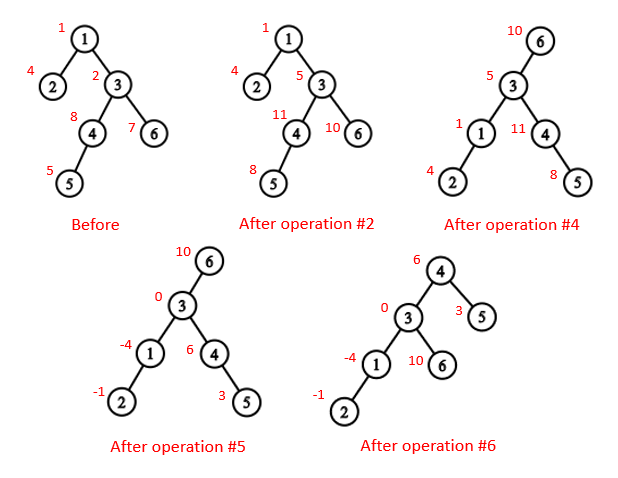
大意：给出一颗树，初始根节点为1，三种操作：

1.把一个节点变成根节点

2.给出两个节点u,v，把包含这两个点的最小子树中每个节点权值加上x

3.查询以 u 为根的子树的权值和。

题解：

如果没有操作一，这题就是把LCA和dfs序列化以及线段树的板子放在一起。

但是，对于操作一，如何解决？

其实并不需要真的把节点提到根上。

我们可以一直以 1 为根节点，利用一些小结论来进行2和3操作。

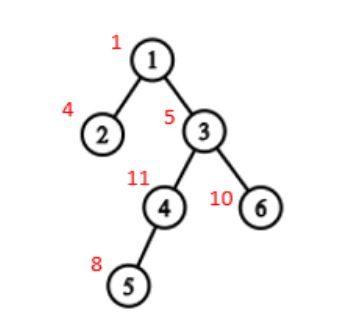
假设在该图中，当前根节点为6，但是我们的dfs序列仍然是以1为根节点的。

如果当前根节点不在要修改（查询）的子树中，就没有任何影响，直接修改（查询）即可，此处不做讨论。

下面只说根节点在要修改（查询）的子树中的情况。

如果现在给出操作2，把包含2,4的最小子树上面的每个节点加delta。

我们应该处理的节点是 1 2 3 4 5

lca(2,4)=1     lca(2,6)=1    lca(4,6)=3

有一个大胆的猜想：

直接修改lca(2,4)=1的子树，然后把不该修改的哪部分改回去。

那么多修改的哪部分是那些呢：

大胆猜想：

取这三组lca中深度最大的那个(节点3)

当前的根节点6所在的     节点3的子树     就是多修改的那部分。

对于询问操作，思想大体相似

若当前根节点为6，询问1的子树的权值和。

先算上整颗树，然后减去多加的部分。

多加的部分就是根节点6所在的     节点1的子树，也就是3，4，5，6。

大胆猜想，不用证明，恩，这结论就是对的。

 /*
 Welcome Hacking
 Wish You High Rating
 */
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<ctime>
 #include<cstdlib>
 #include<algorithm>
 #include<cmath>
 #include<string>
 using namespace std;
 int read(){
     int xx=,ff=;char ch=getchar();
     while(ch>''||ch<''){if(ch=='-')ff=-;ch=getchar();}
     while(ch>=''&&ch<=''){xx=(xx<<)+(xx<<)+ch-'';ch=getchar();}
     return xx*ff;
 }
 const int maxn=;
 int N,Q,opt,t1,t2,t3,root,v[maxn];
 int tid[maxn],rk[maxn],tim,Prev[maxn],depth[maxn],end[maxn];
 int lin[maxn],len;
 struct edge{
     int y,next;
 }e[maxn<<];
 inline void insert(int xx,int yy){
     e[++len].next=lin[xx];
     lin[xx]=len;
     e[len].y=yy;
 }
 void dfs(int x,int prev){
     depth[x]=depth[prev]+;
     tid[x]=++tim;
     rk[tim]=x;
     Prev[x]=prev;
     for(int i=lin[x];i;i=e[i].next)
         if(e[i].y!=prev)
             dfs(e[i].y,x);
     end[x]=tim;
 }
 int f[][maxn];
 int LCA(int x,int y){
     if(depth[x]<depth[y])
         swap(x,y);
     int dif=depth[x]-depth[y];
     for(int i=;i>=;i--)
         if(dif&(<<i))
             x=f[i][x];
     if(x==y)
         return x;
     for(int i=;i>=;i--)
         if(f[i][x]!=f[i][y])
             x=f[i][x],y=f[i][y];
     return f[][x];
 }
 int LCALCA(int x,int y){
     int t1=LCA(x,y),t2=LCA(x,root),t3=LCA(y,root);
     if(depth[t1]<depth[t2])
         swap(t1,t2);
     if(depth[t1]<depth[t3])
         return t3;
     return t1;
 }
 int get_son(int x){
     int temp=root;
     int dif=depth[root]-depth[x]-;
     for(int i=;i>=;i--)
         if(dif&(<<i))
             temp=f[i][temp];
     return temp;
 }
 struct Segment_Tree{
     long long sum,tag;
 }T[maxn<<];
 int X,Y,Z;
 void build(int L,int R,int root){
     if(L==R){
         T[root].sum=v[rk[L]];
         return;
     }
     int mid=(L+R)>>;
     build(L,mid,root<<);
     build(mid+,R,root<<|);
     T[root].sum=T[root<<].sum+T[root<<|].sum;
 }
 void upd(int L,int R,int root){
     if(X>R||Y<L)
         return;
     if(X<=L&&Y>=R){
         T[root].tag+=Z;
         T[root].sum+=1LL*(R-L+)*Z;
         return;
     }
     int mid=(L+R)>>;
     if(T[root].tag){
         T[root<<].tag+=T[root].tag;
         T[root<<|].tag+=T[root].tag;
         T[root<<].sum+=T[root].tag*(mid-L+);
         T[root<<|].sum+=T[root].tag*(R-mid);
         T[root].tag=;
     }
     upd(L,mid,root<<);
     upd(mid+,R,root<<|);
     T[root].sum=T[root<<].sum+T[root<<|].sum;
 }
 long long query(int L,int R,int root){
     if(X>R||Y<L)
         return ;
     if(X<=L&&Y>=R)
         return T[root].sum;
     int mid=(L+R)>>;
     if(T[root].tag){
         T[root<<].tag+=T[root].tag;
         T[root<<|].tag+=T[root].tag;
         T[root<<].sum+=T[root].tag*(mid-L+);
         T[root<<|].sum+=T[root].tag*(R-mid);
         T[root].tag=;
     }
     return query(L,mid,root<<)+query(mid+,R,root<<|);
 }
 int main(){
     //freopen("in.txt","r",stdin);
     N=read(),Q=read();root=;
     for(int i=;i<=N;i++)
         v[i]=read();
     for(int i=;i<N;i++){
         t1=read(),t2=read();
         insert(t1,t2);
         insert(t2,t1);
     }
     dfs(,);
     /*for(int i=1;i<=N;i++)
         printf("%d ",tid[i]);
     puts("");
     for(int i=1;i<=N;i++)
         printf("%d ",rk[i]);
     puts("");
     for(int i=1;i<=N;i++)
         printf("%d ",depth[i]);
     puts("");*/
     build(,N,);
     for(int i=;i<=N;i++)
         f[][i]=Prev[i];
     for(int i=;i<=;i++)
         for(int j=;j<=N;j++)
             f[i][j]=f[i-][f[i-][j]];
     while(Q--){
         opt=read();
         if(opt==)
             root=read();
         else if(opt==){
             t1=read(),t2=read(),t3=read();
             int lca=LCALCA(t1,t2);
             if(tid[root]>=tid[lca]&&tid[root]<=end[lca]){
                 X=,Y=N,Z=t3;
                 upd(,N,);
                 if(lca==root)
                     continue;
                 int temp=get_son(lca);
                 X=tid[temp],Y=end[temp],Z=-t3;
                 upd(,N,);
             }
             else{
                 X=tid[lca],Y=end[lca],Z=t3;
                 upd(,N,);
             }
         }
         else{
             int lca=read();
             if(lca==root){
                 X=,Y=N;
                 printf("%I64d\n",query(,N,));
             }
             else if(tid[root]>=tid[lca]&&tid[root]<=end[lca]){
                 long long ans=;
                 X=,Y=N;
                 ans=query(,N,);
                 int temp=get_son(lca);
                 X=tid[temp],Y=end[temp];
                 ans-=query(,N,);
                 printf("%I64d\n",ans);
             }
             else{
                 X=tid[lca],Y=end[lca];
                 printf("%I64d\n",query(,N,));
             }
         }
     }
     return ;
 }