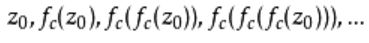OpenCV绘制朱利亚(Julia)集合图形
朱利亚集合是一个在复平面上形成分形的点的集合。以法国数学家加斯顿·朱利亚(Gaston Julia)的名字命名。
朱利亚集合可以由下式进行反复迭代得到:
对于固定的复数c,取某一z值(如z = z0),可以得到序列
这一序列可能反散于无穷大或始终处于某一范围之内并收敛于某一值。我们将使其不扩散的z值的集合称为朱利亚集合。
以下使用OpenCV编码绘制Julia集图形:
#include <Windows.h>
#include<highgui/highgui.hpp>
using namespace cv;
const int icount = 200; //迭代次数
const float c = -0.85; //实部
const float d = 0.088; //虚部
double m_real, m_image; //Mandelbro集
class ComplexClass
{
public:
double real;
double image;
ComplexClass(double r = 0, double i = 0) { real = r, image = i; }
};
ComplexClass operator+(const ComplexClass& a, const ComplexClass &b)
{
ComplexClass c;
c.real = a.real + b.real;
c.image = a.image + b.image;
return c;
}
ComplexClass operator*(const ComplexClass& a, const ComplexClass &b)
{
ComplexClass c;
c.real = a.real * b.real - a.image * b.image;
c.image = a.image * b.real + a.real * b.image;
return c;
}
double Model(ComplexClass a)
{
return sqrtf(a.real * a.real + a.image * a.image);
}
double Iteration(ComplexClass a, int n)
{
if (n == 0)
return Model(a);
else
{
ComplexClass temp = a*a;
temp.real += c;
temp.image += d;
// temp.real += m_real; 把这两句代替前面的两句就是mandelbrot集了
// temp.image += m_image;
return Iteration(temp, n - 1);
}
}
Vec3b dye(double dist)
{
if (dist < 1000000 && dist>-1000000)
return Vec3b(255, 0, 0);
else
return Vec3b(0, 0, 0); //Julia集之外的区域置为黑色
}
int main()
{
Mat image = Mat(Size(500, 500), CV_8UC3, Scalar::all(10));
for (int Y = 0; Y < image.rows; Y++)
{
for (int X = 0; X < image.cols; X++)
{
float x = (X - image.cols / 2) / 200.0;
float y = (Y - image.rows / 2) / 200.0;
m_real = x;
m_image = y;
ComplexClass a(x, y);
float dist = Iteration(a, icount);
image.at<Vec3b>(Y, X) = dye(dist);
}
}
//namedWindow("OpenCV For Julia", 0);
imshow("OpenCV For Julia | c = -0.85 d = 0.088", image);
waitKey();
}改变实部c和虚数b的值可以得到不同的图形,很漂亮。
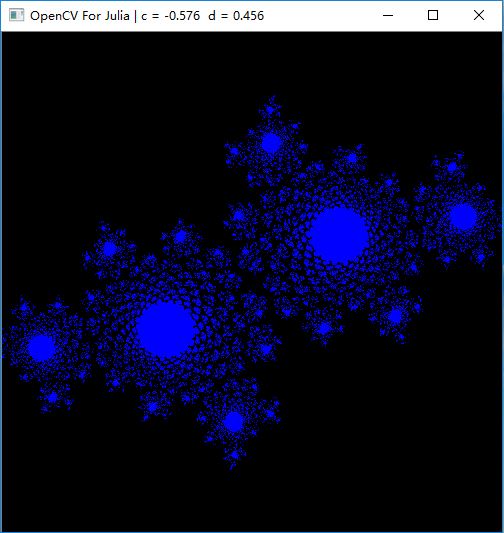
c=-0.576 d=0.456:
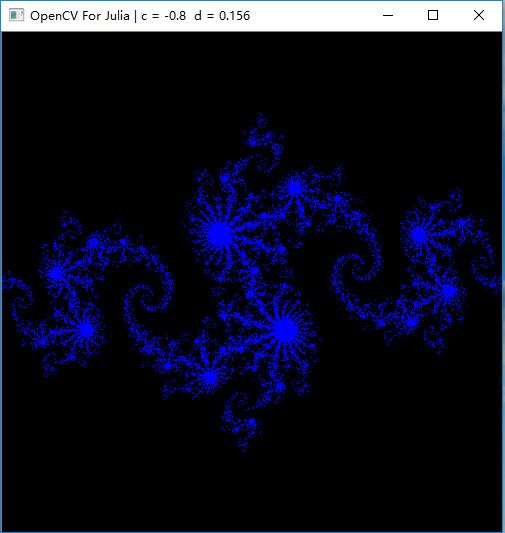
c=-0.8 d=0.156:
c=0.285 d=0.02:
c=-0.85 d=0.088:
OpenCV绘制朱利亚(Julia)集合图形的更多相关文章
- CUDA+OpenCV 绘制朱利亚(Julia)集合图形
Julia集中的元素都是经过简单的迭代计算得到的,很适合用CUDA进行加速.对一个600*600的图像,需要进行360000次迭代计算,所以在CUDA中创建了600*600个线程块(block),每个 ...
- 混沌分形之朱利亚集(JuliaSet)
朱利亚集合是一个在复平面上形成分形的点的集合.以法国数学家加斯顿·朱利亚(Gaston Julia)的名字命名.我想任何一个有关分形的资料都不会放过曼德勃罗集和朱利亚集.这里将以点集的方式生成出朱利亚 ...
- 详解用OpenCV绘制各类几何图形
摘要:本文详细介绍了OpenCV绘制几何图形的方法,利用cv2.line().v2.circle().cv2.rectangle().cv2.ellipse().cv2.polylines().cv2 ...
- Linux命令之dot - 绘制DOT语言脚本描述的图形
本文链接:http://codingstandards.iteye.com/blog/840055 用途说明 Graphviz (Graph Visualization Software的缩写)是一个 ...
- C# winform如何清除由Graphics类绘制出来的所有线条或图形
在C#winform应用程序中,可以用GDI绘制出线条或图形. 1.在主窗体上绘制线条或图形 using (Graphics g = this.CreateGraphics()) { ...
- Turtle绘制带颜色和字体的图形(Python3)
转载自https://blog.csdn.net/wumenglu1018/article/details/78184930 在Python中有很多编写图形程序的方法,一个简单的启动图形化程序设计的方 ...
- 绘制播放音乐时的音波图形的View
绘制播放音乐时的音波图形的View 这个效果类似于这个哦: 效果如下: 源码: MusicView.h 与 MusicView.m // // MusicView.h // Music // // C ...
- OpenCV绘制检测结果
OpenCV绘制检测结果 opencv rtcp timestamp 一.介绍 由于在验证阶段,使用FPGA时我们的算法检测速度很慢,没法直接在主流上进行绘图,否则的话,主流就要等待算法很久才能 ...
- [CTF]维吉尼亚密码(维基利亚密码)
[CTF]维吉尼亚密码(维基利亚密码) ----------------------百度百科 https://baike.baidu.com/item/维吉尼亚密码/4905472?fr=aladdi ...
随机推荐
- Leetcode之Best Time to Buy and Sell Stock
Say you have an array for which the ith element is the price of a given stock on day i. If you were ...
- Mosquito的优化——订阅树优化(八)
本文由逍遥子撰写.转发请标注原址: http://blog.csdn.net/houjixin/article/details/46413783 或 http://houjixin.blog.163. ...
- 多类 SVM 的损失函数及其梯度计算
CS231n Convolutional Neural Networks for Visual Recognition -- optimization 1. 多类 SVM 的损失函数(Multicla ...
- 学习redis--安装(二)
安装前准备,我是在虚拟机中安装centos,然后安装redis. 安装 1.安装VMware,并安转centos系统 2.将redis的压缩包,上传到linux系统中(将下载到pc中的文件,拖到cen ...
- Java文档上传问题设计
近期公司让做一个文档上传的功能,功能描写叙述大概是这样子滴 书籍名称.书籍定价.书籍封面图片(须要上传).文档内容 (须要上传) .还有其它相关的描写叙述信息. 我的设计 表 A 包括以上字段 , ...
- stm32的DMA重新工作
下面是在战舰V3寄存器程序例子中找到的: //开启一次DMA传输void MYDMA_Enable(DMA_Channel_TypeDef*DMA_CHx){ DMA_CHx->CCR&a ...
- 积跬步,聚小流------java获取图片的尺寸
在一篇文章中获取到通过例如以下两种方式进行获取: 1.使用ImageReader进行获取: 2.使用BufferedImage进行获取: 而且经过验证ImageReader进行操作的耗时远远低于Buf ...
- php实现 字符串加密(分类分布分工,化不可能为可能)
php实现 字符串加密(分类分布分工,化不可能为可能) 一.总结 一句话总结:谋而后动,加先伪代码,在带函数逻辑,在函数的方式可以极大的避免错误和降低难度.不然这个题目乎出现各种乱七八糟的错误. 1 ...
- oracle员工表和部门表基本操作
emp 员工表(empno 员工号/ename 员工姓名/job 工作/mgr 上级编号/hiredate 受雇日期/sal 薪金/comm 佣金/deptno 部门编号) dept 部门表(dept ...
- [Compose] 10. Capture Side Effects in a Task
We examine the data structure Task, see some constructors, familiar methods, and finally how it capt ...