expectation-maximization algorithm ---- PRML读书笔记
An elegant and powerful method for finding maximum likelihood solutions for models with latent variables is called the expectation-maximization algorithm, or EM algorithm.
If we assume that the data points are drawn independently from the distribution, then the log of the likelihood function is given by
lnp(X|π,μ,Σ)=Σnln{ΣkπkN(xn|μk,Σk)}
EM for Gaussian Mixtures
Given a Gaussian mixture model, the goal is to maximize the likelihood function with respect to the parameters(comprising the means and covariances of the components
and the mixing coefficients).
1.Initialize the means μk, covariances Σk and mixing coefficients πk, and evaluate the initial value of the log likelihood.
2.E step. Evaluate the responsibilities using the current parameter values
3.M step. Re-estimate the parameters using the current responsibilities.
4.Evaluate the log likelihood
lnp(X|π,μ,Σ)=Σnln{ΣkπkN(xn|μk,Σk)}
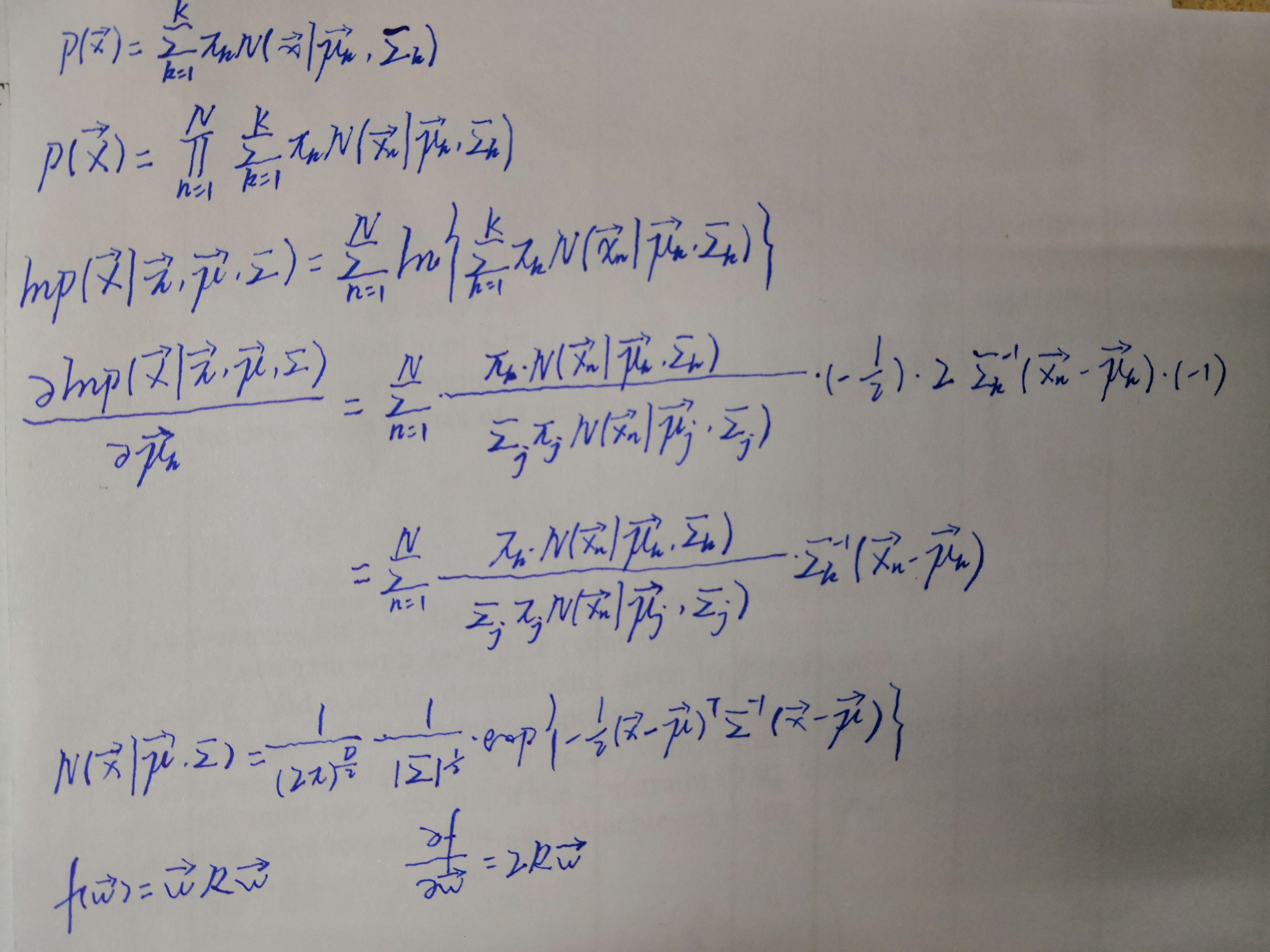
expectation-maximization algorithm ---- PRML读书笔记的更多相关文章
- EM算法(Expectation Maximization Algorithm)
EM算法(Expectation Maximization Algorithm) 1. 前言 这是本人写的第一篇博客(2013年4月5日发在cnblogs上,现在迁移过来),是学习李航老师的< ...
- EM算法(Expectation Maximization Algorithm)初探
1. 通过一个简单的例子直观上理解EM的核心思想 0x1: 问题背景 假设现在有两枚硬币Coin_a和Coin_b,随机抛掷后正面朝上/反面朝上的概率分别是 Coin_a:P1:-P1 Coin_b: ...
- [转]EM算法(Expectation Maximization Algorithm)详解
https://blog.csdn.net/zhihua_oba/article/details/73776553 EM算法(Expectation Maximization Algorithm)详解 ...
- PRML读书笔记——2 Probability Distributions
2.1. Binary Variables 1. Bernoulli distribution, p(x = 1|µ) = µ 2.Binomial distribution + 3.beta dis ...
- PRML读书笔记——3 Linear Models for Regression
Linear Basis Function Models 线性模型的一个关键属性是它是参数的一个线性函数,形式如下: w是参数,x可以是原始的数据,也可以是关于原始数据的一个函数值,这个函数就叫bas ...
- PRML读书笔记——Mathematical notation
x, a vector, and all vectors are assumed to be column vectors. M, denote matrices. xT, a row vcetor, ...
- PRML读书笔记——机器学习导论
什么是模式识别(Pattern Recognition)? 按照Bishop的定义,模式识别就是用机器学习的算法从数据中挖掘出有用的pattern. 人们很早就开始学习如何从大量的数据中发现隐藏在背后 ...
- PRML读书笔记_绪论
一.基本名词 泛化(generalization) 训练集所训练的模型对新数据的适用程度. 监督学习(supervised learning) 训练数据的样本包含输入向量以及对应的目标向量. 分类( ...
- Expectation Maximization Algorithm
期望最大化算法EM. 简介 EM算法即期望最大化算法,由Dempster等人在1976年提出[1].这是一种迭代法,用于求解含有隐变量的最大似然估计.最大后验概率估计问题.至于什么是隐变量,在后面会详 ...
随机推荐
- jQuery——val()、text()、html()
val():获取标签中的value属性的值.带有参数是赋值(类比js中的value属性) text():获取双闭合标签中的文本值.(不识别标签)(类比innerText) html():获取双闭合标签 ...
- servlet-响应的定时刷新
package servlet; import java.io.IOException; import javax.servlet.ServletException; import javax.ser ...
- 設置VS2015
減少VsHub的資源占用 VsHub在某些環境下會挂,原因見這個帖子 其作用簡述如下: First, the service that detects and auto-updates extensi ...
- Apache、Nginx与Tomcat的区别
一. 定义: 1. Apache Apache HTTP服务器是一个模块化的服务器,可以运行在几乎所有广泛使用的计算机平台上.其属于应用服务器.Apache支持支持模块多,性能稳定,A ...
- 如何用windbg查看_eprocess结构
打开菜单: File->Symbol File Path... 输入: C:/MyCodesSymbols; SRV*C:/MyLocalSymbols*http://msdl.microsof ...
- CAD在图纸保存的同时,也把基本信息保存了(网页版)
主要用到函数说明: MxDrawXCustomFunction::Mx_SaveDwgToURLEx 保存DWG文件到服务器上的扩展函数.详细说明如下: 参数 说明 pszServerUrl 服务器网 ...
- Python os模块和time模块 day4
一.os模块 print(os.listdir(r'/Users/smh/Desktop/整理'))#os.listdir() 列出某个目录下面的文件夹/文件 print(os.path.isfile ...
- JavaScript初步学习----基本使用,简单事件,修改样式,数据类型
JavaScript基本使用 JavaScript原名叫livescript,是一门动态类型,弱类型基于原型的脚本语言 用于页面特效,前后交替,后台开发(node) JavaScript写在s ...
- 如何实现在scrapy调试爬虫
# -*- coding:utf-8 -*- from scrapy.cmdline import execute import sys import os '''在爬虫文件夹下面自定义一个main. ...
- [网络流24题#9] [cogs734] 方格取数 [网络流,最大流最小割]
将网格分为两部分,方法是黑白染色,即判断(i+j)&1即可,分开后从白色格子向黑色格子连边,每个点需要四条(边界点可能更少),也就是每个格子周围的四个方向.之后将源点和汇点分别于黑白格子连边, ...
