【codeforces 719E】Sasha and Array

【题目链接】:http://codeforces.com/contest/719/problem/E

【题意】



给你一个数列,有两种操作1 l r x 给[l,r]区间上的数加上x, 2 l r 询问[l,r]区间fibonacci数列的和(f[l]+f[l+1]+……f[r])

【题解】



斐波那契数列有个矩阵乘法公式

f[n]=

[0 1] ^n× [0 0]
[1 1]     [0 1]

最后得到的矩阵A

A[1][2]就是答案;(即第一行第二列)



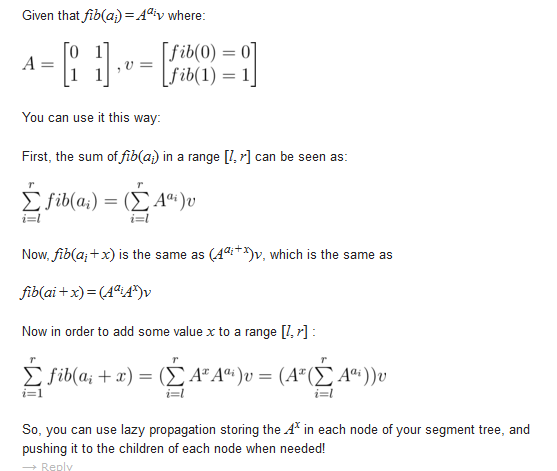
写个线段树的成段更新;

用懒惰标记记录加上的数字x对应的A^x

维护区间的矩阵和就好;

新增加的A^x不要每次都重新算，不然会T





【Number Of WA】



9



【完整代码】

#include <bits/stdc++.h>
using namespace std;
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define LL long long
#define rep1(i,a,b) for (int i = a;i <= b;i++)
#define rep2(i,a,b) for (int i = a;i >= b;i--)
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define ms(x,y) memset(x,y,sizeof x)
typedef pair<int,int> pii;
typedef pair<LL,LL> pll;
const int dx[9] = {0,1,-1,0,0,-1,-1,1,1};
const int dy[9] = {0,0,0,-1,1,-1,1,-1,1};
const double pi = acos(-1.0);
const int N = 1e5+100;
const int G = 2;       //�����С
const int MOD = 1e9 + 7;    //ģ��
struct MX
{
    LL v[G+1][G+1];
    void O() { ms(v, 0); }
    void E() { ms(v, 0); for (int i = 1; i <= G; ++i)v[i][i] = 1; }
    MX operator * (const MX &b) const
    {
        MX c; c.O();
        for (int k = 1; k <= G; ++k)
        {
            for (int i = 1; i <= G; ++i) if (v[i][k])
            {
                for (int j = 1; j <= G; ++j)
                {
                    c.v[i][j] = (c.v[i][j] + (LL)v[i][k] * b.v[k][j]) % MOD;
                }
            }
        }
        return c;
    }
    MX operator + (const MX &b) const
    {
        MX c; c.O();
        for (int i = 1; i <= G; ++i)
        {
            for (int j = 1; j <= G; ++j)
            {
                c.v[i][j] = (v[i][j] + b.v[i][j]) % MOD;
            }
        }
        return c;
    }
    MX operator ^ (LL p) const
    {
        MX y; y.E();
        MX x; memcpy(x.v, v, sizeof(v));
        while (p)
        {
            if (p&1) y = y*x;
            x = x*x;
            p>>=1;
        }
        return y;
    }
}A,v,cur;
int n,m,flag[N<<2];
MX sum[N<<2],lazy_tag[N<<2];
LL a[N];
inline void push_up(int rt)
{
    sum[rt] = sum[rt<<1] + sum[rt<<1|1];
}
void build(int l,int r,int rt)
{
    lazy_tag[rt].E();
    if (l==r)
    {
        sum[rt] = A^a[l];
        return;
    }
    int m = (l+r)>>1;
    build(lson),build(rson);
    push_up(rt);
}
inline void push_down(int rt)
{
    if (!flag[rt]) return;
    flag[rt<<1] = flag[rt<<1|1] = 1;
    flag[rt] = 0;
    sum[rt<<1]=sum[rt<<1]*lazy_tag[rt];
    sum[rt<<1|1]=sum[rt<<1|1]*lazy_tag[rt];
    lazy_tag[rt<<1] = lazy_tag[rt<<1]*lazy_tag[rt];
    lazy_tag[rt<<1|1] = lazy_tag[rt<<1|1]*lazy_tag[rt];
    lazy_tag[rt].E();
}
void up_data(int L,int R,int x,int l,int r,int rt)
{
    if (L<= l && r <= R)
    {
        lazy_tag[rt]=lazy_tag[rt]*cur;
        sum[rt] = sum[rt]*cur;
        flag[rt] = 1;
        return;
    }
    push_down(rt);
    int m = (l+r)>>1;
    if (L <= m) up_data(L,R,x,lson);
    if (m < R) up_data(L,R,x,rson);
    push_up(rt);
}
MX Q(int L,int R,int l,int r,int rt)
{
    if (L <= l && r <= R)
        return sum[rt];
    push_down(rt);
    int m = (l+r)>>1;
    MX temp1,temp2;
    temp1.O(),temp2.O();
    if (L <= m) temp1 = Q(L,R,lson);
    if (m < R) temp2 = Q(L,R,rson);
    temp1 = temp1 + temp2;
    return temp1;
}
LL query(int l,int r)
{
    MX temp = Q(l,r,1,n,1);
    temp = temp*v;
    return temp.v[1][2];
}
int main()
{
    //freopen("F:\\rush.txt","r",stdin);
    ios::sync_with_stdio(false),cin.tie(0);//scanf,puts,printf not use
    cin >> n >> m;
    rep1(i,1,n) cin >> a[i];
    A.v[1][1] = 0,A.v[1][2] = A.v[2][1] = A.v[2][2] = 1;
    v.v[1][1] = v.v[1][2] = v.v[2][1] = 0,v.v[2][2] = 1;
    build(1,n,1);
    rep1(i,1,m)
    {
        int type;
        cin >> type;
        if (type==1)
        {
            int l,r,x;
            cin >> l >> r >> x;
            cur = A^x;
            up_data(l,r,x,1,n,1);
        }
        else
        {
            int l,r;
            cin >> l >> r;
            cout << query(l,r) << endl;
        }
    }
    return 0;
}