紫书 习题 8-25 UVa 11175 （结论证明）（配图）

看了这篇博客https://blog.csdn.net/u013520118/article/details/48032599

但是这篇里面没有写结论的证明， 我来证明一下。

首先结论是对于E图而言，如果存在i和j结点到k1都有边，而i和j中只有一个结点到k2有边，则这个图是不可能转化来的。

首先先讲E图中i和j结点到k1都有边， 那么图会是怎么样的呢？有三种情况

大家可以发现，在D图中，  i边的起点和j边的起点无论如何都会连在同一个点上， 那么， 假设i边起点为i0， j变起点为j0，

都连在p点上。

那么在E图中如果i和j其中一个点， 比如i点， 有另外一条边连到k2的话

那也就是说在D图中i边的终点p多了一条连向其他点的边， 那么又因为j也连着p点， 所以在E图中必然有j到k2的一条边。

如图所示。

注意这个从p点出去的这个q点不一定是新的点， 也可以就是i点或者j点， 但是总之有一条边是以p点为起点的。

显然可以看到， 这个时候符合存在边jp和pq， 也就是说E图中必然还有一条边是j到k2的， 所以只要其中一个点

连到了k2， 那么另外一个点肯定存在边到k2， 不可能出现只有一个点连到k2的情况。

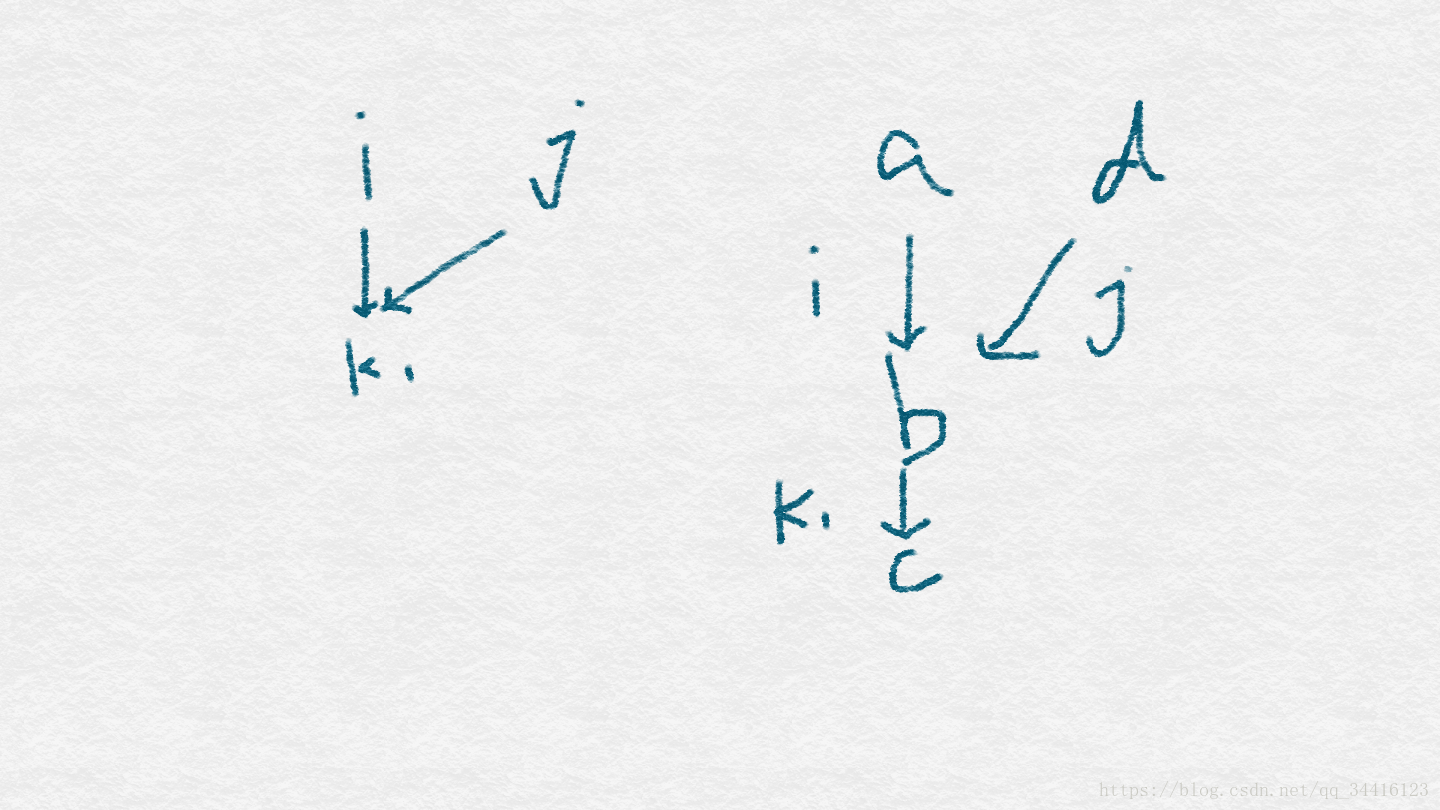
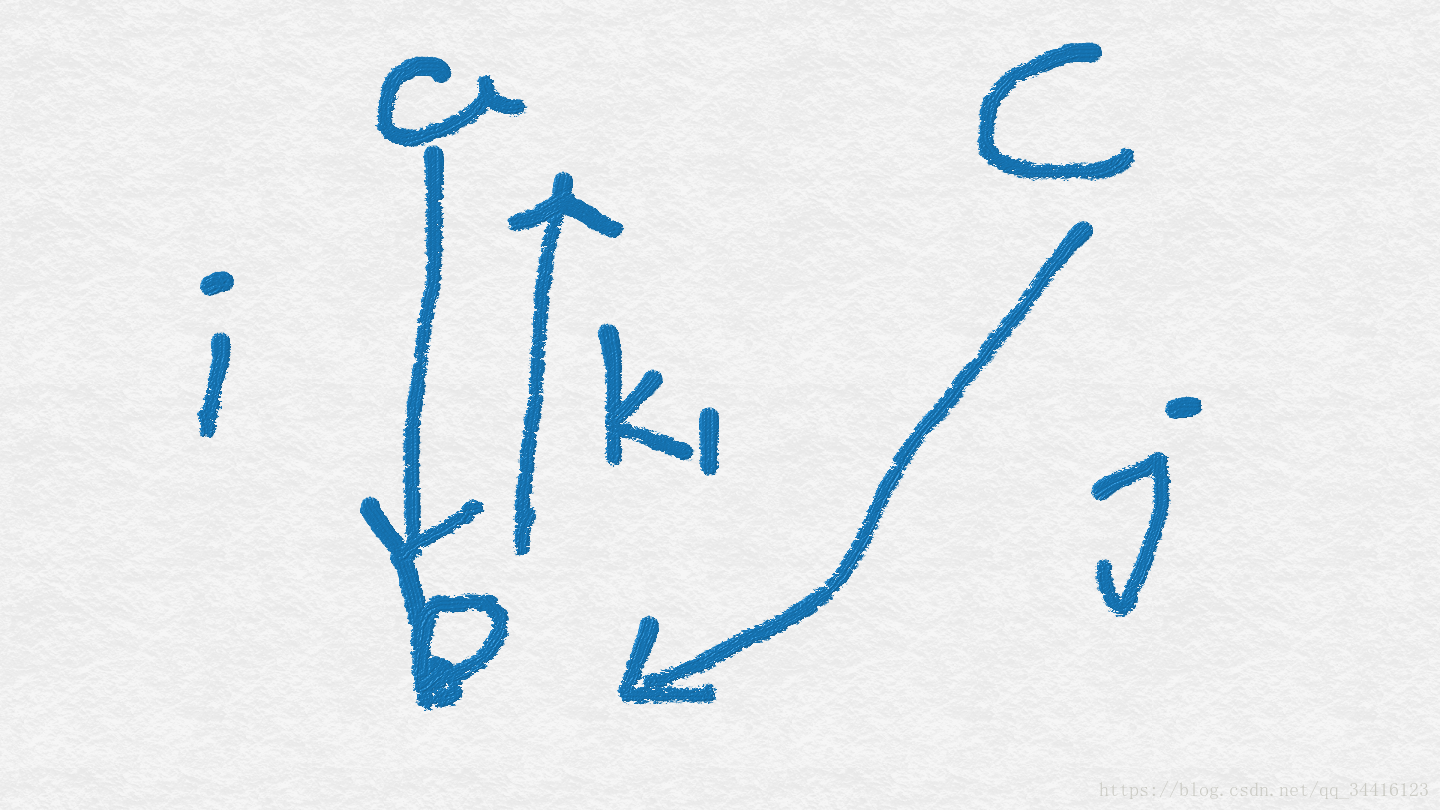
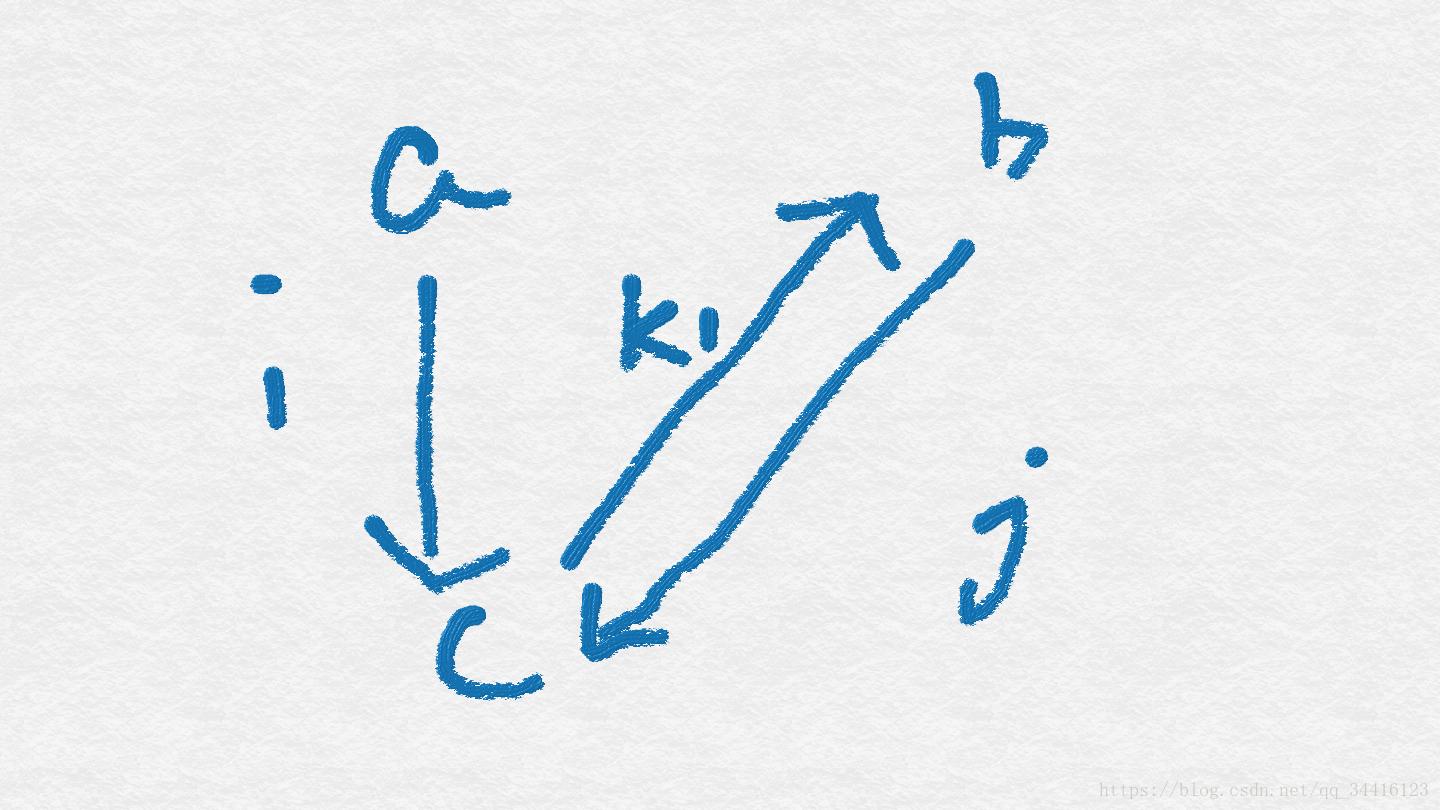
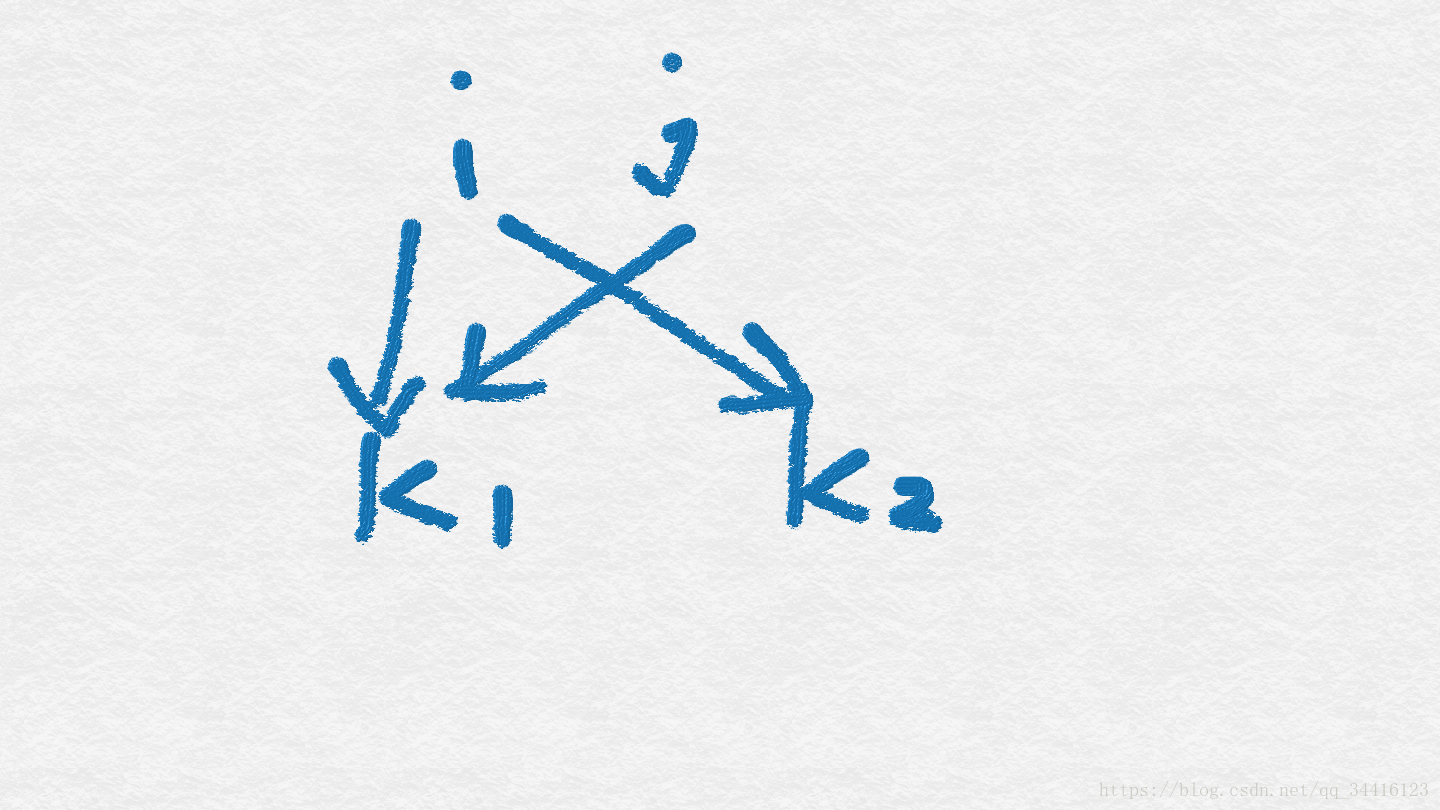
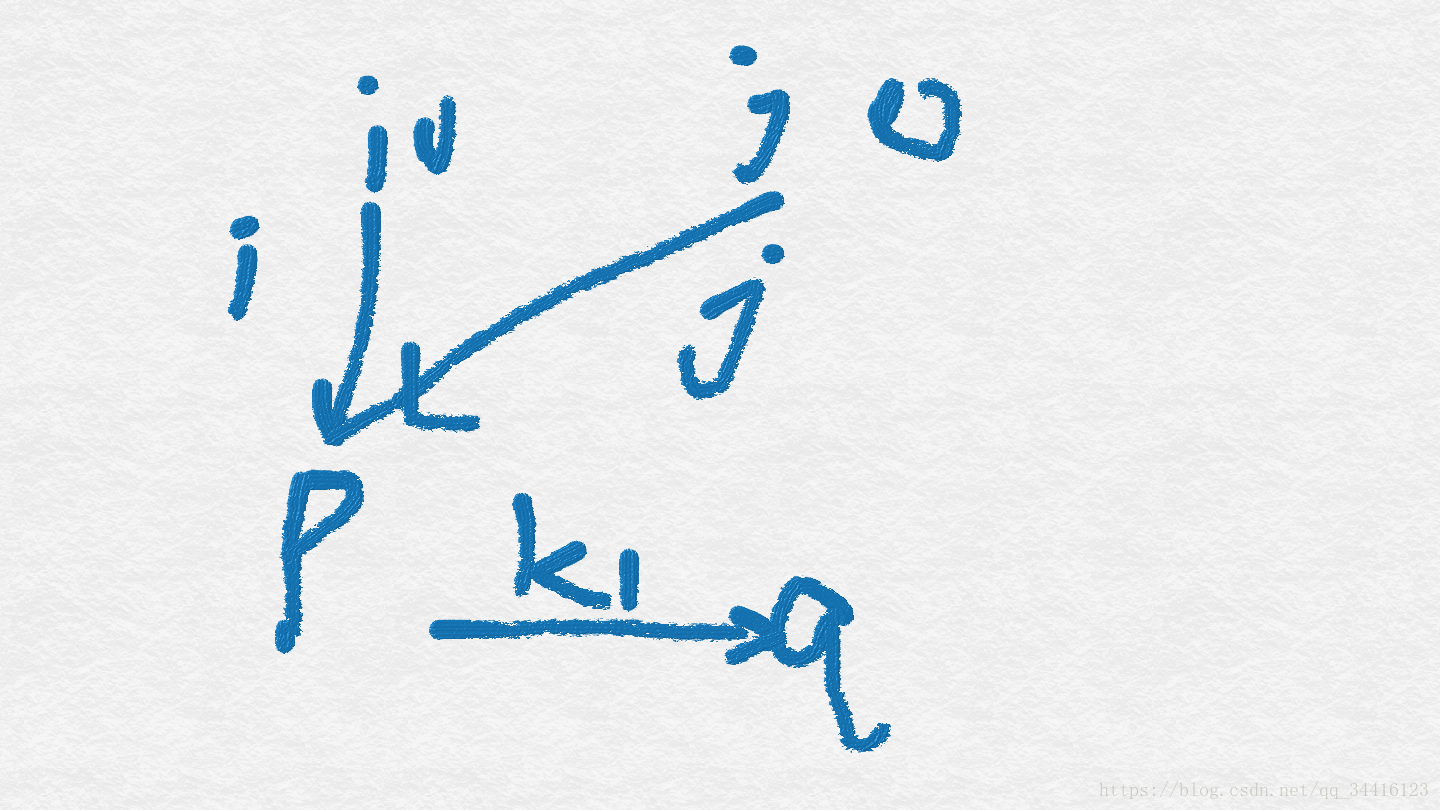
因此得出结论：对于E图而言，如果存在i和j结点到k1都有边，而i和j中只有一个结点到k2有边，则这个图是不可能转化来的。

#include<cstdio>
#include<cstring>
#define REP(i, a, b) for(int i = (a); i < (b); i++)
using namespace std;

const int MAXN = 312;
int g[MAXN][MAXN], n, m; 

bool judge()
{
	REP(i, 0, n)
		REP(j, 0, n)
		{
			bool ok1 = false, ok2 = false;
			REP(k, 0, n)
			{
				if(g[i][k] && g[j][k]) ok1 = true;
				if(g[i][k] ^ g[j][k]) ok2 = true;
			}
			if(ok1 && ok2) return false;
		}
	return true;
}

int main()
{
	int T, kase = 0;
	scanf("%d", &T);

	while(T--)
	{
		memset(g, 0, sizeof(g));
		scanf("%d%d", &n, &m);
		REP(i, 0, m)
		{
			int x, y;
			scanf("%d%d", &x, &y);
			g[x][y] = 1;
		}
		printf("Case #%d: %s\n", ++kase, judge() ? "Yes" : "No");
	}

	return 0;
}