A*专题训练

POJ2449 Remmarguts' Date

UDF's capital consists of N stations. The hall is numbered S, while the station numbered T denotes prince' current place. M muddy directed sideways connect some of the stations. Remmarguts' path to welcome the princess might include the same station twice or more than twice, even it is the station with number S or T. Different paths with same length will be considered disparate. 1 <= N <= 1000, 0 <= M <= 100000 1 <= K <= 1000

K短路问题，直接dijkstra，第K次得到路经长的时候就是K短路。但是这样时间复杂度\(O(K M \log N)\)，不可接受。

考虑用A*算法提高搜索效率，反向预处理处节点\(x\)到终点的最短路长度\(f[x]\)，以\(dis+f[x]\)作为比较对象。显然\(f[x] \le g[x]\)。这样虽然时间复杂度上界没变，但是很多点的访问次数小于K，所以该算法能较为快速地求出结果。

#include<iostream>
#include<queue>
#include<cstring>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
    rg T data=0,w=1;
    rg char ch=getchar();
    while(!isdigit(ch)){
        if(ch=='-') w=-1;
        ch=getchar();
    }
    while(isdigit(ch))
        data=data*10+ch-'0',ch=getchar();
    return data*w;
}
template<class T>il T read(rg T&x){
    return x=read<T>();
}
typedef long long LL;
using namespace std;

co int N=1006;
int n,m,st,ed,k,f[N],cnt[N];
bool v[N];
vector<pair<int,int> > e[N],fe[N];
priority_queue<pair<int,int> > pq;
void dijkstra(){
    memset(f,0x3f,sizeof f);
    f[ed]=0;
    pq.push(make_pair(0,ed));
    while(pq.size()){
        int x=pq.top().second;
        pq.pop();
        if(v[x]) continue;
        v[x]=1;
        for(unsigned i=0;i<fe[x].size();++i){
            int y=fe[x][i].first,z=fe[x][i].second;
            if(f[y]>f[x]+z){
                f[y]=f[x]+z;
                pq.push(make_pair(-f[y],y));
            }
        }
    }
}
void A_star(){
    if(st==ed) ++k;
    pq.push(make_pair(-f[st],st));
    while(pq.size()){
        int x=pq.top().second;
        int dist=-pq.top().first-f[x];
        pq.pop();
        ++cnt[x];
        if(cnt[ed]==k){
            printf("%d\n",dist);
            return;
        }
        for(unsigned i=0;i<e[x].size();++i){
            int y=e[x][i].first,z=e[x][i].second;
            if(cnt[y]!=k) pq.push(make_pair(-f[y]-dist-z,y));
        }
    }
    puts("-1");
}
int main(){
//  freopen(".in","r",stdin);
//  freopen(".out","w",stdout);
    read(n),read(m);
    for(int i=1,x,y,z;i<=m;++i){
        read(x),read(y),read(z);
        e[x].push_back(make_pair(y,z)),fe[y].push_back(make_pair(x,z));
    }
    read(st),read(ed),read(k);
    dijkstra();
    A_star();
    return 0;
}

POJ1077 Eight

The 15-puzzle has been around for over 100 years; even if you don't know it by that name, you've seen it. It is constructed with 15 sliding tiles, each with a number from 1 to 15 on it, and all packed into a 4 by 4 frame with one tile missing. Let's call the missing tile 'x'; the object of the puzzle is to arrange the tiles so that they are ordered as:

 1  2  3  4

 5  6  7  8

 9 10 11 12

13 14 15  x 

where the only legal operation is to exchange 'x' with one of the tiles with which it shares an edge. As an example, the following sequence of moves solves a slightly scrambled puzzle:

 1  2  3  4    1  2  3  4    1  2  3  4    1  2  3  4

 5  6  7  8    5  6  7  8    5  6  7  8    5  6  7  8

 9  x 10 12    9 10  x 12    9 10 11 12    9 10 11 12

13 14 11 15   13 14 11 15   13 14  x 15   13 14 15  x

           r->           d->           r-> 

The letters in the previous row indicate which neighbor of the 'x' tile is swapped with the 'x' tile at each step; legal values are 'r','l','u' and 'd', for right, left, up, and down, respectively.



Not all puzzles can be solved; in 1870, a man named Sam Loyd was famous for distributing an unsolvable version of the puzzle, and

frustrating many people. In fact, all you have to do to make a regular puzzle into an unsolvable one is to swap two tiles (not counting the missing 'x' tile, of course).



In this problem, you will write a program for solving the less well-known 8-puzzle, composed of tiles on a three by three

arrangement.

八数码问题，用康托展开记录状态，在A*算法中，用当前状态中所有数字的位置与目标状态中所有数字的位置的曼哈顿距离之和来做估值函数。另外可以用逆序对数奇偶性相同判无解。

#include<iostream>
#include<cmath>
#include<queue>
#include<cstring>
#include<string>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
    rg T data=0,w=1;
    rg char ch=getchar();
    while(!isdigit(ch)){
        if(ch=='-') w=-1;
        ch=getchar();
    }
    while(isdigit(ch))
        data=data*10+ch-'0',ch=getchar();
    return data*w;
}
template<class T>il T read(rg T&x){
    return x=read<T>();
}
typedef long long LL;
using namespace std;

co int N=362886;
int fa[N],f[N];
bool v[N];
co int dx[4]={-1,0,1,0},dy[4]={0,-1,0,1};
co int jc[10]={1,1,2,6,24,120,720,5040,40320,362880};
struct P{
    int i,x,y;
    string s;
    P(){}
    P(int i,int x,int y,string s):i(i),x(x),y(y),s(s){}
    bool operator<(co P a)co{
        return x+y>a.x+a.y;
    }
};
priority_queue<P> q;
int cantor(string st){
    int len=st.size();
    for(int i=0;i<len;++i)
        if(st[i]=='x'){
            st[i]='0';
            break;
        }
    int ans=1;
    for(int i=0;i<len;++i){
        int num=0;
        for(int j=0;j<i;++j) if(st[j]<st[i]) ++num;
        ans+=(st[i]-'0'-num)*jc[len-i-1];
    }
    return ans;
}
int S(string s){
    int ans=0;
    for(unsigned i=0;i<s.size();++i){
        int r=i/3,c=i%3;
        if(s[i]=='x') ans+=abs(r-2)+abs(c-2);
        else{
            int k=s[i]-'1';
            ans+=abs(r-k/3)+abs(c-k%3);
        }
    }
    return ans;
}
bool bfs(string st){
    string ed="12345678x";
    memset(fa,-1,sizeof fa);
    memset(f,-1,sizeof f);
    int k;
    for(int i=0;i<10;++i)
        if(st[i]=='x'){
            k=i;
            break;
        }
    P p=P(k,0,S(st),st);
    q.push(p);
    v[cantor(st)]=1;
    while(q.size()){
        p=q.top();
        if(p.s==ed) return 1;
        q.pop();
        int r=p.i/3,c=p.i%3;
        for(int i=0;i<4;++i){
            int nx=r+dx[i],ny=c+dy[i];
            if(nx<0||nx>2||ny<0||ny>2) continue;
            string s=p.s;
            swap(s[p.i],s[nx*3+ny]);
            int k=cantor(s);
            if(v[k]) continue;
            v[k]=1,fa[k]=cantor(p.s),f[k]=i;
            P np=P(nx*3+ny,p.x+1,S(s),s);
            q.push(np);
        }
    }
    return 0;
}
int main(){
//  freopen(".in","r",stdin);
//  freopen(".out","w",stdout);
    string st="";
    for(int i=1;i<=9;++i){
        char s[2];
        scanf("%s",s);
        st+=s[0];
    }
    int cnt=0;
    for(unsigned i=0;i<st.size();++i) if(st[i]!='x')
        for(unsigned j=0;j<i;++j)
            if(st[j]!='x'&&st[j]>st[i]) ++cnt;
    if(cnt&1){
        puts("unsolvable");
        return 0;
    }
    vector<int> ans;
    if(bfs(st)){
        int k=cantor("12345678x");
        while(k!=-1){
            ans.push_back(f[k]);
            k=fa[k];
        }
        for(unsigned i=ans.size()-1;i<ans.size();--i) // correct due to unsigned
            if(ans[i]==0) putchar('u');
            else if(ans[i]==1) putchar('l');
            else if(ans[i]==2) putchar('d');
            else if(ans[i]==3) putchar('r');
    }else puts("unsolvable");
    return 0;
}

POJ3460 Booksort

The Leiden University Library has millions of books. When a student wants to borrow a certain book, he usually submits an online loan form. If the book is available, then the next day the student can go and get it at the loan counter. This is the modern way of borrowing books at the library.

There is one department in the library, full of bookcases, where still the old way of borrowing is in use. Students can simply walk around there, pick out the books they like and, after registration, take them home for at most three weeks.

Quite often, however, it happens that a student takes a book from the shelf, takes a closer look at it, decides that he does not want to read it, and puts it back. Unfortunately, not all students are very careful with this last step. Although each book has a unique identification code, by which the books are sorted in the bookcase, some students put back the books they have considered at the wrong place. They do put it back onto the right shelf. However, not at the right position on the shelf.

Other students use the unique identification code (which they can find in an online catalogue) to find the books they want to borrow. For them, it is important that the books are really sorted on this code. Also for the librarian, it is important that the books are sorted. It makes it much easier to check if perhaps some books are stolen: not borrowed, but yet missing.

Therefore, every week, the librarian makes a round through the department and sorts the books on every shelf. Sorting one shelf is doable, but still quite some work. The librarian has considered several algorithms for it, and decided that the easiest way for him to sort the books on a shelf, is by sorting by transpositions: as long as the books are not sorted,

1. take out a block of books (a number of books standing next to each other),
2. shift another block of books from the left or the right of the resulting ‘hole’, into this hole,
3. and put back the first block of books into the hole left open by the second block.

One such sequence of steps is called a transposition.

The following picture may clarify the steps of the algorithm, where X denotes the first block of books, and Y denotes the second block.

Original situation:
After step 1:
After step 2:
After step 3:

Of course, the librarian wants to minimize the work he has to do. That is, for every bookshelf, he wants to minimize the number of transpositions he must carry out to sort the books. In particular, he wants to know if the books on the shelf can be sorted by at most 4 transpositions. Can you tell him?

考虑搜索，每一层有\(\sum_{i=1}^n (n-i+1)(n-i)=560\)种分支，不能全部搜完，所以要剪枝。由于一次操作最多让3个数的后继变对，所以操作次数至少是后继不对的数的个数除以3上取整，利用这个性质来剪枝。显然要用迭代搜索，所以这是一个IDA*算法。

#include<iostream>
#include<cstring>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
    rg T data=0,w=1;
    rg char ch=getchar();
    while(!isdigit(ch)){
        if(ch=='-') w=-1;
        ch=getchar();
    }
    while(isdigit(ch))
        data=data*10+ch-'0',ch=getchar();
    return data*w;
}
template<class T>il T read(rg T&x){
    return x=read<T>();
}
typedef long long LL;

co int N=20;
int n,a[N],dep;
int gj(){
    int cnt=0;
    for(int i=1;i<n;++i)
        if(a[i]+1!=a[i+1]) ++cnt;
    if(a[n]!=n) return cnt;
    return cnt;
}
void work(int l,int r,int t){
    int b[N],p=r;
    for(int i=l;i<=t;++i){
        b[i]=a[++p];
        if(p==t) p=l-1;
    }
    for(int i=l;i<=t;++i) a[i]=b[i];
}
bool dfs(int now){
    int cnt=gj();
    if(!cnt) return 1;
    if(3*now+cnt>3*dep) return 0;
    int c[N];
    memcpy(c,a,sizeof c);
    for(int l=1;l<=n;++l)
        for(int r=l;r<=n;++r)
            for(int t=r+1;t<=n;++t){
                work(l,r,t);
                if(dfs(now+1)) return 1;
                memcpy(a,c,sizeof a);
            }
    return 0;
}
void Booksort(){
    read(n);
    for(int i=1;i<=n;++i) read(a[i]);
    for(dep=0;dep<=4;++dep)
        if(dfs(0)){
            printf("%d\n",dep);
            return;
        }
    puts("5 or more");
}
int main(){
//  freopen(".in","r",stdin);
//  freopen(".out","w",stdout);
    int t=read<int>();
    while(t--) Booksort();
    return 0;
}

POJ2286 The Rotation Game

The rotation game uses a # shaped board, which can hold 24 pieces of square blocks (see Fig.1). The blocks are marked with symbols 1, 2 and 3, with exactly 8 pieces of each kind.



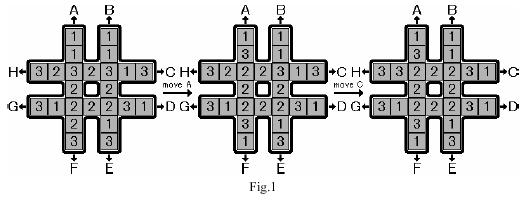
Initially, the blocks are placed on the board randomly. Your task is to move the blocks so that the eight blocks placed in the center square have the same symbol marked. There is only one type of valid move, which is to rotate one of the four lines, each consisting of seven blocks. That is, six blocks in the line are moved towards the head by one block and the head block is moved to the end of the line. The eight possible moves are marked with capital letters A to H. Figure 1 illustrates two consecutive moves, move A and move C from some initial configuration.

要字典序最小，考虑迭代加深搜索，剪枝优化：

1. 每次不做上一次操作的逆操作
2. 当前中央8格中最多的数字为k，其他的数字有m个，至少要做m次操作才能将这m个数字都换成k。

 #include<iostream>
#include<cstring>
#include<vector>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
    rg T data=0,w=1;
    rg char ch=getchar();
    while(!isdigit(ch)){
        if(ch=='-') w=-1;
        ch=getchar();
    }
    while(isdigit(ch))
        data=data*10+ch-'0',ch=getchar();
    return data*w;
}
template<class T>il T read(rg T&x){
    return x=read<T>();
}
typedef long long LL;
using namespace std;

int a[9][9],dep;
vector<char> ans;
void work(int k){
    if(k==1){
        for(int i=1;i<8;++i) a[i-1][3]=a[i][3];
        a[7][3]=a[0][3];
    }else if(k==2){
        for(int i=1;i<8;++i) a[i-1][5]=a[i][5];
        a[7][5]=a[0][5];
    }else if(k==3){
        for(int i=7;i;--i) a[3][i+1]=a[3][i];
        a[3][1]=a[3][8];
    }else if(k==4){
        for(int i=7;i;--i) a[5][i+1]=a[5][i];
        a[5][1]=a[5][8];
    }else if(k==5){
        for(int i=7;i;--i) a[i+1][5]=a[i][5];
        a[1][5]=a[8][5];
    }else if(k==6){
        for(int i=7;i;--i) a[i+1][3]=a[i][3];
        a[1][3]=a[8][3];
    }else if(k==7){
        for(int i=1;i<8;++i) a[5][i-1]=a[5][i];
        a[5][7]=a[5][0];
    }else{
        for(int i=1;i<8;++i) a[3][i-1]=a[3][i];
        a[3][7]=a[3][0];
    }
}
int gj(){
    int num[4];
    num[1]=num[2]=num[3]=0;
    for(int i=3;i<6;++i)
        for(int j=3;j<6;++j){
            if(i==4&&j==4) continue;
            ++num[a[i][j]];
        }
    return 8-max(num[1],max(num[2],num[3]));
}
bool dfs(int now){
    int cnt=gj();
    if(!cnt) return 1;
    if(now+cnt>dep) return 0;
    int b[9][9];
    memcpy(b,a,sizeof b);
    for(int i=1;i<9;++i){
        if(ans.size()){
            int k=ans.back();
            if(k-'A'+1==1&&i==6) continue;
            if(k-'A'+1==2&&i==5) continue;
            if(k-'A'+1==3&&i==8) continue;
            if(k-'A'+1==4&&i==7) continue;
            if(k-'A'+1==5&&i==2) continue;
            if(k-'A'+1==6&&i==1) continue;
            if(k-'A'+1==7&&i==4) continue;
            if(k-'A'+1==8&&i==3) continue;
        }
        ans.push_back(i+'A'-1);
        work(i);
        if(dfs(now+1)) return 1;
        ans.pop_back();
        memcpy(a,b,sizeof a);
    }
    return 0;
}
void The_Rotation_Game(){
    read(a[1][5]),read(a[2][3]),read(a[2][5]);
    for(int i=1;i<8;++i) read(a[3][i]);
    read(a[4][3]),read(a[4][5]);
    for(int i=1;i<8;++i) read(a[5][i]);
    read(a[6][3]),read(a[6][5]),read(a[7][3]),read(a[7][5]);
    ans.clear();
    dep=0;
    while(!dfs(0)) ++dep;
    if(!dep) puts("No moves needed");
    else{
        for(unsigned i=0;i<ans.size();++i)
            putchar(ans[i]);
        puts("");
    }
    printf("%d\n",a[3][3]);
}
int main(){
//  freopen(".in","r",stdin);
//  freopen(".out","w",stdout);
    while(read(a[1][3])) The_Rotation_Game();
    return 0;
}