20172329 2018-2019《Java软件结构与数据结构》第一周学习总结

2018-2019-20172329 《Java软件结构与数据结构》第一周学习总结

在这学期就已经大二了，也已经步入了学习专业课的核心时间，在这个阶段，我们应该了解自己的学习情况，针对自己的学习能力制定不同的计划，得到对于自我能力的提升。让我们开启新的一学期吧！

教材学习内容总结

Java 软件结构与数据结构第一章：概述

一、软件开发

1.软件工程：是一门关于高质量软件开发的技术和理论的学科。

2.解决的问题：控制开发过程，实现高质量的软件。

3.软件工程的目标：（1）解决正确性问题；（2）按时在预算之内给出解决方案；（3）给出高质量的解决方案；（4）以合情合理的方式完成上面事情。

4.软件质量的特征：（1）正确性（2）可靠性（3）健壮性（4）可用性（5）可维护性（6）可重复性（7）可移植性（8）运行效率

二、数据结构

1.程序=数据结构+算法；

小故事：Pascal之父——Nicklaus Wirth通过这一句话获得了图灵奖！

2.软件=程序+软件工程；

3.数据结构：计算机存储、组织数据的方式。

Java 软件结构与数据结构第二章：算法分析

一、算法效率分析

1.算法效率通常用CPU的使用时间表示；

2.算法分析是从效率的角度对算法进行分类；

3.增长函数表示与该问题大小相对应时间或空间的使用；

4.增长函数：（1）我们希望最优化的值；（2）通常关注的比较多是CPU的使用时间；（3）增长函数表示问题大小（n）与希望优化的值之间的关系。

二、大O记法

1.增长函数表示了该算法的时间复杂度或空间复杂度。

2.渐进复杂度称为算法的阶次。

注：

• （1）具有阶次为n^{2的时间复杂度，记为O(n}2)。
• （2）算法的阶次是忽略该算法的增长函数的常量和其他次要项，只保留主项。
• （3）不管问题是大是小，运行赋值语句和if语句一次，其复杂度就为 O(1)。
• （4）循环语句和方法调用语句可能会导致更高阶次的增长函数。
• （5）具有相同相同类别的两种算法，认为有相同的效率，但是其增长函数并不一定相同。
  
  3.例子：
  
  

三、增长函数的比较

1.更快的处理器，并不能影响主项，只会给增长函数增加常量，仍需要重视算法分析。

2例：



注：其中里面3.16、2.15、3.3的算法为，√10≈3.162277660168379、³√10≈2.1544、log2(10)=lg(10)/lg(2)=1/lg(2)=3.321928

3.n相对较小时，各种增长函数的比较

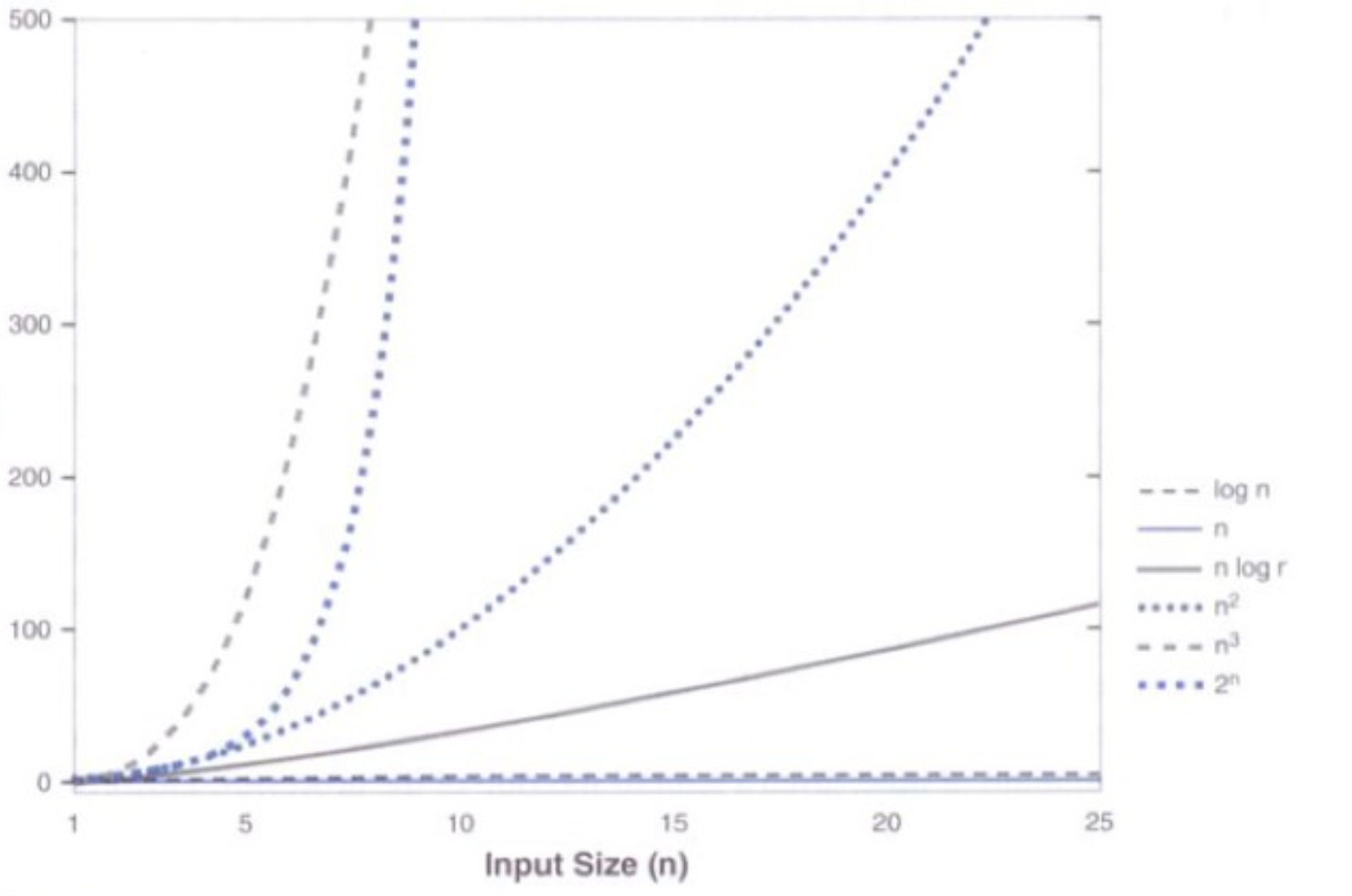
n很大时，各种增长函数的比较

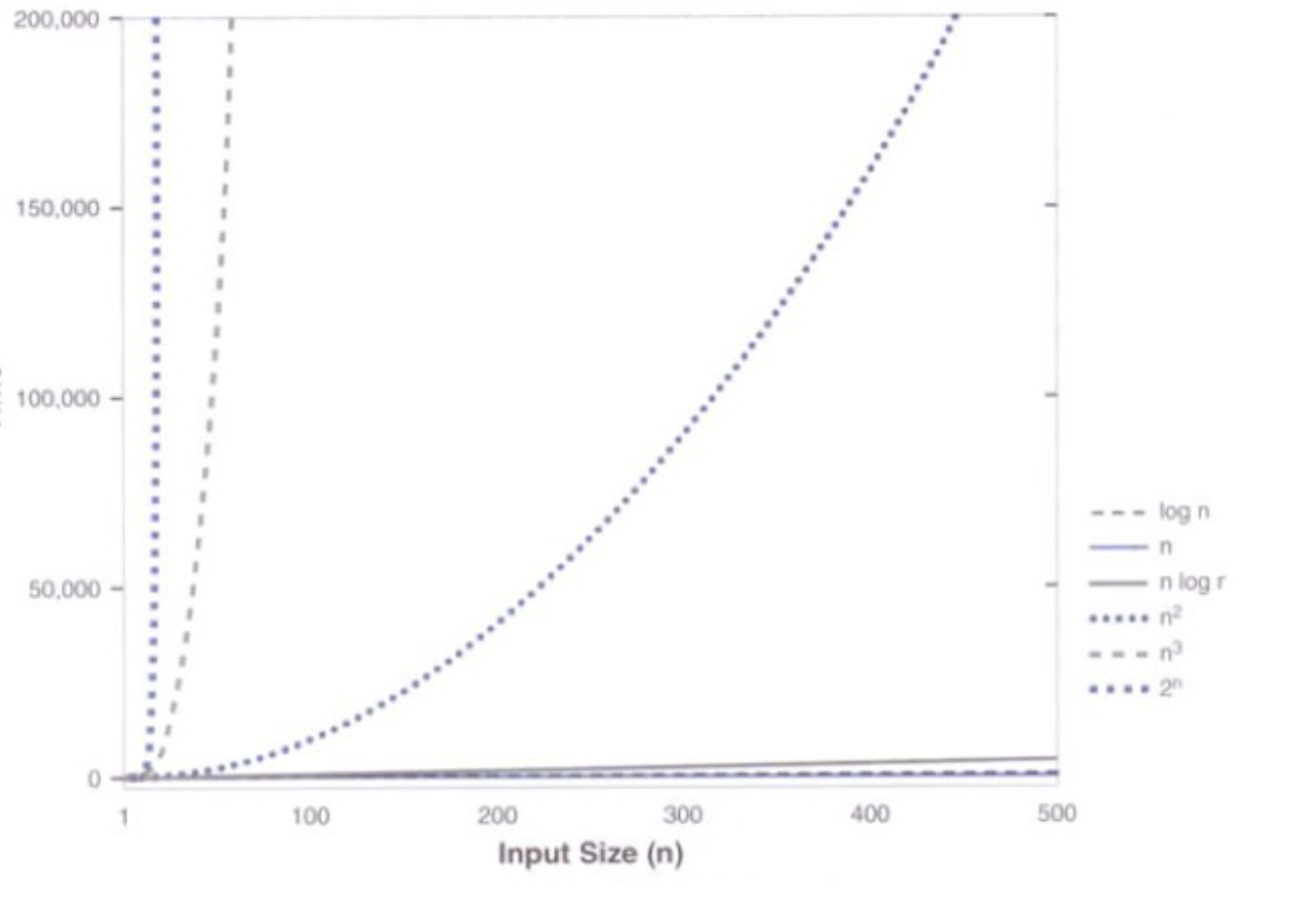
四、时间复杂度分析（重点）

1.要分析循环运行，首先要确定该循环体的阶次n，然后用该循环需要运行的次数乘它。

例：时间复杂度为O(n)的例子

for(int count = 0;count<n;count++)
{
//*复杂度为O(1)的步骤系列
}

例：如果循环的复杂程度是对数级的(时间复杂度为O(log n)

count = 1;
while(count < n)
{
count *=2;
//复杂度为O(1)的步骤系列
}

2.嵌套循环的复杂度分析

例：时间复杂度为O(n^2)

for(int count = 0;count < n;count++)
{
   for(int count2 = 0;count2<n;count2++)
    {
        //复杂度为O(1)的步骤系列
    }
}

3.方法调用的复杂度分析

例：时间复杂度为O(n^2)

for(int count = 0;count<n;count++)
{
    printsum(count);
}

public void printsum(int count)
{
    int sum = 0;
    for(int I = 1;I<count;I++)
        sum += I;
    System.out.println(sum);
}

五、时间复杂度的计算规律（重点）

设程序段和程序段2的时间分别为T1(n)和T2(n)，总的运行时间为T(n)

1.加法准则：T(n,m)=T1(n)+T2(n)

2.乘法准则：T(n)=T1(n)*T2(n)

3.特例情形：算法平均时间复杂度，算法最坏情况下的时间复杂度。

教材学习中的问题和解决过程

• 问题1:会不会存在一个方法调用的复杂度为O(1)的情况，是否可以理解为数学的先进行n次方，然后再开n次方根？
  
  比如举个例子：是否如下的代码的时间复杂度为O(1)

for(int count = 0;count<n;count++)
{
    {
        for(j=1;j<=count;j++)
            {
                printsum(count);
            }
       }
}

public void printsum(int count)
{
    int a=0;
   while(a^2<=count)
       a++;
}

• 问题1解决过程：
  
  以书本里的解答，我认为是可以这样认为的，因为它本身就是一个计算机问题演变出的数学问题，时间复杂度也就是循环的次数，同样，次数多计算法就是通过一系列计算所得到的，而问题中的计算只是一种对于对计算机问题的一种解释的手段，所以我觉得完全可以这样理解。

• 问题2：书本中总是出现没有底数的对数函数，那没有底数会不会算错呢？在什么时候该写底数呢？

• 问题2解答：
  
  经过查找资料，我找到这样一篇文章，可以有助于我们理解数据结构在这一方面的知识，资料叫做“剑指Offer——算法复杂度中的O(logN)底数是多少”，具体文章我已放在参考资料中，有兴趣的同学可以看看，我这里拿重点。
  
  

教材布置习题解答

EX 2.1 下列增长函数的阶次是多少？

a.10n^2+100n+1000

解答：因为渐进复杂度称为算法的阶次，因此该增长函数的阶次为：O(n^2)。

b.10n^3-7

解答：因为n^{3的增长速度最快，所以阶次为：O(n}3)

c.2ⁿ⁺¹⁰⁰ⁿ3

解答：因为n^3比2n增长速度慢，所以阶次为：O(2^n)

注：



d.n^2 ·log(n)

解答：阶次：O(n^2 ·log(n))

EX 2.4 请确定下面代码段的增长函数和阶次

for(int count = 0 ; count < n ; count++)
    for(int count2 = 0 ; count2 < n ; count2 = count2 + 2)
        {
            System.out.println(count,count2);
        }
}

解答：

• 增长函数为：F(n)=(n^2)/2
• 阶次为：O(n^2)
  
  解：因为内循环需要进行的次数是n/2，外循环需要进行的次数是n，因此，由老师上课所讲的乘法原理（T(n)=T1(n)*T2(n))可得，增长函数为：F(n)=(n^{2)/2；又因为阶数与增长函数的最高阶项有关，所以忽略次项与常数项。所以阶次为O(n}2)。

EX 2.5 请确定下面代码段的增长函数和阶次

for(int count = 0 ; count < n ; count++)
    for(int count2 = 0 ; count2 < n ; count2 = count2 * 2)
        {
            System.out.println(count,count2);
        }
}

解答：

• 增长函数：F(n)=n·log2(n)
• 阶次为：O(n·log2(n))
  
  解：因为外循环需要的次数为n次，内循环的次数是log2(n)，所以由乘法原理（T(n)=T1(n)*T2(n))可得，增长函数为：F(n)=n·log2(n)；又因为阶数与增长函数的最高阶项有关，所以忽略次项与常数项。所以阶次为O(n·log2(n))。

结对及互评

• 本周结对学习情况
  • 20172316赵乾宸
• 博客中值得学习的或问题：
  • 内容详略得当；
  • 代码调试环节比较详细；
• 基于评分标准，我给本博客打分：5分。得分情况如下：

1. 正确使用Markdown语法（加1分）：

2. 模板中的要素齐全（加1分）

3. 教材学习中的问题和解决过程, 一个问题加1分

4. 代码调试中的问题和解决过程, 一个问题加1分

   • 20172316唐才铭

• 博客中值得学习的或问题：
  • 内容详略得当；
  • 代码调试环节比较详细；
• 基于评分标准，我给本博客打分：9分。得分情况如下：

1. 正确使用Markdown语法（加1分）：
2. 模板中的要素齐全（加1分）
3. 教材学习中的问题和解决过程, 一个问题加1分
4. 代码调试中的问题和解决过程, 一个问题加1分

感悟

呀，新学期又到啦，我们又要学习啦，好开心呀哈哈哈。虽然感觉听起来有点假，的确，有点假，但是开学还是很开心的，可以和同学们一起玩，很开心的玩啊！然后又可以好好学习了，在家里感觉天天都在打游戏，不想学习，希望自己在新的一学期可以继续努力，认真学习，没有晚自习，自己要给自己晚自习的时间进行学习，希望自己可以学到更多有用的东西让自己以后的生活更好，养得起自己！

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）
目标	5000行	30篇	400小时
第一周	0/0	1/1	6/6

参考资料

蓝墨云班课

Java程序设计

算法运行时间1、logN、N、NlogN 、N^2、N3、2^n之间的比较

剑指Offer——算法复杂度中的O(logN)底数是多少