2018HN多校
http://acm.hi-54.com/contest_problemset.php?cid=1455
A : 摩斯密码
Progress Bar
时间限制:1 Sec 内存限制:128 MiB
提交:202 答案正确:82
题目描述
题目描述：
摩尔斯电码（又译为摩斯密码，Morse code）是一种时通时断的信号代码，通过不同的排列顺序来表达不同的英文字母、数字和标点符号。为了简单问题，去除所有的标点符号。
现在给你一段摩斯密码，请你把它们进行解密。
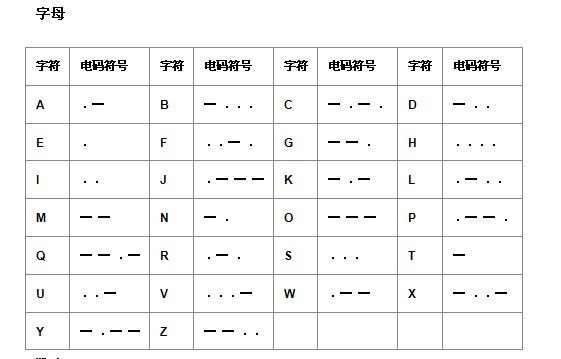
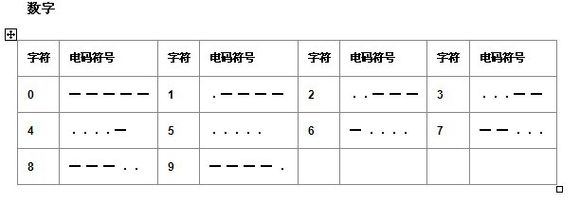
输入
含有T(T<=20)组数据，每组数据包含一段摩斯密码(由字符 '.' 和 '-' 以及 空格组成,连续空格个数不超过两个)，每段占一行(不超过1000个字符)，现在请你对他们进行解密；
输出
输出对应的解密后的结果(所有解密结果如果是英文字母一律输出小写英文字母)，保证结果仅包含 数字 空格 字母。
样例输入
复制
5
..
. .
. ..
. ..
.. .-.. --- ...- . -.-- --- ..-
样例输出
复制
i
ee
ei
e i
i love you map跑一发，但不知道为啥格式错误最后随便改了改A了。
#include<iostream>
#include<cstring>
#include<queue>
#include<cstdio>
#include<stack>
#include<set>
#include<map>
#include<cmath>
#include<ctime>
#include<time.h>
#include<algorithm>
#include<bits/stdc++.h>
using namespace std;
#define mp make_pair
#define pb push_back
#define debug puts("debug")
#define LL unsigned long long
#define pii pair<int,int>
#define eps 1e-10
#define inf 0x3f3f3f3f map<string,char>M;
void init(){
M[".-"]='a';M["-..."]='b';M["-.-."]='c';M["-.."]='d';
M["."]='e';M["..-."]='f';M["--."]='g';M["...."]='h';
M[".."]='i';M[".---"]='j';M["-.-"]='k';M[".-.."]='l';
M["--"]='m';M["-."]='n';M["---"]='o';M[".--."]='p';
M["--.-"]='q';M[".-."]='r';M["..."]='s';M["-"]='t';
M["..-"]='u';M["...-"]='v';M[".--"]='w';M["-..-"]='x';
M["-.--"]='y';M["--.."]='z';
M["-----"]='';M[".----"]='';M["..---"]='';M["...--"]='';
M["....-"]='';M["....."]='';M["-...."]='';M["--..."]='';
M["---.."]='';M["----."]='';
}
char s[];
int main()
{
LL n,m,i,j,k,t;
init();
cin>>t;
getchar();
while(t--){
string ans="";
string tmp="";
gets(s);
LL l=strlen(s);
for(i=;i<l;++i){
if(s[i]==' '){
ans+=M[tmp];
tmp="";
if(s[i+]==' '){
i++;
ans+=' ';
}
}
else{
tmp+=s[i];
}
}
ans+=M[tmp];
for(int i=;i<ans.length();++i){
if(isalpha(ans[i])){
ans[i]=tolower(ans[i]);
}
}
cout<<ans<<endl;
}
return ;
}
题目描述
有一个N x M 大小的地图，地图中的每个单元包含一个大写字母。
若两个相邻的(这里的相邻指“上下左右”相邻)点上的字母相同，我们可以用线段连接这两个点。
若存在一个包含同一字母的环路，那么连接这些点我们可以得到一个多边形，
当且仅当多边形的边数大于等于4时，我们称这幅地图中存在“简单环路”。
现在给你一份地图，你来判断是否存在“简单环路”。
列如：
3 4
AAAA
ABCA
AAAA
字符“A”可以构成一个“简单环路”，其边数为4。
输入
第一行输入两个正整数n,m，2<=n,m<=50，分别表示地图的行列数。
接下来输入n行，每行m个大写字母。
输出
若存在“简单环路”输出“Yes”，否则输出“No”。
样例输入
复制
3 4
AAAA
ABCA
AADA
样例输出
复制
No
判断一个图中是否有环，刚开始想的用dfs感觉写起来很麻烦，最后用的并查集，每个格子看作一个点，注意一条边并一次就好，
发现两个同类点在一个集合中说明有环。
#include<iostream>
#include<cstring>
#include<queue>
#include<cstdio>
#include<stack>
#include<set>
#include<map>
#include<cmath>
#include<ctime>
#include<time.h>
#include<algorithm>
#include<bits/stdc++.h>
using namespace std;
#define mp make_pair
#define pb push_back
#define debug puts("debug")
#define LL unsigned long long
#define pii pair<int,int>
#define eps 1e-10
#define inf 0x3f3f3f3f
LL MOD=1e9+; char s[][];
int e[][]; int f[];
int getf(int v){
return f[v]==v?v:f[v]=getf(f[v]);
}
LL t,n,m,i,j,k;
struct Edge{
int u,v,w;
}P[];
int gid(int x,int y){
return (x-)*m+y;
}
int main()
{ while(cin>>n>>m){
memset(e,,sizeof(e));
for(i=;i<=n*m;++i) f[i]=i;
for(i=;i<=n;++i) cin>>s[i]+;
bool ok=;
for(i=;i<=n;++i){
for(j=;j<=m;++j){
if(s[i][j]==s[i][j-]){
int u=gid(i,j),v=gid(i,j-);
int fu=getf(u),fv=getf(v);
if(fu!=fv){
f[fv]=fu;
}
else{
ok=;
break;
}
}
if(s[i][j]==s[i-][j]){
int u=gid(i,j),v=gid(i-,j);
int fu=getf(u),fv=getf(v);
if(fu!=fv){
f[fv]=fu;
}
else{//cout<<i<<' '<<j<<" "<<fu<<" "<<fv<<endl;
ok=;
break;
}
}
if(ok) break;
}
if(ok) break;
}
ok?puts("Yes"):puts("No");
}
return ;
} /*
.. .-.. --- ...- . -.-- --- ..---
*/
C直接模拟。
题目描述
题意简单到令人发指！
序列A由N个整数组成，从中选出一个连续的子序列，使得这个子序列的和为正数，且和为所有和大于零的子序列中的最小值.
将这个值输出，若无解，输出no solution。
输入
第一行输入一个正整数N（2<N<50000）<n<50000）<n<50000）<n<50000）< div="">
第二行输入N个整数
输出
输出最小的正子段和
样例输入
复制
3
-1 2 3
样例输出
复制
1
贪心，考虑一下这段序列的和 sum[i,j]=SUM{a[i]+a[i+1]+...+a[j]},我们的目标是 MIN{sum[i,j]},也可以改写成MIN{pre[j]-pre[i-1]},转化成了前缀和的形式，问题转化为找到两个前缀和pre[a]和pre[b]满足 a<b且pre[a]<pre[b] 的最小的pre[b]-pre[a],对处理好的pre[]数组排序，枚举右边界i,如果i-1满足条件那显然i-1就是当前最优的，如果i-1不满足条件，在i-1前面有满足条件的k，那么让i-1和k配对会使得结果更优，所以我们只考虑相邻的点就可以了。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define LL long long
pair<LL,int>sum[];
int a[];
int main()
{
int n,i,j;
cin>>n;
LL ans=;
for(i=;i<=n;i++) cin>>a[i];
for(i=;i<=n;i++) {
sum[i].first=sum[i-].first+a[i];
sum[i].second=i;
}
sort(sum+,sum++n);
if(sum[].first>)ans=sum[].first;
for(i=;i<=n;i++) {
if(sum[i].first>) ans=min(ans,sum[i].first);
if(sum[i].second>sum[i-].second && sum[i].first!=sum[i-].first) ans=min(ans,sum[i].first-sum[i-].first);
}
if(ans!=) cout<<ans<<endl;
else puts("no solution");
return ;
}
题目描述
广寒宫下有株二叉树，树上共有n个节点，通过n-1条树枝连接，树下有一只玉兔，吴刚提着斧子站在一旁。
他恼恨一切同他争夺嫦娥的事物，所以他决定通过砍二叉树上的n-1条树枝来毁掉这颗二叉树。
妙的是，这些树枝只能被砍一次，而且被砍后有一半的概率立即长出。
吴刚砍了n斧子后罢手了，他打算“不眠倚桂树”。你来猜猜，现在这株二叉树有多少联通块？（即联通块的期望值）
已知：最后一斧子砍了玉兔。
输入
输入一个正整数T（1<=T<=50）
接下来T行，每行输入一个正整数n，代表二叉树的节点数，2<=n<=1e5。
输出
输出联通块的期望值，答案的数据可能很大，所以输出答案乘2^(n-1)后再对1e9+7取模
样例输入
复制
1
2
样例输出
复制
3
提示
来源
直接根据题意列出来联通快个数分布律图，答案就是 { Σni=1(i*C(n-1,i-1)) }%1e9+7,由于组合数推到用到了除法需要取逆元，这里n不是很大，直接线性推导，inv[i]=(mod-mod/i)*inv[mod%i]%mod;记得中间取模防爆。
#include<iostream>
#include<cstring>
#include<queue>
#include<cstdio>
#include<stack>
#include<set>
#include<map>
#include<cmath>
#include<ctime>
#include<time.h>
#include<algorithm>
#include<bits/stdc++.h>
using namespace std;
#define mp make_pair
#define pb push_back
#define debug puts("debug")
#define LL unsigned long long
#define pii pair<int,int>
#define eps 1e-10
#define inf 0x3f3f3f3f
LL MOD=1e9+;
LL inv[]={,};
int main()
{
LL t,n,m,i,j,k;
for(i=;i<;++i)
inv[i]=(MOD-MOD/i)*inv[MOD%i]%MOD;
scanf("%lld",&t);
while(t--){
scanf("%lld",&n);
LL ans=;
LL r=;
for(i=;i<n;++i){
r=r*(n-i)%MOD*inv[i]%MOD;
ans+=(i+)*r;
ans%=MOD;
}
cout<<ans<<endl;
}
return ;
}
题目描述
我们把f(i)表示为i的正约数的和，而我们要求的是1<=i<=n之间所有i的f（i）之和！
输入
先输入一个正整数T，表示T个这是数据。T（T<=50）
每行输入一个正整数n。(n<10^6)
输出
输出一个数字，表示所求的数。
样例输入
复制
3
5
12
2018
样例输出
复制
21
127
3350309
1--n中因子x的个数就是floor(n/i);
#include<iostream>
#include<cstring>
#include<queue>
#include<cstdio>
#include<stack>
#include<set>
#include<map>
#include<cmath>
#include<ctime>
#include<time.h>
#include<algorithm>
#include<bits/stdc++.h>
using namespace std;
#define mp make_pair
#define pb push_back
#define debug puts("debug")
#define LL unsigned long long
#define pii pair<int,int>
#define eps 1e-10
#define inf 0x3f3f3f3f
LL MOD=1e9+; LL cal(int n){
LL r=n;
for(int i=;i<=n;++i){
r+=(n/i)*i;
}
return r;
}
int main(){
int n,i,j,k;
cin>>k;
while(k--){
scanf("%d",&n);
printf("%lld\n",cal(n));
}
return ;
}
题目描述
伴随着科技的发展，我们的生活也越来越多姿多彩，随着手机的普及，各种交友软件也在快速的发展。
小a是个老实人，当然只是自己理解而已，其实小a是个不折不扣的渣男。因为他在有女朋友的同时，还在疯狂的撒网，利用各种交友软件寻求更适合自己的伴侣。
小a女朋友当然不是省油的灯，自然了解小a的本性，所以在每次见面时就会翻看小a的软件记录，来了解小a近期的状况，机智的小a当然会在女朋友来之前就给完全清理干净了。
终于在某次时间紧急的情况下，小a的软件记录并不一定能够完全删除，但是小a知道，自己每个软件记录的火热程度以及最终删除时间（即可以删除的最晚时间，过时将无法删除）。每个软件记录的删除需要一分钟，软件记录的火热程度，正好对应着女朋友的刺激值，小a想知道，在有限的时间内，如何才能够让女朋友的刺激值最小，求出最小值。
输入
第一行一个正整数T。表示样例个数（0<T<10）
每组有两个整数n，m，分别表示一共有n个软件以及女朋友到来的时间（0<n<=10^5,0<m<=10^6）
往下对应着n行，每行有两个正整数e,f分别对应每个软件记录的火热程度和该软件的最终删除时间。(0<e<=10^5,0<f<=10^6)
题目中涉及到的时间全部以分钟为单位。
输出
输出对女朋友的最小刺激值；结果占一行。
样例输入
复制
2
4 2
20 1
10 1
30 2
40 2
6 2
20 1
10 1
30 2
40 2
50 3
60 3
样例输出
复制
30
100 贪心，考虑每个时间x，在这个时间点能销毁的软件的时间属性必须>=x,大的时间肯定不会影响小时间，倒序往堆里push节点每次pop队首就好了。
#include<iostream>
#include<cstring>
#include<queue>
#include<cstdio>
#include<stack>
#include<set>
#include<map>
#include<cmath>
#include<ctime>
#include<time.h>
#include<algorithm>
#include<bits/stdc++.h>
using namespace std;
#define mp make_pair
#define pb push_back
#define debug puts("debug")
#define LL unsigned long long
#define pii pair<int,int>
#define eps 1e-10
#define inf 0x3f3f3f3f
LL MOD=1e9+; struct node{
int a,b;
bool operator<(const node& tmp)const{
return a<tmp.a;
}
}P[];
bool cmpb(node A,node B){
return A.b>B.b;
}
priority_queue<node>q;
int main()
{
LL t,n,m,i,j,k;
cin>>t;
while(t--){
while(!q.empty()) q.pop();
scanf("%lld%lld",&n,&m);
LL sum=,ans=;
for(i=;i<=n;++i){
scanf("%d%d",&P[i].a,&P[i].b);
sum+=P[i].a;
}
sort(P+,P++n,cmpb);
for(i=m,j=;i>=;--i){
while(j<=n&&P[j].b>=i)
q.push(P[j++]);
if(!q.empty()){
ans+=q.top().a;
q.pop();
}
}
cout<<sum-ans<<endl;
}
return ;
}
H-dp+矩阵幂
原题bzoj1009,只不过这道题限制了可以转移的字母状态
#include<iostream>
#include<cstring>
#include<queue>
#include<cstdio>
#include<stack>
#include<set>
#include<map>
#include<cmath>
#include<ctime>
#include<time.h>
#include<algorithm>
#include<bits/stdc++.h>
using namespace std;
#define mp make_pair
#define pb push_back
#define debug puts("debug")
#define LL long long
#define ULL unsigned long long
#define uint unsigned int
#define pii pair<int,int>
#define eps 1e-10
#define inf 0x3f3f3f3f char s1[],s2[];
LL mod=(LL)<<;
struct matrix{
int len;
LL a[][];
matrix(){
memset(a,,sizeof(a));
}
matrix operator*(matrix& tmp){
matrix ans;
ans.len=len;
for(int i=;i<=len;++i){
for(int j=;j<=len;++j){
for(int k=;k<=len;++k){
ans.a[i][k]+=a[i][j]*tmp.a[j][k];
ans.a[i][k]%=mod;
}
}
}
return ans;
} void show(){
puts("------------------------------------");
for(int i=;i<=len;++i){
for(int j=;j<=len;++j){
cout<<a[i][j]<<' ';
}
cout<<endl;
}
puts("------------------------------------");
}
}A,I;
matrix qpow(matrix X,int n){
matrix ans=I;
while(n){
if(n&) ans=ans*X;
X=X*X;
n>>=;
}
return ans;
}
int t,n,m,i,j,k;
int f[];
void solve(){
int l1=strlen(s1+),l2=strlen(s2+);
A.len=I.len=l2;
memset(A.a,,sizeof(A.a));
for(i=;i<=l2;++i) I.a[i][i]=;
f[]=,f[]=;
for(i=;i<=l2;++i){
j=f[i-];
while(j&&s2[j]!=s2[i-]) j=f[j];
f[i]=j+;
}
for(i=;i<l2;++i){
for(j=;j<=l1;++j){
k=i+;
while(k&&s1[j]!=s2[k]) k=f[k];
A.a[i][k]++;
A.a[i][k]%=mod;
}
} A.a[l2-][l2]=;
//A.show();
matrix ans=qpow(A,n);
LL res=;
for(i=;i<l2;++i) res=(res+ans.a[][i])%mod;
cout<<res<<endl;
}
int main(){ scanf("%d",&t);
while(t--){
scanf("%d%s%s",&n,s1+,s2+);
solve();
}
return ;
}
/*
3
3
ab
ab
4
acd
ca 5
ab
aaa
*/
I，b-a;
题目描述
每个人 都有自己独有的计数方式 比如以下 字符串111123455可以表示为4个1,1个2,1个3，1个4,2个5.为了方便记忆就表示为4--1,1--2,1--3,1--4,2--5当然顺序肯定不能变换 计数方式可以表示为“a--b”的形式 在计数方式中相连的b互不相等且a与b不为0 独有的计数方式 如果转化为字符串 字符串的长度小于10的9次方
给你下面的计数方式 例如5--4也就是字符串44444，10--4也就是字符串4444444444
给你这样的计数方式 判断这个字符串中有多少连续子串所构成的整数是4的倍数
例如5--4可表示为字符串44444里面共有（4,4,4,4,4,44,44,44,44,444,444,444,4444,4444,44444）15个是4的倍数;
输入
第一行是数字T（T<1000)<t<100） 表示下面有t组实例<="" h3="">
每一行一个独有的计数方式 长度小于100
<t<100） 表示下面有t组实例<="" h3="">
输出
输出字符串中有多少个是4的倍数 占一行
样例输入
复制
4
5--4
1--1,1--2
2--4,2--2,2--3
1--4,1--3,1--2,1--1
样例输出
33
打表查一下4的倍数的数字会发现规律，对于个位数，只有4/8是4的倍数，对于多位数，如果个位是奇数那他不可能是4的倍数，
如果
个位数是0/4/8,那十位数只有是偶数，这个数才是4的倍数；如果个位数是2/6那么十位数只有是奇数这个数才是4的倍数。
知道规律就简单了，记录下pre表示前面几段有多少个数字，枚举一下当前段的数字，奇数不管，2/6就加上pre，4/8根据前面的
数的奇偶性分情况讨论一下。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define LL long long
#define uint unsigned int LL a[],b[];
char s[];
int main()
{
int i,j,k,t; scanf("%d",&t);
getchar();
while(t--){
int tot=;
gets(s);
LL ans=,pre=; LL n=strlen(s),tmp=;
s[n]=',';
for(i=;i<=n;++i){
if(isdigit(s[i])){
tmp=tmp*+(s[i]-'');
}
else if(s[i]=='-'){
i++;
tot++;
a[tot]=tmp;
tmp=;
}
else if(s[i]==','){
b[tot]=tmp;
tmp=;
}
}
for(i=;i<=tot;++i){ if(b[i]==||b[i]==){
if(b[i-]%==){
ans+=pre;
}
}
else if(b[i]==||b[i]==){
if(b[i-]%==){
ans+=a[i]*(pre+pre+a[i]+)/;
}
else{
ans+=a[i]*(pre+pre+a[i]+)/;
ans=ans-pre;
}
}
pre+=a[i];
}
cout<<ans<<endl;
}
return ;
}
2018HN多校的更多相关文章
- 【开源毕设】一款精美的家校互动APP分享——爱吖校推 [你关注的，我们才推]（持续开源更新3）附高效动态压缩Bitmap
一.写在前面 爱吖校推如同它的名字一样,是一款校园类信息推送交流平台,这么多的家校互动类软件,你选择了我,这是我的幸运.从第一次在博客园上写博客到现在,我一次一次地提高博文的质量和代码的可读性,都是为 ...
- 2016 华南师大ACM校赛 SCNUCPC 非官方题解
我要举报本次校赛出题人的消极出题!!! 官方题解请戳:http://3.scnuacm2015.sinaapp.com/?p=89(其实就是一堆代码没有题解) A. 树链剖分数据结构板题 题目大意:我 ...
- NTP校时设置
一.Windows Server 2008 – Time Server 前言: 国家时间与频率标准实验室 && NTP服务器 也可以忽略1~6 直接跳7 如果已改过机码请使用 1 ...
- 2016暑假多校联合---Rikka with Sequence (线段树)
2016暑假多校联合---Rikka with Sequence (线段树) Problem Description As we know, Rikka is poor at math. Yuta i ...
- 2016暑假多校联合---Windows 10
2016暑假多校联合---Windows 10(HDU:5802) Problem Description Long long ago, there was an old monk living on ...
- 2016暑假多校联合---Substring（后缀数组）
2016暑假多校联合---Substring Problem Description ?? is practicing his program skill, and now he is given a ...
- 2016暑假多校联合---To My Girlfriend
2016暑假多校联合---To My Girlfriend Problem Description Dear Guo I never forget the moment I met with you. ...
- 2016暑假多校联合---A Simple Chess
2016暑假多校联合---A Simple Chess Problem Description There is a n×m board, a chess want to go to the po ...
- HDU 5792---2016暑假多校联合---World is Exploding
2016暑假多校联合---World is Exploding Problem Description Given a sequence A with length n,count how many ...
随机推荐
- PL/SQL编程基础(一)：PL/SQL语法简介（匿名PL/SQL块）
PL/SQL PL/SQL是Oracle在关系数据库结构化查询语言SQL基础上扩展得到的一种过程化查询语言. SQL与编程语言之间的不同在于,SQL没有变量,SQL没有流程控制(分支,循环).而PL/ ...
- 详解spring boot mybatis全注解化
本文重点介绍spring boot mybatis 注解化的实例代码 1.pom.xml //引入mybatis <dependency> <groupId>org.mybat ...
- 修改mysql的字符集和默认存储引擎
转自:http://blog.csdn.net/wyzxg/article/details/8779682 author:skatetime:2012/05/18 修改mysql的字符集和默认存储引擎 ...
- 纯css3加载动画
<!DOCTYPE html><html> <head> <meta charset="utf-8"> <meta name= ...
- mysql float 浮点型
定点数类型 DEC等同于DECIMAL 浮点类型:FLOAT DOUBLE 作用:存储薪资.身高.体重.体质参数等 m,d 都是设置宽度 =============================== ...
- pyenv常用命令
pyenv使用教程 安装 Mac brew install pyenv brew install pyenv-virtualenv 配置 echo 'eval "$(pyenv init - ...
- Linux系统——FTP
FTP连接及传输模式1. 控制连接:TCP21,用于发送FTP命令信息2. 数据连接:TCP20,用于上传.下载数据3. 数据连接的建立类型:(1)主动模式:服务器制动发起数据连接首先由客户端向服务端 ...
- 获取用户真实Ip地址
REMOTE_ADDR 是你的客户端跟你的服务器“握手”时候的IP.如果使用了“匿名代理”,REMOTE_ADDR将显示代理服务器的IP.HTTP_CLIENT_IP 是代理服务器发送的HTTP头.如 ...
- 198. House Robber(动态规划)
198. House Robber You are a professional robber planning to rob houses along a street. Each house ha ...
- Codeforces Round #523 (Div. 2) Solution
A. Coins Water. #include <bits/stdc++.h> using namespace std; int n, s; int main() { while (sc ...