【学时总结】◆学时·VIII◆ 树形DP

◆学时·VIII◆ 树形DP

DP像猴子一样爬上了树……QwQ

---

◇ 算法概述

基于树的模型，由于树上没有环，满足DP的无后效性，可以充分发挥其强大统计以及计算答案的能力。

一般来说树形DP的状态定义有三种：偏简单的，dp[u]表示以u为根的子树的最优解/方案数；带选择性质的：dp[u][0/1]，表示以u为根的子树中选择/不选择u的最优解/方案数；dp[u][i] 表示以u为根的子树中，u的状态为i的最优解/方案数（其实就是第二种定义的扩展）。

一般来说题目给的是一个树形图，那么我们只需要从图中一个存在的节点开始DP即可。注意向下DP时不要重复访问父节点。

由于树这种结构中，儿子与父亲的关系比较紧密，我们一般采用记忆化搜索，可以减免大量不合法的计算（只有儿子与父亲之间才能直接计算）。

---

◇ 经典选讲

（均出自《算法竞赛入门经典》-刘汝佳）

【UVa 12186】Another Crisis（工人的请愿书）

<题意>

某公司里有一个老板和n（n≤10 5 ）个员工组成树状结构，除了老板之外每个员工都有唯一的直属上司。老板的编号为0，员工编号为1～n。工人们（即没有直接下属的员工）打算签署一项请愿书递给老板，但是不能跨级递，只能递给直属上司。当一个中级员工（不是工人的员工）的直属下属中不小于T%的人签字时，他也会签字并且递给他的直属上司。问：要让公司老板收到请愿书，至少需要多少个工人签字？

<解析>

这道题实质上是给定了一个以老板为根的有根树，于是我们DP的起点便是老板。定义状态为dp[u]为员工u签字最少需要多少个人签字。

对于工人u（没有直接下属），能够直接提供一个签字，即dp[u]=1，仅需要一人签字。对于其他非工人员工v，我们计算出他的每一个直属下属的dp值，存入cnt；再通过题目提供的百分数，算出要让他签字，他的直属下属员工最少有多少个需要签字，记为Maxi；那么要让v签字，最少要签字的人数为cnt中前Maxi个最小的值之和。

因为我们要使答案尽量小，取前Maxi个最小的值就可以达到目的。

（详见代码，如果有一些没懂的可以在邮箱里询问~）

<源代码>

 /*Lucky_Glass*/
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<vector>
 using namespace std;
 const int MAXN=int(1e5);
 vector<int> lnk[MAXN+];
 int n,m;
 int dp[MAXN+];
 inline bool cmp(int A,int B){return dp[A]<dp[B];}
 int DP(int u){
     if(dp[u]) return dp[u];
     if(lnk[u].size()==) return dp[u]=;
     vector<int> cnt;
     for(int i=;i<(int)lnk[u].size();i++)
         cnt.push_back(DP(lnk[u][i]));
     sort(cnt.begin(),cnt.end());
     int Maxi=lnk[u].size()*m/+(lnk[u].size()*m%? :);
     for(int i=;i<Maxi;i++)
         dp[u]+=cnt[i];
     return dp[u];
 }
 int main(){
     //freopen("in.txt","r",stdin);
     while(~scanf("%d%d",&n,&m) && n && m)
     {
         memset(dp,,sizeof dp);
         memset(lnk,,sizeof lnk);
         for(int i=,pre;i<=n;i++)
             scanf("%d",&pre),lnk[pre].push_back(i);
         printf("%d\n",DP());
     }
     return ;
 }

Another Crisis

【UVa 1220】Party at Hali-Bula（Hali-Bula的晚会）

<题意>

公司里有n（n≤200）个人形成一个树状结构，即除了老板之外每个员工都有唯一的直属上司。要求选尽量多的人，但不能同时选择一个人和他的直属上司。问：最多能选多少人，以及在人数最多的前提下方案是否唯一。输出第一个数为最多能选多少人，接下来若仅有一种选择方案能够达到最大选择人数，则输出Yes，否则输出No。

<解析>

本题相对上一题又多了一层状态——当前节点选或不选。也就是最开始在算法概述中描述的第二种状态定义。

先处理输入，我们先利用STL容器map<string,int>将名字映射到编号上，相当于重新编了号，固定“老板”的编号为1。

根据题意可知，对于一棵子树，若选取其根节点，则根节点的所有儿子都不能选；若不选根节点，则根节点的儿子可选可不选。那么我们DP开始时就要先判断“老板”这个节点选还是不选，即在dp[1][0]和dp[1][1]中取较大值。那么可以得到下面的状态转移方程式：

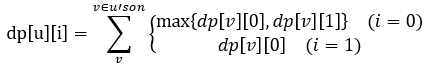
应该还是很好理解吧