数独问题的介绍及POJ 2676-Sudoku（dfs+剪枝）

知道是数独问题后犹豫了一下要不要做（好像很难的样纸==。），用dfs并剪枝，是一道挺规范的搜索题。

先介绍以下数独吧～

数独（Sudoku）是一种运用纸、笔进行演算的逻辑游戏。玩家需要根据9×9盘面上的已知数字，推理出所有剩余空格 的数字，并满足每一行、每一列、每一个粗线宫内的数字均含1-9，不重复。 每一道合格的数独谜题都有且仅有唯一答案，推理方法也以此为基础，任何无解或多解的题目都是不合格的。

有一种求解数独问题的方案是“候选数字法”，就是在待填充的格子中填写不会造成行重复、列重复、块重复的数字，有的时候存在多个这样的数字，那么我们可以随机选取一个，如果待填充的格子中填写任何一个数字都会造成某种重复的发生，则说明这个问题没有解，也就是这不是一个数独问题。

想要更加深入了解的同学可以点此链接：http://www.cnblogs.com/grenet/archive/2013/06/19/3138654.html

下面来说说POJ的这道题吧！

题目大意：

给你一个数独，让你填数：

1.每行的九个数字互不相同；

2.每列的九个数字各不相同；

3.被分成的3*3的小矩阵中的九个数字互不相同；

输出完成后的数表，若不能满足上述条件，则输出原图。

解题思路：

DFS。。失败了回溯～

从小优女神那里看到的存储方式（觉得很是方便呀！）

用三个数组进行标记每行、每列、每个子网格已用的数字，用于剪枝

bool row[10][10];    //row[i][x]  标记在第i行中数字x是否出现了

bool col[10][10];    //col[j][y]  标记在第j列中数字y是否出现了

bool small[10][10];   //small[k][x] 标记在第k个3*3子格中数字z是否出现了

row 和 col的标记比较好处理，关键是找出small子网格的序号与 行i列j的关系

即要知道第i行j列的数字是属于哪个子网格的

首先我们假设子网格的序号如下编排：

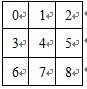
由于1<=i、j<=9，我们有： （其中“/”是C++中对整数的除法）

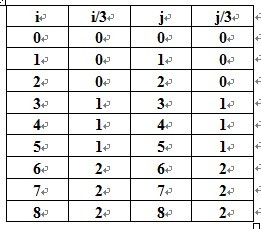
令a= i/3 , b= j/3  ，根据九宫格的 行列 与 子网格 的 关系，我们有:

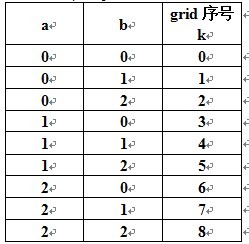
不难发现 3a+b=k

即 3*(i/3)+j/3=k

又我在程序中使用的数组下标为 1~9，grid编号也为1~9

因此上面的关系式可变形为 3*((i-1)/3)+(j-1)/3+1=k

这样我们就能记录k个3*3子格中数字z是否出现了：

下面是我的代码：

 #include<iostream>
 #include<cstdio>
 #include<ctime>
 #include<cstring>
 #include<cmath>
 #include<algorithm>
 #include<cstdlib>
 #include<vector>
 #define inf 1<<25
 #define LL long long
 using namespace std;
 int row[][];
 int col[][];
 int map[][];
 int small[][];
 int f(int x,int y)
 {
     return *((x-)/)+(y-)/+;
 }
 void init()
 {
     int i,j;
     char ch;
     memset(row,,sizeof(row));
     memset(col,,sizeof(col));
     memset(small,,sizeof(small));
     for(i=; i<=; i++)
         {
             for(j=; j<=; j++)
             {
                 scanf("%c",&ch);
                 map[i][j]=ch-'';
                 if(map[i][j])
                 {
                     int k;
                     k=f(i,j);
                     row[i][map[i][j]]=;
                     col[j][map[i][j]]=;
                     small[k][map[i][j]]=;
                 }
             }
             getchar();
         }
 }
 int dfs(int x,int y)
 {
     if(x==)
         return ;
     int flag=;
     if(map[x][y])
     {
         if(y==)
             flag=dfs(x+,);
         else
             flag=dfs(x,y+);
         if(flag)
             return ;
         else
             return ;
     }
     else
     {
         int k=f(x,y);
         for(int i=; i<=; i++)
             if(!row[x][i] && !col[y][i] && !small[k][i])
             {
                 map[x][y]=i;
                 row[x][i]=;
                 col[y][i]=;
                 small[k][i]=;
                 if(y==)
                     flag=dfs(x+,);
                 else
                     flag=dfs(x,y+);
                 if(!flag)
                 {
                     map[x][y]=;
                     row[x][i]=;
                     col[y][i]=;
                     small[k][i]=;
                 }
                 else
                     return ;
             }
     }
     return ;
 }
 int main()
 {
     int t;
     scanf("%d",&t);
     getchar();
     while(t--)
     {
         init();
         dfs(,);
         for(int i=; i<=; i++)
         {
             for(int j=; j<=; j++)
                 printf("%d",map[i][j]);
             printf("\n");
         }
     }
     return ;
 }