Mod in math

An Introduction to Modular Math

When we divide two integers we will have an equation that looks like the following:

AB=Q remainder R\dfrac{A}{B} = Q \text{ remainder } R​B​​A​​=Q remainder R

AAA
is the dividend

BBB
is the divisor

QQQ
is the quotient

RRR
is the remainder

Sometimes, we are only interested in what the remainder is when we divide
AAA
by BBB.

For these cases there is an operator called the modulo operator (abbreviated as mod).

Using the same AAA,
BBB,
QQQ,
and RRR
as above, we would have: A mod B=RA \text{ mod } B = RA mod B=R

We would say this as AAA
modulo BBB
is congruent to RRR.
Where BBB
is referred to as the modulus.

For example:

13513 mod 5==2 remainder 33

Visualize modulus with clocks

Observe what happens when we increment numbers by one and then divide them by 3.

03132333435363=======0 remainder 00 remainder 10 remainder 21 remainder 01 remainder 11 remainder 22 remainder 0

The remainders start at 0 and increases by 1 each time, until the number reaches one less than the number we are dividing by. After that, the sequence
repeats.

By noticing this, we can visualize the modulo operator by using circles.

We write 0 at the top of a circle and continuing clockwise writing integers 1, 2, ... up to one less than the modulus.

For example, a clock with the 12 replaced by a 0 would be the circle for a modulus of 12.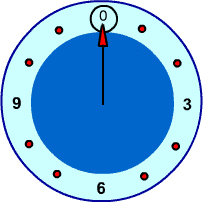

To find the result of A mod BA \text{ mod } BA mod B
we can follow these steps:

1. Construct this clock for size BBB
2. Start at 0 and move around the clock AAA
   steps
3. Wherever we land is our solution.

(If the number is positive we step clockwise, if it's negative we step
counter-clockwise.)

---

Examples

8 mod 4=?8 \text{ mod } 4 = ?8 mod 4=?

With a modulus of 4 we make a clock with numbers 0, 1, 2, 3.

We start at 0 and go through 8 numbers in a clockwise sequence 1, 2, 3, 0, 1, 2, 3, 0.

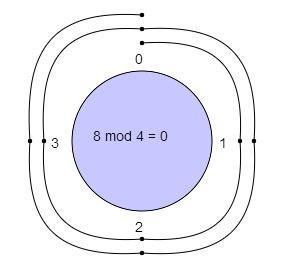
We ended up at 0 so 8 mod 4=0.

7 mod 2=?7 \text{ mod } 2 = ?7 mod 2=?

With a modulus of 2 we make a clock with numbers 0, 1.

We start at 0 and go through 7 numbers in a clockwise sequence 1, 0, 1, 0, 1, 0, 1.

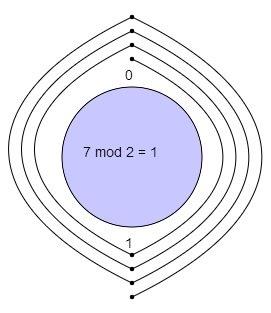
We ended up at 1 so 7 mod 2=1.

−5 mod 3=?-5 \text{ mod } 3 = ?−5 mod 3=?

With a modulus of 3 we we make a clock with numbers 0, 1, 2.

We start at 0 and go through 5 numbers in counter-clockwise sequence (5 is
negative) 2, 1, 0, 2, 1.

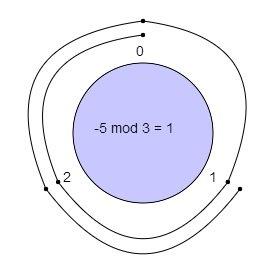
We ended up at 1 so −5 mod 3=1.

---

Conclusion

If we have A mod BA \text{ mod } BA mod B and
we increase AAA
by a multiple of B,
we will end up in the same spot, i.e.

A mod B=(A+K⋅B) mod BA \text{ mod } B = (A + K \cdot B) \text{ mod } BA mod B=(A+K⋅B) mod B for
any integer K.

For example:

3 mod 10=313 mod 10=323 mod 10=333 mod 10=3

Notes to the Reader

mod in programming languages and calculators

Many programming languages, and calculators, have a mod operator, typically represented with the % symbol. If you calculate the result of a negative number, some languages will give you a negative result.

e.g.

-5 % 3 = -2.In a future article we will explain, why this happens, and what it means.

Congruence Modulo

You may see an expression like:

A≡B (mod C)A \equiv B\ (\text{mod } C)A≡B (mod C)

This says that AAA
is congruent to BBB
modulo CCC.
It is similar to the expressions we used here, but not quite the same.

In the next article we will explain what it means and how it is related to the expressions above.