Golomb及指数哥伦布编码原理介绍及实现

2017年的第一篇博文。

本文主要有以下三部分内容：

• 介绍了Golomb编码，及其两个变种：Golomb-Rice和Exp-Golomb的基本原理
• C++实现了一个简单的BitStream库，能够方便在bit流和byte数字之间进行转换
• C++实现了Golomb-Rice和Exp-Golomb的编码，并进行了测试。

在文章的最后提供了本文中的源代码下载。

Golomb编码的基本原理

Golomb编码是一种无损的数据压缩方法，由数学家Solomon W.Golomb在1960年代发明。Golomb编码只能对非负整数进行编码，符号表中的符号出现的概率符合几何分布(Geometric Distribution)时，使用Golomb编码可以取得最优效果，也就是说Golomb编码比较适合小的数字比大的数字出现概率比较高的编码。它使用较短的码长编码较小的数字，较长的码长编码较大的数字。

Golomb编码是一种分组编码，需要一个正整数参数m，然后以m为单位对待编码的数字进行分组，如下图：

对于任一待编码的非负正整数N，Golomb编码将其分为两个部分：所在组的编号GroupID以及分组后余下的部分，GroupID实际是待编码数字N和参数m的商，余下的部分则是其商的余数，具体计算如下：

\[ \begin{array}{c}
q = N / m \\ \\
r = N \% m
\end{array}
\]

对于得到的组号q使用一元编码(Unary code)，余下部分r则使用固定长度的二进制编码(binary encoding)。

一元编码(Unary coding)是一种简单的只能对非负整数进行编码的方法，对于任意非负整数num，它的一元编码就是num个1后面紧跟着一个0。例如：

num	Unary coding
0	0
1	10
2	110
3	1110
4	11110
5	111110

其编解码的伪代码如下：

UnaryEncode(n) {
    while (n > 0) {
        WriteBit(1);
        n--;
    }
    WriteBit(0);
}

UnaryDecode() {
    n = 0;
    while (ReadBit(1) == 1) {
        n++;
    }
    return n;
}

使用一元编码编码组号也就是商q后，对于余下的部分r则有根据编码数字大小的不同有不同的处理方法。

• 如果参数m是2的次幂（这也是下面将要介绍的Golomb-Rice编码），则使用取r的二进制表示的低\(\log_2(m)\)位，作为r的码字
• 如果参数m不是2的次幂，如果m不是2的次幂，设\(b = \lceil{\log_2(m)}\rceil\)
  1. 如果\(r < 2^b - m\)，则使用b-1位的二进制编码r。
  2. 如果\(r \geqq 2^b -m\)，则使用b位二进制对\(r+2^b-m\)进行编码

总结，设待编码的非负整数为N，Golomb编码流程如下：

• 初始化正整数参数m
• 取得组号q以及余下部分r，计算公式为：\(q = N / m,r = N \% m\)
• 使用一元编码的方式编码q
• 使用二进制的方式编码r，r所使用位数的如下：
  • 如果参数m是2的次幂（这也是下面将要介绍的Golomb-Rice编码），则使用取r的二进制表示的低\(\log_2(m)\)位，作为r的码字。
  • 如果参数m不是2的次幂，如果m不是2的次幂，设\(b = \lceil{\log_2(m)}\rceil\)
    1. 如果\(r < 2^b - m\)，则使用b-1位的二进制编码r。
    2. 如果\(r \geqq 2^b -m\)，则使用b位二进制对\(r+2^b-m\)进行编码

说明：

• \(\lceil a \rceil\) 大于a的最小整数 ceil运算
• \(\lfloor a \rfloor\) 小于a的最大整数 floor运算

Golomb-Rice 编码

Golomb-Rice是Golomb编码的一个变种，它给Golomb编码的参数m添加了个限制条件：m必须是2的次幂。这样有两个好处：

• 不需要做模运算即可得到余数r，r = N & (m - 1)
• 对余数r编码更为简单，只需要取r二进制的低\(\log_2(m)\)位即可。

则Golomb-Rice的编码过程更为简洁：

• 初始化参数m，m必须为2的次幂
• 计算q和r，q = N / m ; r = N & (m - 1)
• 使用一元编码编码q
• 取r的二进制位的低\(\log_2(m)\)位作为r的码字。

解码过程如下：

bool b;
uint64_t unary = 0;
b = bitStream.getBit();
while (b)
{
    unary++;
    b = bitStream.getBit();
}

std::bitset<64> bits;
bits.reset();
for (int i = 0; i < k; i++)
{
    b = bitStream.getBit();
    bits.set(i, b);
}

N  = unary * m + bits.to_ulong();

Exponential Golomb 指数哥伦布编码

Rice的编码方式和Golomb的方法是大同小异的，只是选择m必须为2的次幂。而Exp-Golomb则有了一个很大的改进，不再使用固定大小的分组，而使组的大小呈指数增长。如下图：

Exp-Golomb的码元结构是：** [M zeros prefix] [1] [Offset] **，其中M是分组的编号GroupID，1可以看着是分隔符，Offset是组内的偏移量。

Exp-Golomb需要一个非负整数K作为参数，称之为K阶Exp-Golomb。其中当K = 0时，称为0阶Exp-Golomb，目前比较流行的H.264视频编码标准中使用的就是0阶的Exp-Golomb，并且可以将任意的阶数K转为0阶Exp-Golomb编码。

首先来看下0阶Exp-Golomb编码，如下图：

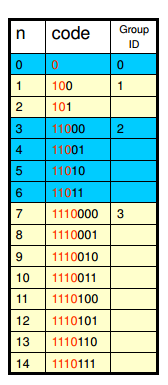
上图是0阶Exp-Golomb编码的前几个组的分组情况，可以看出编号为m的组，其组内的最小元素的值是\(2 ^ m - 1\)，也就是说对于非负整数N，其在编号为m的组内的充要条件是：\(2^m-1 \leq N \leq 2^{m+1}-1\)。所以可以由如下公式计算得到组号m以及组内的偏移量Offset

\[ \begin{array}{r}
m = \lfloor{log_2{(num+1)}}\rfloor \\
\\
Offset = num + 1 - 2^m
\end{array}
\]

有了组号以及组内的偏移量后，其编码就比较简单了，具体过程如下：

• 首先使用公式计算组号m，\(m = \lfloor{log_2{(num+1)}}\rfloor\)
• 对组号m进行编码，连续写入m个0，最后写入一个1作为结束。
• 计算组内偏移量offset,\(Offset = num + 1 - 2^m\)
• 取offset二进制形式的低m位作为offset码元

0阶Exp-Golomb的编码后的长度是：\(2*m + 1\)，其解码过程和上面的Rice码类似，读入bit流，是0则继续，1则停止，然后统计0的个数m；接着读入m位的bit，就是offset，最后解码后的数值是：\(N = 2^m - 1 + offset\)。

k阶Exp-Golomb

前面提到任意的k阶Exp-Golomb可以转换为0阶Exp-Golomb进行求解，这是为何呢。Exp-Golomb的组的大小实际上是呈2的指数增长，不同的参数k，实际控制的是起始分组的大小，具体是什么意思呢。

• k = 0,其组的大小为1，2，4，8，16，32，...
• k = 1,其组的大小为2，4，8，16，32，64，...
• k = 2,其组的大小为4，8，16，32，64，...
• ...
• k = n,其组的大小为\(2^n,2^{n+1},\cdots\)

不同的k造成了其起始分组的大小不同，所以对于任意的k阶Exp-Golomb编码都可以转化为0阶，具体如下：

设待编码数字为N，参数为k

• 使用0阶Exp-Golomb编码 \(N + 2^k - 1\)
• 从第一步的结果中删除掉高位的k个0

以上的算法描述来自： https://en.wikipedia.org/wiki/Exponential-Golomb_coding

在搜索得到中文资料中，对于K阶Exp-Golomb的算法描述大多如下：

• 将num以二进制的形式表示（若不足k位，则在高位补0）,去掉其低k位（若刚好是k位，则为0）得到数字n
• 计算n + 1的最低有效位数lsb，则M = lsb - 1。就是prefix中0的个数
• 将第1步中去掉的k位二进制串放到(n + 1)的低位，得到[1][INFO]

其实现以及描述都不如wikipedia，故在下面的实现部分使用的是Wikipedia的方法。

在资料搜集的过程中，对于Exp-Golomb算法描述不止上述的两种，还有其他的形式，但都是殊途同归，也许得到的编码是不一样的，但是其编码的长度却是一样的，也就没有过多的计较。

最后附上k = 0,1,2,3时前29个数字的编码:

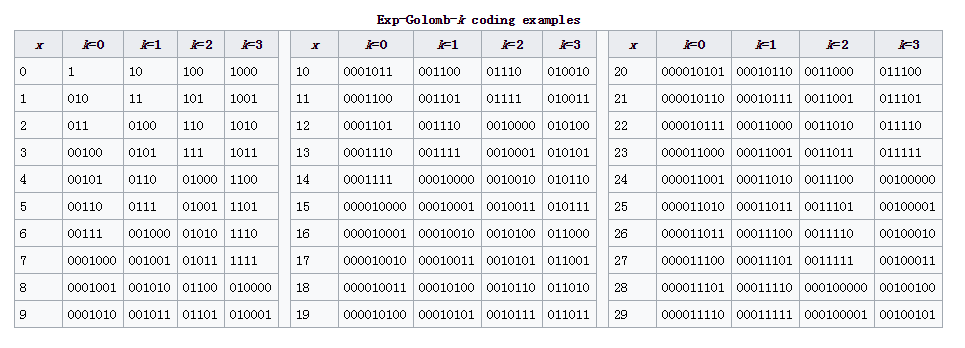
注意1之前的0的个数就是该数字所在的组的编号，同一组内的编码长度是相同的。

实现

通过上面的描述可以发现，Golomb编码的实现是很简单的，唯一的难点在于bit的操作。编码过程是将对bit进行操作，然后拼凑为byte，写入buffer；解码则是相反的过程，读取byte转化为bit stream，操作一个个的bit。具体来说就是以下两个功能：

• 将bit流转换为byte数组
• 将byte数组转换为bit流

而在C/C++中最小的数据类型也是8位的byte，这就造成了对bit的进行操作有一定的难度，好在C++中std::bitset结构能够在一定成都上简化对bit的操作。

BitBuffer / ByteBuffer

首先实现一个底层的库，实现bit流和byte之间的转换。在Golomb编码中，对bit和byte的操作只需要简单的get/put操作，因此封装了两个结构体BitBuffer和ByteBuffer，具体的声明如下：

//////////////////////////////////////////////////////
//
// Bits buffer
//	将bytes转化为bit stream时,在该buffer中缓存待处理的bit
//
/////////////////////////////////////////////////////
struct BitBuffer
{
	std::bitset<bit_length> data; // 使用bitset缓存bit
	int						pos;  // 当前bit的指针
	int						count;// bitset中bit的个数

	// 构造函数
	BitBuffer();

	// 从bitset中取出一个bit
	bool getBit();

	// 从bitset中取出一个byte
	uint8_t getByte();

	// 向bitset中写入一个bit
	void putBit(bool b);

	// 向bitset中写入一个byte
	void putByte(uint8_t b);
};

////////////////////////////////////////////////////
//
// Bytes buffer
//
///////////////////////////////////////////////////
struct ByteBuffer
{
	uint8_t *data;   // Byte数据指针
	uint64_t pos;    // 当期byte的指针
	uint64_t length; // 数据长度

	uint64_t totalLength; // 总的放入到 byte buffer中的字节数

	// 构造函数
	ByteBuffer();

	// 取出一个byte
	uint8_t getByte();

	// 写入一个byte
	void putByte(uint8_t b);

	// 设置byte数组
	void setData(uint8_t *buffer, int len);
};

• BitBuffer是一个bit的缓存，无论是将bit流转换为byte还是将byte转换为bit流，都将bit放在此结构体中进行缓存。
• ByteBuffer用来管理byte数组的缓存

这两个结构体中只向上层提供简单的get/put方法，不做任何的逻辑判断。也就是说只要调用了get方法就一定会有数据返回，调用了put方法就一定有空间存放数据。

BitStream

在编码时，需要将得到的bit流以byte的形式写出；解码则是将byte数组以bit流的形式读入。这就需要两种类型的bitstream：BitOutputStream和BitInputStream，其声明如下：

////////////////////////////////////////////////////////
//
// Bit Output Stream
//	将bit stream转化为byte数组
//  这里也只提供功能，至于byte缓存满的处理放到编码器中处理
//
////////////////////////////////////////////////////////
class BitOutputStream
{
	;
public:
	// 写入一个bit
	void putBit(bool b);

	// 写入多个相同的bit
	void putBit(bool b, int num);

	// 设置数据数组
	void setBuffer(uint8_t *buffer, int len);
	void resetBuffer();

	/*
		判断byte buffer中是可用的bit长度
	*/
	uint64_t freeLength();

	// Flush bit buffer to byte buffer
	bool flush();

	uint64_t getTotalCodeLength()
	{
		return bytes.pos;
	}

private:
	BitBuffer bits;
	ByteBuffer bytes;
};

class BitInputStream
{
public:
	// 读取一个bit
	bool getBit();

	// 设置byte buffer
	void setBuffer(uint8_t *buffer, int len);

	BufferState check();

private:
	BitBuffer bits;
	ByteBuffer bytes;
};

编码时需要BitOutputStream将bit流转换为byte数组，也就是个putBit的过程，需要注意的一点是在编码结束的时候需要调用方法flush，该函数有两个功能：

• 将BitBuffer中缓存的bit刷新到byte数组中
• 写入编码的编码终止符。编码终止符在解码过程中是一个很重要的判断标志，这里假定Golomb编码后码元的最大长度为64位，所以可设编码终止符为：连续64bits的0。在解码时，要判断接下来的是不是编码终止符。
• 将编码后输出的字节数填充为8（8 bytes，64 bits）的倍数，在解码时以8 bytes为单位进行解码，并且每次判断是不是编码终止符时也需要至少8 bytes。

编码/解码

有了BitStream的支持后，编解码过程是很简单的。

编码

每次编码前，首先计算编码后码元的长度，如果byte缓存空间不足以存放整个码元，则将byte buffer填充满后，剩余的部分，在bitset中缓存。返回false，指出缓存已满，需要处理缓存中的数据后才能继续编码或者更换一个新的Byte buffer存放编码后的数据.

bool GolombEncoder::encode(uint64_t num)
{
	uint64_t q = num >> k;
	uint64_t r = num & (m - 1);

	auto len = q + 1 + k; // 编码后码元的长度

	/*
	不会判断缓存是否为满，直接向里面放，不足的话缓存到bit buffer中
	*/
	bitStream.putBit(1, q);
	bitStream.putBit(0);

	for (int i = 0; i < k; i++)
	{
		bitStream.putBit(static_cast<bool>(r & 0x01));
		r >>= 1;
	}

	return bitStream.freeLength() >= len; // 空间足够，存放编码后的码元则返回true；否则返回false
}

上述代码以Golomb-Rice编码为例。在putBit时候的不会判断缓存是否够用，直接存放，如果Byte Buffer不足以存放本次编码的bits，则将Byte Buferr填充满后，余下的bits在BitBuffer中缓存，然后返回false，告诉调用者byte buffer已经填满，可以处理当前buffer的数据后调用resetBuffer后继续编码；也可以直接更换一个新的byte buffer。

解码

在每次解码前，先要调用check方法来判断byte buffer的状态，byte buffer中有以下几种状态

• 空，数据已读取完
• 编码终止符，buffer中的数据是编码终止符，解码结束
• 数据不足，buffer中的数据不足以完成本次解码，需要读取新的buffer
• 数据足够，继续解码

check的实现如下:

enum BufferState
{
	BUFFER_EMPTY, // buffer empty
	BUFFER_END_SYMBOL, // end_symbol 编码的中止符，已经没有编码的数据
	BUFFER_LACK, // buffer数据不足以完成解码，需要新的buffer
	BUFFER_ENGOUGH // 数据足够，继续解码
};

// 检测buffer的状态
// 在每次解码开始前调用
BufferState BitInputStream::check()
{
	// buffer中已无数据
	if (bits.count <= 0 && bytes.pos >= bytes.length)
		return BufferState::BUFFER_EMPTY;

	// buffer中还有数据，分为两种情况：不足64bits和有64bits
	auto count = (bytes.length - bytes.pos) * 8 + bits.count;

	// buffer中的数据足够64位
	if (count >= 64)
	{
		// bit buffer中数据就有64bits
		if (bits.count >= 64)
		{
			if (bits.data.none()) // 64 bits 0
				return BufferState::BUFFER_END_SYMBOL; // 编码中止符
			else
				return BufferState::BUFFER_ENGOUGH; // 数据足够继续解码
		}
		// bit buffer中的数据不足64bit
		else
		{

			if (!bits.data.none())
				return BufferState::BUFFER_ENGOUGH;

			int count = ((64 - bits.count) / 8 + 1);
			int index = 0;
			while (index < count)
			{
				auto b = bytes.data[bytes.pos + index];
				index++;
				if (b != 0)
					return BufferState::BUFFER_ENGOUGH;
			}

			return BUFFER_END_SYMBOL;
		}
	}
	// buffer中数据不足64位，不进行解码，
	// 将byte buffer中的数据取出放在bit buffer后，返回BUFFER_LACK
	else
	{
		while (bytes.pos < bytes.length)
		{
			auto b = bytes.getByte();
			bits.putByte(b);
		}
		return BufferState::BUFFER_LACK;
	}
}

check的过程有些复杂，但代码中的注释已足够清晰，这里就不再详述了。

Golomb-Rice的解码过程如下：

/////////////////////////////////////////////////////////
//
// 解码
// 在每次解码前需要check buffer的状态，根据不同的状态决定解码是否继续
//
///////////////////////////////////////////////////////
BufferState GolombDecoder::decode(uint64_t& num)
{
	auto state = bitStream.check();

	// buffer中数据足够，进行解码
	if (state == BufferState::BUFFER_ENGOUGH)
	{
        bool b;
        uint64_t unary = 0;
        b = bitStream.getBit();
        while (b)
        {
            unary++;
            b = bitStream.getBit();
        }

        std::bitset<64> bits;
        bits.reset();
        for (int i = 0; i < k; i++)
        {
            b = bitStream.getBit();
            bits.set(i, b);
        }

        num = unary * m + bits.to_ulong();
	}

	return state;
}

解码完成后会返回当前byte buffer的状态，

• 状态是BUFFER_END_SYMBOL，则解码过程已经完成
• 状态是BUFFER_EMPTY，byte buffer没有设置
• 状态是BUFFER_LACK，byte buffer中的数据不足以完成一次解码，需要读入新的数据
• 状态是BUFFER_ENGOUGH，byte buffer中的数据足够，继续下一次的解码

测试

仍然以Golomb-Rice编码为例，测试代码如下

	GolombEncoder encoder(m);
	encoder.setBuffer(buffer, 1024);

	ofstream ofs;
	ofs.open("golomb.gl", ios::binary);

	for (int i = 0; i < length; i++)
	{
		auto b = encoder.encode(nums[i]);
		if (!b)
		{
			cout << "Lack of buffer space,write the data to file" << endl;
			cout << "reset buffer" << endl;
			ofs.write((const char*)buffer, encoder.getToalCodeLength());

			encoder.resetBuffer();
			break;
		}
	}
	encoder.close();

	ofs.write((const char*)buffer, encoder.getToalCodeLength());

	ofs.close();

	cout << "Golomb finished coding" << endl;

• 实例编码器时，需要设定编码的参数m和以及存放编码后数据的buffer；
• 编码时，判断编码的的返回值，如果为true则继续编码，为false则buffer已满，将buffer写入文件后，resetBuffer继续编码。
• 编码结束后，调用close方法，写入编码终止符，并将整个编码后的数据填充为8的倍数。

下面代码Golomb-Rice的解码调用过程

	ifstream ifs;
	ifs.open("golomb.gl", ios::binary);

	memset(buffer, 0, 1024);

	ifs.read((char*)buffer, 664);

	ofstream encodeOfs;
	encodeOfs.open("encode.txt");

	GolombDecoder decoder(m);
	decoder.setBuffer(buffer, 1024);
	uint64_t num;
	auto state = decoder.decode(num);

	int index = 0;
	while (state != BufferState::BUFFER_END_SYMBOL)
	{
		encodeOfs << num << endl;
		state = decoder.decode(num);

		index++;
	}

	ifs.close();
	encodeOfs.close();

	cout << "decode finished" << endl;

编码是也需要根据返回的状态，来处理byte buffer，在上面已详述。

总结

终于完成了这篇博文，本文主要对Golomb编码进行了一个比较详尽的描述，包括Golomb编码的两个变种：Golomb-Rice和Exp-Golomb。在编码实现部分，难点有三个：

• byte数组和bit流之间的转换
• 需要一个唯一的编码终止符
• 解码时，byte buffer中剩余数据不足以完成一次解码

针对上述问题，做了如下工作：

• 实现了一个简单的BitStream库，能够方便在bit流和byte数组之间进行转换
• 对编码后的码元长度做了一个假设，其最长长度不会超过64位，这样就使用64比特的0作为编码的终止符
• 在编码的时，会将编码后的总字节数填充为8的倍数，解码的过程中就以8字节为单位进行，当byte buffer中的数据不足8字节时，可以判定当前buffer中的数据并不是全部的数据，需要继续读入数据已完成解码

本文所使用的源代码，

• Github https://github.com/brookicv/GolombCode
• CSDN http://download.csdn.net/detail/brookicv/9740838

2017年的第一篇博文，完。