react-native + teaset(Drawer)实现侧边菜单
1.代码
- /**
- * 购物车
- */
- import React, {Component} from 'react';
- import {
- View,
- Image,
- } from 'react-native';
- import { BaseContainer } from '../../../components';
- import Icon from 'react-native-vector-icons/Ionicons'; //引入图标
- import { Theme, Drawer, ListRow, Button } from 'teaset';
- import { images } from '../../../res';
- export default class ShopCarPage extends Component {
- constructor(props) {
- super(props);
- this.state = {
- rootTransform: 'none'
- };
- }
- // 显示或隐藏侧边菜单(抽屉)
- toggleMenu(side){
- let { rootTransform } = this.state;
- this.drawer = Drawer.open(this.renderDrawerMenu(), side, rootTransform);
- }
- // 侧边菜单(抽屉)
- renderDrawerMenu(){
- return (
- <View style={{backgroundColor: Theme.defaultColor, width: 260, flex: 1}}>
- <View style={{height: 60}} />
- <ListRow
- icon={
- <View style={{paddingRight: 12}}>
- <Image style={{width: 30, height: 30, tintColor: Theme.primaryColor}} source={images.error} />
- </View>
- }
- title='User name'
- />
- <ListRow
- icon={images.error}
- title='Home'
- />
- <ListRow
- icon={images.error}
- title='Store'
- bottomSeparator='none'
- />
- <View style={{flex: 1}} />
- <Button type='link' size='sm' title='Hide' onPress={() => this.drawer && this.drawer.close()} />
- </View>
- );
- }
- render() {
- return (
- <BaseContainer
- hideLeft
- title={'购物车'}
- rightView={<Icon name='md-home' size={30} onPress={() => this.toggleMenu('left')} />}
- >
- </BaseContainer>
- )
- }
- }
2.效果图
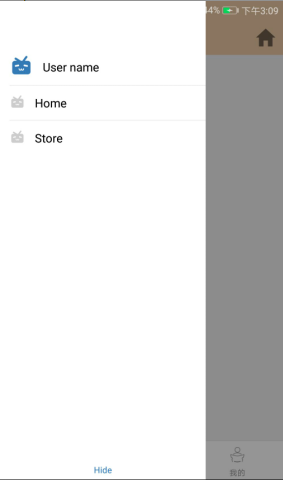
react-native + teaset(Drawer)实现侧边菜单的更多相关文章
- 虚拟机或真机调试React Native, 开启开发者菜单
虚拟机调试呼出开发者菜单,只需按下Ctrl+M组合键即可: 对于真机,通常摇晃手机可呼出,也可以在cmd输入adb shell input keyevent 82呼出菜单.如果还是不行,可能是系统管家 ...
- [RN] React Native 仿美团下拉筛选菜单控件
React Native 仿美团下拉筛选菜单控件 演示效果如下: 使用方法如下: 1.安装 npm install react-native-dropdownmenus --save react-na ...
- React Native填坑之旅--重新认识RN
如同黑夜里的一道光一样,就这么知道了F8. F8是每年一次Facebook每年一次的开发者大会.每次大会都会release相应的APP,iOS.Android都有.之前都是用Native开发的,但是2 ...
- React Native填坑之旅 -- 使用react-navigation代替Navigator
Navigator已经被React Native废弃了.也许你可以在另外的一个依赖库里react-native-deprecated-custom-components里找到.不过既然官方推荐的是re ...
- 【React Native开发】React Native控件之DrawerLayoutAndroid抽屉导航切换组件解说(13)
),请不要反复加群! 欢迎各位大牛,React Native技术爱好者增加交流!同一时候博客左側欢迎微信扫描关注订阅号,移动技术干货,精彩文章技术推送! 该DrawerLayoutAndroid组件封 ...
- React Native组件介绍
1.React Native目前已有的组件 ActivityIndicatorIOS:标准的旋转进度轮; DatePickerIOS:日期选择器: Image:图片控件: ListView:列表控件: ...
- windows 7下React Native环境配置
React Native 是 Facebook 推出的一个用 Java 语言就能同时编写 ios,android,以及后台的一项技术,它可以做到实时热更新 .FaceBook 也号称这们技术是 “Le ...
- React Native之坑总结(持续更新)
React Native之坑总结(持续更新) Genymotion安装与启动 之前我用的是蓝叠(BlueStack)模拟器,跑RN程序也遇到了一些问题,都通过搜索引擎解决了,不过没有记录. 但是Blu ...
- React Native APP结构探索
APP结构探索 我在Github上找到了一个有登陆界面,能从网上获取新闻信息的开源APP,想来研究一下APP的结构. 附上原网址:我的第一个React Native App 具体来讲,就是研究一个复杂 ...
随机推荐
- 第一篇:动态防火墙firewalld和静态防火墙iptables
动态防火墙firewalld firewalld提供了一个动态管理的防火墙,它支持网络(network)/防火墙区域(firewall zones )来定义网络连接( network connecti ...
- 如何在Android Studio中创建jniLib和asset文件夹 2
1.创建asset文件夹 如图进行操作 2.创建jniLib文件夹 —打开app下面的gradle文件(不是project的gradle) —在gradle文件的Android标签里面添加 sourc ...
- python 2 range, list, and set
这里主要说的是用python中的range来模拟for循环 转载请声明本文的引用出处:仰望大牛的小清新 1.range(var1,var2,var3): range产生一个列表(list),var1& ...
- 大数据DMP画像系统(转载 简介-龙果学院)
一.目标 1.掌握画像标签开发技巧 2.掌握数据挖掘技巧 3.了解业内画像和DMP系统的架构和开发 4.大数据结合业务场景落地 系统开发要求 涉及的技术要点:spark .elasticsearch. ...
- 洛谷——P1722 矩阵 II
P1722 矩阵 II 题目背景 usqwedf 改编系列题. 题目描述 如果你在百忙之中抽空看题,请自动跳到第六行. 众所周知,在中国古代算筹中,红为正,黑为负…… 给定一个1*(2n)的矩阵(us ...
- Jenkins获取分支的插件
Jenkins--->xxxx--->配置--->参数化构建过程--->选择Git Parameter Plug-In插件 Name: git_branch Descripti ...
- Python web 简单服务器的搭建与运行
搭建python的CGI环境: 假设在/var/www/cgi-bin下建立一个hello.py的文件 在ubuntu下打开终端 然后用命令 cd /var/www/ 进入后执行命令 : python ...
- 洛谷 P2742 [USACO5.1]圈奶牛Fencing the Cows
题目描述 农夫约翰想要建造一个围栏用来围住他的奶牛,可是他资金匮乏.他建造的围栏必须包括他的奶牛喜欢吃草的所有地点.对于给出的这些地点的坐标,计算最短的能够围住这些点的围栏的长度. 输入输出格式 输入 ...
- HDOJ 2582 f(n)
Discription This time I need you to calculate the f(n) . (3<=n<=1000000) f(n)= Gcd(3)+Gcd(4)+… ...
- 【基数排序】Divide by Zero 2017 and Codeforces Round #399 (Div. 1 + Div. 2, combined) C. Jon Snow and his Favourite Number
发现值域很小,而且怎么异或都不会超过1023……然后可以使用类似基数排序的思想,每次扫一遍就行了. 复杂度O(k*1024). #include<cstdio> #include<c ...
