[Contest20180314]学习

为了响应班级组团学习的要求，班主任xx将班上的$n$个同学编成了$m$个学习小组。

班长小r作为资深OI选手，他发现班级里存在一个可以量化的学习激♂情，并且这个激情跟组内成♀对的同学数量相关。若有$x$个人同在一个小组内一起学习，那么会增加$\left\lfloor\dfrac x2\right\rfloor$的学习激情。

因为xx所安排的一个同学可能属于多个学习小组，而每人一次又只能在一个小组中学习，小r意识到这里存在一个最大的学习激情。请你帮助小r，将同学们安排到特定的学习小组中一起学♂习，使学习激情最大。请注意你安排后的每个同学最多只能在$1$个小组中学习（他（她）也可以不在任何一个组学习，但这显然不够激♂情）。

shik：路径沿着花绕来绕去，绕得你晕头转向

之前听过“带花树”这个东西，以为是很恐怖的东西，现在学过觉得还行，不是那么难以理解

带花树算法可以找出一般图的最大匹配，效率居然和匈牙利算法是一样的$O(nm)$（如果忽略并查集）

演算法筆記已经讲得特别好了，以下主要是自己的一点理解

基础的思想是，我们从一个未匹配点开始，寻找一条路径使得匹配边和未匹配边交错出现，且最后一个点是未匹配点，将上面的路径取反后，匹配$+1$，不妨设这种路径为“交错路径”

因为我们用搜索的方式遍历图，所以对于找匹配，合法的搜索树上的每一条从根开始的路径都是交错路径

不妨设交错路径上到起点距离为偶数的点为“偶点”，反之为“奇点”，容易发现偶点的前一条边是匹配边，奇点的某条后一条边是匹配边

我们采用广搜，队列中只存偶点，假设当前队头是$x$，有边$(x,y)$

①如果$y$是奇点，不加入队列

②如果$y$未被匹配，那么很棒，我们已经找到增广路径了，把整条路径取反即可

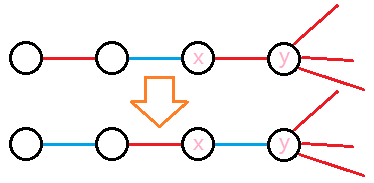
③如果$y$是偶点，那么会出现这种情况

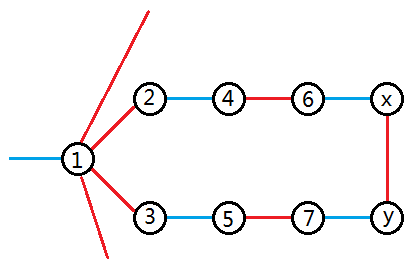
我们发现这种边$(x,y)$让搜索树上开了一朵花（一个奇环）

注意到$1$往$x$方向的奇点是$2$，$6$，$1$往$y$方向的奇点是$3$，$7$，可是我们发现的这条边$(x,y)$使得奇点全都消失了，因为先往$y$走，经过$(x,y)$再往原来的奇点走，走出来的路径长度是偶数（$1\rightarrow3\rightarrow5\rightarrow7\rightarrow y\rightarrow x\rightarrow6$），也就是说我们可以把这朵花上的所有点都看作偶点，不妨把它缩成一个偶点，并把原来的奇点加入到队尾（因为它们变成偶点了）

这里附上来自演算法筆記的一张图

缩花的过程可以用并查集实现，还需要找一下两个节点在搜索树中的最近公共祖先，暴力找就可以了

简单分析一下复杂度：最多广搜$n$次，每次广搜本身的复杂度是$O(n+m)$，因为每次缩花至少把$3$个点缩成$1$个点，所以每次广搜的缩花次数是$O(n)$的，总复杂度是$O\left(n(n+m)\alpha(n)\right)$

我写的代码参考自yay学长的博客，个人感觉他的代码风格挺好的

缩花的过程结合代码画一画图就很容易理解了

然后来做这道题

对于每组学生，分奇偶两种情况建图（黑色是原来的点，橙色是辅助点）

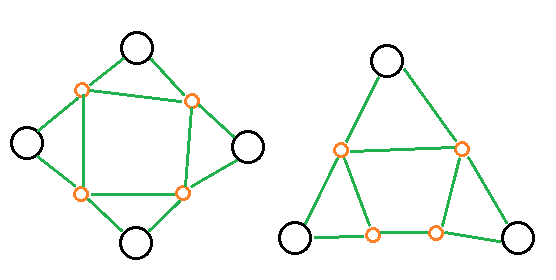
设加了$k$个辅助点，建出来的图跑最大匹配答案为$ans$，那么整道题的答案就是$ans-\dfrac k2$

做匹配的含义是：一条连接原来的点的匹配边$\Rightarrow$钦点这个同学属于哪组

在一组内，如果有$k$个辅助点，原来的点有$x$个未匹配，那么最大匹配为$\left\lfloor\dfrac{x+k}2\right\rfloor$

使用归纳法证明：

仅由$k$个点构成的环最大匹配为$\left\lfloor\dfrac k2\right\rfloor$

如果$k$是奇数，那么存在两条相邻的未匹配边，任选一条边，在外面加上一个原来的点，可以让匹配数$+1$，此时的最大匹配为$\left\lfloor\dfrac{k+1}2\right\rfloor$

之后，不管$k$是奇数还是偶数，每次按顺序在环上轮流加上两个原来的点，我们都可以找到一条增广路（因为环上的边是交错的，而新加入的点未匹配），让匹配数$+1$，也就是说，匹配数为$\left\lfloor\dfrac{x+k}2\right\rfloor$

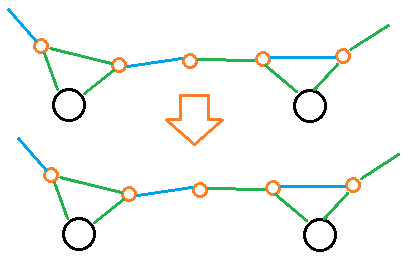
于是这题就做完了

e最后再说一个小技巧，做带花树之前贪心匹配一波可以让速度变快许多

#include<stdio.h>
#include<string.h>
#include<vector>
using namespace std;
int n,head,tail,h[9010],to[20010],nex[20010],q[20010],pre[9010],fa[9010],match[9010],type[9010],tm[9010],M;
void add(int a,int b){
	M++;
	to[M]=b;
	nex[M]=h[a];
	h[a]=M;
	M++;
	to[M]=a;
	nex[M]=h[b];
	h[b]=M;
}
int get(int x){return(fa[x]==x)?x:(fa[x]=get(fa[x]));}
int lca(int x,int y){
	M++;
	while(1){
		if(x){
			x=get(x);
			if(tm[x]==M)return x;
			tm[x]=M;
			x=pre[match[x]];
		}
		swap(x,y);
	}
}
void blossom(int x,int y,int p){
	while(get(x)!=p){
		pre[x]=y;
		y=match[x];
		if(type[y]==2){
			type[y]=1;
			tail++;
			q[tail]=y;
		}
		if(fa[x]==x)fa[x]=p;
		if(fa[y]==y)fa[y]=p;
		x=pre[y];
	}
}
int bfs(int x){
	M=0;
	int i,now,las;
	for(i=1;i<=n;i++)fa[i]=i;
	memset(pre,0,sizeof(pre));
	memset(type,0,sizeof(type));
	type[x]=1;
	head=tail=1;
	q[1]=x;
	while(head<=tail){
		x=q[head];
		head++;
		for(i=h[x];i;i=nex[i]){
			if(get(x)==get(to[i])||type[to[i]]==2)continue;
			if(type[to[i]]==0){
				type[to[i]]=2;
				pre[to[i]]=x;
				if(match[to[i]]==0){
					now=to[i];
					while(now){
						las=match[pre[now]];
						match[now]=pre[now];
						match[pre[now]]=now;
						now=las;
					}
					return 1;
				}
				type[match[to[i]]]=1;
				tail++;
				q[tail]=match[to[i]];
			}else{
				now=lca(x,to[i]);
				blossom(x,to[i],now);
				blossom(to[i],x,now);
			}
		}
	}
	return 0;
}
int greedy(){
	int x,i,s=0;
	for(x=1;x<=n;x++){
		if(match[x]==0){
			for(i=h[x];i;i=nex[i]){
				if(match[to[i]]==0){
					match[to[i]]=x;
					match[x]=to[i];
					s++;
					break;
				}
			}
		}
	}
	return s;
}
vector<int>stu[9010];
int c[9010];
int main(){
	int m,i,j,k,x;
	scanf("%d%d",&n,&m);
	while((n|m)!=0){
		memset(h,0,sizeof(h));
		c[0]=0;
		for(i=1;i<=m;i++){
			scanf("%d",c+i);
			if(c[i]>3)c[0]+=c[i];
			stu[i].clear();
			for(j=1;j<=c[i];j++){
				scanf("%d",&x);
				stu[i].push_back(x);
			}
		}
		M=0;
		for(i=1;i<=m;i++){
			if(c[i]<=3){
				for(j=0;j<c[i]-1;j++){
					for(k=j+1;k<c[i];k++)add(stu[i][j],stu[i][k]);
				}
			}else{
				for(j=0;j<c[i]-1;j++){
					add(stu[i][j],n+j+1);
					add(n+j+1,stu[i][j+1]);
				}
				add(stu[i][c[i]-1],n+c[i]);
				if(c[i]&1){
					add(n+c[i]+1,stu[i][0]);
					add(n+c[i]+1,n+1);
					for(j=n+1;j<=n+c[i];j++)add(j,j+1);
					n+=c[i]+1;
					c[0]++;
				}else{
					add(n+c[i],stu[i][0]);
					add(n+c[i],n+1);
					for(j=n+1;j<n+c[i];j++)add(j,j+1);
					n+=c[i];
				}
			}
		}
		memset(match,0,sizeof(match));
		memset(tm,0,sizeof(tm));
		x=greedy();
		for(i=1;i<=n;i++){
			if(match[i]==0)x+=bfs(i);
		}
		printf("%d\n",x-c[0]/2);
		scanf("%d%d",&n,&m);
	}
}