DP的四边形优化

DP的四边形优化

一、进行四边形优化需要满足的条件

　　1、状态转移方程如下：

　　　　

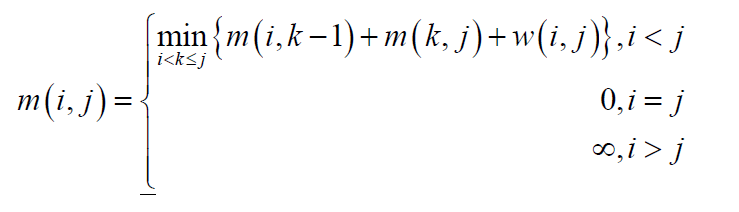
　　　　　　m(i,j)表示对应i,j情况下的最优值。

　　　　　　w(i,j)表示从i到j的代价。

　　　　　　例如在合并石子中：

　　　　　　　　m(i,j)表示从第i堆石子合并到j堆石子合并成一堆的最小代价。

　　　　　　　　w(i,j)表示从第i堆石子到第j堆石子的重量和。

　　2、函数w满足区间包含的单调性和四边形不等式

　　　　　　　

二、满足上述条件之后的两条定理

　　1、假如函数w满足上述条件，那么函数m 也满足四边形不等式，即

　　　　

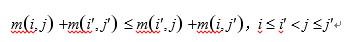
　　　　例如:

　　　　　　　　假如有：w(1, 3) + w(2, 4) £ w(2, 3) + w(1, 4)，

　　　　　　　　m(1, 3) + m(2, 4) £ m(2, 3) + m(1, 4)，

　　2、假如m(i, j)满足四边形不等式，那么s (i, j)单调，即：

　　　　

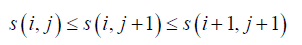
三、如何使用

　　运用上面两条定理，可以将最上面的DP状态转移方程变为如下：

　　　　

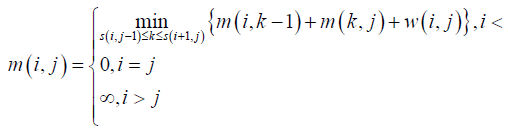
四、具体应用

　　用四边形优化将合并石子(直线型)的时间复杂度化为 O(n*n)

　　

 #include <iostream>
 #include <string.h>
 #include <stdio.h>

 using namespace std;
 const int INF =  << ;
 const int N = ;

 int dp[N][N];
 int p[N][N];
 int sum[N];
 int n;

 int getMinval()
 {
     for(int i=; i<=n; i++)
     {
         dp[i][i] = ;
         p[i][i] = i;
     }
     for(int len=; len<n; len++)
     {
         for(int i=; i+len<=n; i++)
         {
             int end = i+len;
             int tmp = INF;
             int k = ;
             for(int j=p[i][end-1]; j<=p[i+1][end]; j++)
             {
                 if(dp[i][j] + dp[j+][end] + sum[end] - sum[i-] < tmp)
                 {
                     tmp = dp[i][j] + dp[j+][end] + sum[end] - sum[i-];
                     k = j;
                 }
             }
             dp[i][end] = tmp;
             p[i][end] = k;
         }
     }
     return dp[][n];
 }

 int main()
 {
     while(scanf("%d",&n)!=EOF)
     {
         sum[] = ;
         for(int i=; i<=n; i++)
         {
             int val;
             scanf("%d",&val);
             sum[i] = sum[i-] + val;
         }
         printf("%d\n",getMinval());
     }
     return ;
 }

上述代码具体在内存中的运行过程：