决策树--Python

决策树

实验集数据：

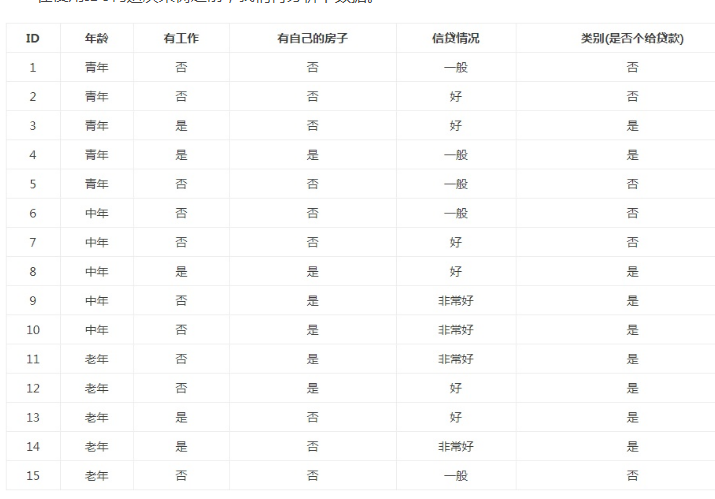
#coding:utf8

#关键词：决策树(desision tree)、特征选择、信息增益(information gain)、香农熵、熵(entropy)、经验熵(H(D))、节点(node)、有向边(directed edge)、根节点(root node)、叶节点(leaf node)、判断模块(decision block)、终止模块(terminating block)、分支(branch)、最优特征、

import requests
import requests, json, time, re, os, sys, time
import codecs
import shutil
from sgmllib import SGMLParser
from pyquery import PyQuery as pq
from lxml import etree
import urllib2
import json
import random
#from math import log
import math
sys.path.append('/home/shutong/crawl/script/media')
from tools import *

from numpy import *
import operator

reload(sys)
sys.setdefaultencoding("utf-8")

#年龄：0代表青年，1代表中年，2代表老年；
#有工作：0代表否，1代表是；
#有自己的房子：0代表否，1代表是；
#信贷情况：0代表一般，1代表好，2代表非常好；
#类别(是否给贷款)：no代表否，yes代表是

def createDataSet():
    dataSet = [[0,0,0,0,'no'],[0,0,0,1,'no'],[0,1,0,1,'yes'],[0,1,1,0,'yes'],[0,0,0,0,'no'],[1,0,0,0,'no'],[1,0,0,1,'no'],[1,1,1,1,'yes'],[1,0,1,2,'yes'],[1,0,1,2,'yes'],[2,0,1,2,'yes'],[2,0,1,1,'yes'],[2,1,0,1,'yes'],[2,1,0,2,'yes'],[2,0,0,0,'no']]
    #labels = ['不放贷','放贷']
    labels = ['年龄', '有工作', '有自己的房子', '信贷情况']
    return dataSet,labels

#计算经验熵
#输入:dataSet
#输出:经验熵(香农熵)
def calcShannonEnt(dataSet):
    #print dataSet
    #返回数据集的行数
    numEntires = len(dataSet)
    #保存每个标签(Label)出现次数的字典
    labelCounts = {}
    #对每组特征向量进行统计
    for featVec in dataSet:
        #提取标签(Label)信息
        currentLabel = featVec[-1]
        #如果标签(Label)没有放入统计次数的字典,添加进去
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        #Label计数
        labelCounts[currentLabel] += 1
    #经验熵(香农熵)
    shannonEnt = 0.0
    #计算香农熵
    for key in labelCounts:
        #选择该标签(Label)的概率
        prob = float(labelCounts[key]) / numEntires
        #print prob,math.log(prob,2)
        shannonEnt -= prob * math.log(prob, 2)
    #返回经验熵(香农熵)
    return shannonEnt

#函数说明:按照给定特征划分数据集
#splitDataSet函数是用来选择各个特征的子集的
def splitDataSet(dataSet, axis, value):
    #创建返回的数据集列表
    retDataSet = []
    #遍历数据集
    for featVec in dataSet:
        if featVec[axis] == value:
            #去掉axis特征
            reducedFeatVec = featVec[:axis]
            #将符合条件的添加到返回的数据集
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet  

#计算信息增益
def chooseBestFeatureToSplit(dataSet):
    #特征数量,去除最后一列，其余字段最为特征变量
    numFeatures = len(dataSet[0]) - 1
    #计算数据集的香农熵
    baseEntropy = calcShannonEnt(dataSet)
    #信息增益
    bestInfoGain = 0.0
    #最优特征的索引值,最初默认取-1
    bestFeature = -1
    #遍历所有特征
    for i in range(numFeatures):
        #获取dataSet的第i个所有特征
        featList = [example[i] for example in dataSet]
        #创建set集合{},元素不可重复
        uniqueVals = set(featList)
        #经验条件熵
        newEntropy = 0.0
        #计算信息增益
        for value in uniqueVals:
            #subDataSet划分后的子集
            subDataSet = splitDataSet(dataSet, i, value)
            #计算子集的概率
            prob = len(subDataSet) / float(len(dataSet))
            #根据公式计算经验条件熵
            newEntropy += prob * calcShannonEnt(subDataSet)
        #信息增益
        infoGain = baseEntropy - newEntropy
        #打印每个特征的信息增益
        print("第%d个特征的增益为%.3f" % (i, infoGain))
        #计算信息增益
        #更新信息增益，找到最大的信息增益
        if (infoGain > bestInfoGain):
            bestInfoGain = infoGain
            #记录信息增益最大的特征的索引值
            bestFeature = i
    return bestFeature

#统计classList中出现此处最多的元素(类标签)
def majorityCnt(classList):
    classCount = {}
    for vote in classList:                                        #统计classList中每个元素出现的次数
        if vote not in classCount.keys():classCount[vote] = 0
        classCount[vote] += 1
    #根据字典的值降序排序
    sortedClassCount = sorted(classCount.items(), key = operator.itemgetter(1), reverse = True)
    #返回classList中出现次数最多的元素
    return sortedClassCount[0][0]

#创建决策树[递归]
def createTree(dataSet, labels, featLabels):
    #取分类标签(是否放贷:yes or no)
    classList = [example[-1] for example in dataSet]
    #如果类别完全相同则停止继续划分[第一个标签数等于所有的标签数,说明所有的结果都是同一个标签]
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    #len(dataSet[0])为特征变量数
    if len(dataSet[0]) == 1:                                    #遍历完所有特征时返回出现次数最多的类标签
        return majorityCnt(classList)
    #选择最优特征
    bestFeat = chooseBestFeatureToSplit(dataSet)
    ##最优特征的标签
    bestFeatLabel = labels[bestFeat]
    featLabels.append(bestFeatLabel)
    #print bestFeat,bestFeatLabel,featLabels
    ##根据最优特征的标签生成树
    myTree = {bestFeatLabel:{}}
    print myTree
    ##删除已经使用特征标签
    del(labels[bestFeat])
    ##得到训练集中所有最优特征的属性值
    featValues = [example[bestFeat] for example in dataSet]
    ##去掉重复的属性值
    uniqueVals = set(featValues)
    #print uniqueVals
    for value in uniqueVals:                                    #遍历特征，创建决策树。
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), labels, featLabels)
    return myTree
#dataSet,labels = createDataSet()
#print calcShannonEnt(dataSet)
#print("最优特征索引值:" + str(chooseBestFeatureToSplit(dataSet)))

#获取决策树叶子结点的数目
def getNumLeafs(myTree):
    #初始化叶子
    numLeafs = 0
    firstStr = next(iter(myTree))#python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性，可以使用list(myTree.keys())[0]
    #获取下一组字典
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':                #测试该结点是否为字典，如果不是字典，代表此结点为叶子结点
            numLeafs += getNumLeafs(secondDict[key])
        else:   numLeafs +=1
    return numLeafs

def getTreeDepth(myTree):
    #初始化决策树深度
    maxDepth = 0
    firstStr = next(iter(myTree))                                #python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性，可以使用list(myTree.keys())[0]
    #获取下一个字典
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':                #测试该结点是否为字典，如果不是字典，代表此结点为叶子结点
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:   thisDepth = 1
        #更新层数
        if thisDepth > maxDepth: maxDepth = thisDepth
    return maxDepth

#使用决策树分类
#inputTree - 已经生成的决策树
#featLabels - 存储选择的最优特征标签
#testVec - 测试数据列表，顺序对应最优特征标签
def classify(inputTree, featLabels, testVec):
    firstStr = next(iter(inputTree))                                                        #获取决策树结点
    secondDict = inputTree[firstStr]                                                        #下一个字典
    featIndex = featLabels.index(firstStr)
    for key in secondDict.keys():
        if testVec[featIndex] == key:
            if type(secondDict[key]).__name__ == 'dict':
                classLabel = classify(secondDict[key], featLabels, testVec)
            else: classLabel = secondDict[key]
    return classLabel

#测试数据集
dataSet, labels = createDataSet()
featLabels = []
#创建决策树
myTree = createTree(dataSet, labels, featLabels)

#测试数据
testVec = [0,0]
#测试结果
result = classify(myTree, featLabels, testVec)
if result == 'yes':
    print('放贷')
if result == 'no':
    print('不放贷')

#print myTree
#print getNumLeafs(myTree)
#print getTreeDepth(myTree)