D. Relatively Prime Graph

Let's call an undirected graph G=(V,E)G=(V,E) relatively prime if and only if for each edge (v,u)∈E(v,u)∈E  GCD(v,u)=1GCD(v,u)=1 (the greatest common divisor of vv and uu is 11). If there is no edge between some pair of vertices vv and uu then the value of GCD(v,u)GCD(v,u) doesn't matter. The vertices are numbered from 11 to |V||V|.

Construct a relatively prime graph with nn vertices and mm edges such that it is connected and it contains neither self-loops nor multiple edges.

If there exists no valid graph with the given number of vertices and edges then output "Impossible".

If there are multiple answers then print any of them.

Input

The only line contains two integers nn and mm (1≤n,m≤1051≤n,m≤105) — the number of vertices and the number of edges.

Output

If there exists no valid graph with the given number of vertices and edges then output "Impossible".

Otherwise print the answer in the following format:

The first line should contain the word "Possible".

The ii-th of the next mm lines should contain the ii-th edge (vi,ui)(vi,ui) of the resulting graph (1≤vi,ui≤n,vi≠ui1≤vi,ui≤n,vi≠ui). For each pair (v,u)(v,u)there can be no more pairs (v,u)(v,u) or (u,v)(u,v). The vertices are numbered from 11 to nn.

If there are multiple answers then print any of them.

Examples

input

Copy

5 6

output

Copy

Possible
2 5
3 2
5 1
3 4
4 1
5 4

input

Copy

6 12

output

Copy

Impossible

Note

Here is the representation of the graph from the first example: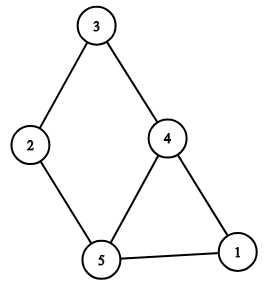

这题无脑暴力 暴力真的出了奇迹

暴力枚举一遍就行了

 #include <bits/stdc++.h>
 using namespace std;
 const int maxn = 1e5 + ;
 const int INF = 0x3fffffff;
 typedef long long LL;
 using namespace std;
 int n, m;
 struct node {
     int x, y;
     node () {}
     node (int x, int y): x(x), y(y) {}
 } qu[maxn];
 int main() {
     scanf("%d%d", &n, &m);
     if (n -  > m) {
         printf("Impossible\n");
         return ;
     }
     int k = , flag = ;
     for (int i =  ; i <= n ; i++) {
         for (int j = i +  ; j <= n ; j++) {
             if (__gcd(i, j) == ) qu[k++] = node(i, j);
             if (k == m) {
                 flag = ;
                 break;
             }
         }
         if (flag) break;
     }
     if (flag) {
         printf("Possible\n");
         for (int i =  ; i < k ; i++)
             printf("%d %d\n", qu[i].x, qu[i].y);
     } else  printf("Impossible\n");
     return ;
 }