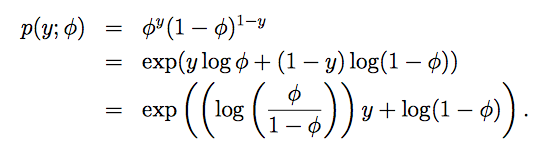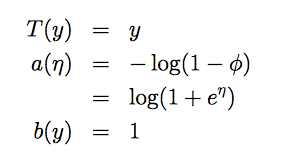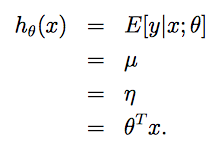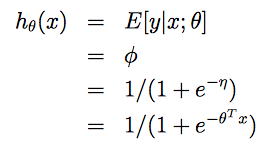斯坦福CS229机器学习课程笔记 part3:广义线性模型 Greneralized Linear Models (GLMs)
指数分布族 The exponential family
因为广义线性模型是围绕指数分布族的。大多数常用分布都属于指数分布族,服从指数分布族的条件是概率分布可以写成如下形式:
η 被称作自然参数(natural parameter),或正则参数canonical parameter),它是指数分布族唯一的参数
T(y) 被称作充分统计量(sufficient statistic),很多情况下T(y)=y log
a(η) 是log partition function
e-a(η)是一个规范化常数,使得分布p(y; η)的和为1p(;η)
对于给定的一组a,b,T,都会得到对应的指数分布族。改变参数η的取值会影响该指数族的分布。
伯努利分布(Bernoulli)的指数分布族
对应关系如下:
η 为标量,转置等于其本身。所以:

高斯分布(Gaussian)的指数分布族
正态分布(正态分布有两个参数均值 μ 与 标准差σ,在做线性回归的时候,我们关心的是均值而标准差不影模型的学习与参数θ的选择,因此这里将 σ2设为1便于计算)
对应关系如下:
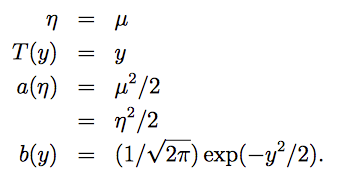
以下分布也都属于指数分布族
Bernoulli 伯努利分布
Gaussian 高斯分布
multinomial 多项式分布
Poisson 泊松分布(用于计数的建模)
gamma 伽马分布、exponential 指数分布(用于对正数建模,多用于间隔问题)
β 分布,Dirichlet 分布(用于对小数建模)
广义线性模型 Greneralized Linear Models
广义线性模型(Generalized Linear Models)
使用GLMs来解决问题,基于三个设计假设:
- y|x;θ∼ExponentialFamily(η)。输出变量基于输入变量的条件概率分布服从指数分布族
- 我们的目标是通过给定x,来预测T(y)期望 E[T(y) | x]。对于给定的输入变量x,学习的目标是预测T(y)的期望值,T(y)经常就是y,因此假设函数需要满足h(x)=E[y|x](这个假设对logistic回归和线性回归都成立)。
- 自然函数 η 与输入特征 x 的关系是线性的,η=θTx(如果自然参数是向量,ηi=θTix)。
如果问题满足这三个假设,就可以构造广义线性模型来解决。这三个假设指明了如何从输入变量映射到输出变量与概率模型。
最小二乘法
在线性回归的最小平方问题中,目标变量 y 是连续的(在GLM的术语中也称作响应变量(response variable))。
已知给定x,y符合高斯分布,均值为 μ。线性回归目标是预测T(y)的期望(期望也就是均值 μ)。又根据上面对于高斯分布指数分布族的推导,得知T(y)=y,μ=η。由GLMs 假设3得知 η=θTx。
最终得到线性回归的假设函数:
Logistic回归
在二元分类问题中,给定x,y服从伯努利分布,均值为ϕ。由伯努利分布的 η ,可以反推出 φ

利用广义线性模型的假设 3 可知同时有 η=θTx。因此可以得到logistic回归的假设函数(sigmoid 函数):
canonical response function:g(η) = E[T(y); η],给定正则参数 η,求分布的平均值
canonical link function:g−1,canonical response function的逆,即根据g(η)求 η
Softmax回归
Logistic 分布解决二分类问题,Softmax用于解决多分类问题。

符合多项式分布multinomial distribution。下面开始构建模型,使其符合指数分布。
如果有k个类型 y∈{1,2,...,k}。则可以用 φ1,φ2,...,φk−1,φk 一共k个变量来表示 y属于每种类型的概率。但因为所有概率之和为1,如果已知前 k-1个概率的值,第k个概率就确定了,这将违反独立同分布的原则。
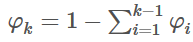
因此我们用前面 k-1 个变量替代第 k 个变量,设置参数:φ1,φ2,...,φk−1。其中 φi = p(y=i; φ)。
【注:虽然有时公式中会将φk写出来,但要记住它是一个由k-1项决定的表达式,不是一个变量】
引入T(y):

注意,这里就和前面的 T(y) = y 不同,这里的 T(y)是一个向量,所以用 T(y)i 表示 T(y) 的第i个元素。
引出 indicator function 指示函数 的定义:1{True}=1,1{False}=0。
由于当 i = 1 时T(1)为1。当 i = 2 时T(2)为1。即当且仅当 y = i 时,T(y)i =1。则T(y)与y的关系可以写成:

有 T(y)i 的期望等于 “y属于类型 i 的概率φi ”:
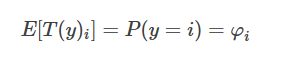
现在可以证明多项式分布符合指数分布族:
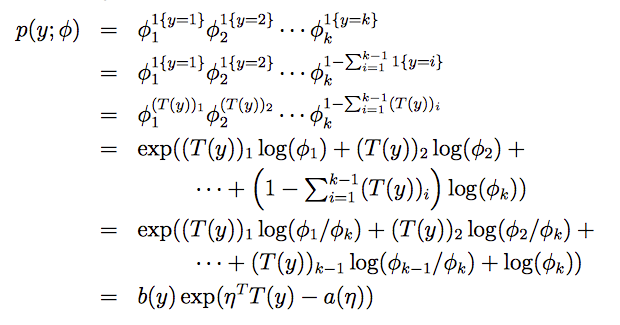
公式 第4步到第5步,是将最后一个乘积的和分配到前面每一项上做减法。且 log(a)-log(b) = log(a/b)。
对应关系:
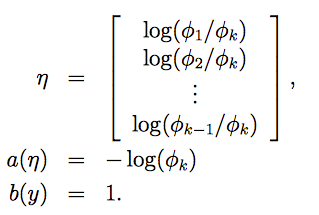
link函数为:

为了方便,定义 ηk = log(φk/φk) = 0。通过上式反推 φ:

公式两边 k 项求和:
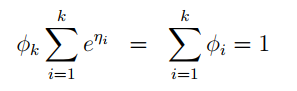
移项:
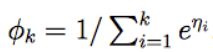
再带回 (7)式中替换φk。移项得到从η到φ’s的映射,称作softmax函数:
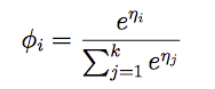
根据假设3,并令

得到softmax regression,它是logistic regression的推广。根据机器学习三要素,其
(1)模型

其中 eμk = e0 = 1。
最终,假设函数为:

(2)策略
依然可以使用极大似然估计的方法来学习θ,似然函数 L(θ) 为m个概率 p(y(i)|x(i); θ) 的乘积。其对数 l(θ)为: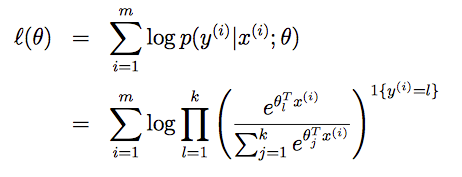
(3)算法
可以通过梯度上升或牛顿方法来求出合适的参数 θ。这里μ是上面的指示函数1{}
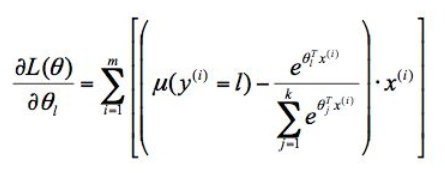
梯度上升:

Softmax 回归和 Logistic回归的关系



斯坦福CS229机器学习课程笔记 part3:广义线性模型 Greneralized Linear Models (GLMs)的更多相关文章
- 斯坦福CS229机器学习课程笔记 Part1:线性回归 Linear Regression
机器学习三要素 机器学习的三要素为:模型.策略.算法. 模型:就是所要学习的条件概率分布或决策函数.线性回归模型 策略:按照什么样的准则学习或选择最优的模型.最小化均方误差,即所谓的 least-sq ...
- 斯坦福CS229机器学习课程笔记 part2:分类和逻辑回归 Classificatiion and logistic regression
Logistic Regression 逻辑回归 1.模型 逻辑回归解决的是分类问题,并且是二元分类问题(binary classification),y只有0,1两个取值.对于分类问题使用线性回归不 ...
- 广义线性模型(Generalized Linear Models)
在线性回归问题中,我们假设,而在分类问题中,我们假设,它们都是广义线性模型的例子,而广义线性模型就是把自变量的线性预测函数当作因变量的估计值.很多模型都是基于广义线性模型的,例如,传统的线性回归模型, ...
- Andrew 机器学习课程笔记
Andrew 机器学习课程笔记 完成 Andrew 的课程结束至今已有一段时间,课程介绍深入浅出,很好的解释了模型的基本原理以及应用.在我看来这是个很好的入门视频,他老人家现在又出了一门 deep l ...
- 【读书笔记与思考】Andrew 机器学习课程笔记
Andrew 机器学习课程笔记 完成 Andrew 的课程结束至今已有一段时间,课程介绍深入浅出,很好的解释了模型的基本原理以及应用.在我看来这是个很好的入门视频,他老人家现在又出了一门 deep l ...
- CS229 机器学习课程复习材料-线性代数
本文是斯坦福大学CS 229机器学习课程的基础材料,原始文件下载 原文作者:Zico Kolter,修改:Chuong Do, Tengyu Ma 翻译:黄海广 备注:请关注github的更新,线性代 ...
- CS229 机器学习课程复习材料-概率论
本文是斯坦福大学CS229机器学习课程的基础材料,原始文件下载 原文作者:Arian Maleki , Tom Do 翻译:石振宇 审核和修改制作:黄海广 备注:请关注github的更新. CS229 ...
- Andrew Ng机器学习课程笔记(三)之正则化
Andrew Ng机器学习课程笔记(三)之正则化 版权声明:本文为博主原创文章,转载请指明转载地址 http://www.cnblogs.com/fydeblog/p/7365475.html 前言 ...
- Andrew Ng机器学习课程笔记(五)之应用机器学习的建议
Andrew Ng机器学习课程笔记(五)之 应用机器学习的建议 版权声明:本文为博主原创文章,转载请指明转载地址 http://www.cnblogs.com/fydeblog/p/7368472.h ...
随机推荐
- mcake活动维护,检查 ★ ★
一.检查火狐浏览器.chrome浏览器.ie8.9.10.11是否显示正常 二.对比设计稿 三.动画添加 四.检查图片是否失真 五.ie8空按钮无法点击 六.官网banner制作
- JavaScript能做的事 是不是jQuery都能做>?
比如修改表单中的action 并实现跳转 问题是此时没有点击表单中的submit 提交按钮?
- L140
一本载有许多时装照片的杂志是用带有光泽的优质纸印制的.A glossy magazine has lots of pictures of fashionable clothes and is prin ...
- SpringMVC札集(01)——SpringMVC入门完整详细示例(上)
自定义View系列教程00–推翻自己和过往,重学自定义View 自定义View系列教程01–常用工具介绍 自定义View系列教程02–onMeasure源码详尽分析 自定义View系列教程03–onL ...
- tf随笔-6
import tensorflow as tfx=tf.constant([-0.2,0.5,43.98,-23.1,26.58])y=tf.clip_by_value(x,1e-10,1.0)ses ...
- Quartz 2D编程指南(1) - 概览
Quartz 2D编程指南是论坛会员德鲁伊翻译的国外的Quartz 2D一系列学习资料,供大家参考 Quartz 2D是一个二维图形绘制引擎,支持iOS环境和Mac OS X环境.我们可以使用Quar ...
- 51nod 1298 圆与三角形
给出圆的圆心和半径,以及三角形的三个顶点,问圆同三角形是否相交.相交输出"Yes",否则输出"No".(三角形的面积大于0). 输入 第1行:一个数 ...
- CentOS 7 : Docker私有仓库搭建和使用
系统环境: CentOS 7.2 192.168.0.179:docker仓库 192.168.0.60:客户端 安装并启动docker yum -y install docker systemctl ...
- RelativeLayout里的gravity不能居中的解决方法
最近在遇到RelativeLayout里的gravity属性给它复制center_horizontal或者center都不能居中它的子组件,后来找到了替代方法,只要在它的每个子组件里加上android ...
- python中的configparse学习笔记
configparse主要用于在python中进行配置文件的读取. 基本的读取配置文件: -read(filename) 直接读取ini文件内容 -sections() 得到所有的section,并以 ...