NOI2012 魔幻棋盘

http://www.lydsy.com/JudgeOnline/problem.php?id=2877

二维线段树。

好恶。。。。。。

B类数据：

棋盘是一维的。

我们有一个结论：

$gcd(a_{1},a_{2},...,a_{n-1},a_{n})=gcd(a_{2}-a_{1},a_{3}-a_{2},...,a_{n}-a_{n-1},a_{1})$

证明：

假设集合A是a1,a2,...,an-1,an的所有公约数的集合，集合B是a2-a1,a3-a2,...,an-an-1,a1的所有公约数的集合。

对于所有的r∈A，r|a1,r|a2,...,r|an-1,r|an。

其必满足r|a2-a1,r|a3-a2,...,r|an-an-1,r|a1。

所以A⊆B。

对于所有的r∈B，r|a1,r|a2-a1,r|a3-a2,...,r|an-an-1。

其必满足：

∵r|a1，r|a2-a1

∴r|{a1-(a2-a1)}  ==>  r|-a2   ==> r|a2

∵r|a2，r|a3-a2

∴r|{a2-(a3-a2)}  ==>  r|-a3   ==> r|a3

......

∵r|an-1，r|an-an-1

∴r|{an-1 - (an - an-1)}  ==>  r|-an   ==> r|an

所以B⊆A。

故A=B。

所以：

$gcd(a_{1},a_{2},...,a_{n-1},a_{n})=gcd(a_{2}-a_{1},a_{3}-a_{2},...,a_{n}-a_{n-1},a_{1})$

我们记b[i]=a[i]-a[i-1]。

假设询问[l,R]中的最大公约数，其实就是求gcd(a[L],gcd(b[L+1]...b[R]))。

如果将[l,R]中数都加上C，其实就是a[L...R]加上C,b[L]加上C，b[R+1]减去C。

这可以用2棵线段树维护。

C类数据：

棋盘是二维的。

我们可以从一维推广一下。

原本是这样的：

$a_{4,1},a_{4,2},a_{4,3},a_{4,4}$
$a_{3,1},a_{3,2},a_{3,3},a_{3,4}$
$a_{2,1},a_{2,2},a_{2,3},a_{2,4}$
$a_{1,1},a_{1,2},a_{1,3},a_{1,4}$

右减左：

$a_{4,1},a_{4,2}-a_{4,1},a_{4,3}-a_{4,2},a_{4,4}-a_{4,3}$

$a_{3,1},a_{3,2}-a_{3,1},a_{3,3}-a_{3,2},a_{3,4}-a_{3,3}$

$a_{2,1},a_{2,2}-a_{2,1},a_{2,3}-a_{2,2},a_{2,4}-a_{2,3}$

$a_{1,1},a_{1,2}-a_{1,1},a_{1,3}-a_{1,2},a_{1,4}-a_{1,3}$

上减下：

$a_{4,1}-a_{3,1},a_{4,2}-a_{4,1}-a_{3,2}+a_{3,1},a_{4,3}-a_{4,2}-a_{3,3}+a_{3,2},a_{4,4}-a_{4,3}-a_{3,4}+a_{3,3}$

$a_{3,1}-a_{2,1},a_{3,2}-a_{3,1}-a_{2,2}+a_{2,1},a_{3,3}-a_{3,2}-a_{2,3}+a_{2,2},a_{3,4}-a_{3,3}-a_{2,4}+a_{2,3}$

$a_{2,1}-a_{1,1},a_{2,2}-a_{2,1}-a_{1,2}+a_{1,1},a_{2,3}-a_{2,2}-a_{1,3}+a_{1,2},a_{2,4}-a_{2,3}-a_{1,4}+a_{1,3}$

$a_{1,1} , a_{1,2}-a_{1,1}, a_{1,3}-a_{1,2}, a_{1,4}-a_{1,3}$

其实就是变成了b[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]

我们在原图中以(X,Y)为原点建立平面直角坐标系，将棋盘分成四部分，每个部分的操作时一样的。

1：

以(x1,y1)为左下角，(x2,y2)为右上角的矩形区域都加C。

我们发现只有(x1,y1),(x1,y2+1),(x2+1,y1),(x2+1,y2+1)发生了改变。

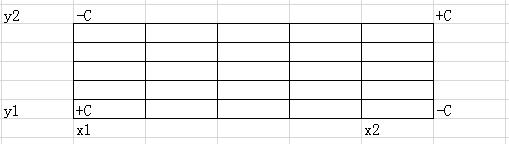
单点修改，可以用二维线段树。

注意在第一维线段树中，对于非叶子节点，我们更新的时候要要从子节点中得到更新。

2：

求以(1,1)为左下角，(x,y)为右上角的矩形区间的gcd。

直接在二维线段树中询问。

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<fstream>
#include<algorithm>
#include<cstring>
#include<string>
#include<cmath>
#include<queue>
#include<stack>
#include<map>
#include<utility>
#include<set>
#include<bitset>
#include<vector>
#include<functional>
#include<deque>
#include<cctype>
#include<climits>
#include<complex>
//#include<bits/stdc++.h>适用于CF,UOJ，但不适用于poj

using namespace std;

typedef long long LL;
typedef double DB;
typedef pair<int,int> PII;
typedef complex<DB> CP;

#define mmst(a,v) memset(a,v,sizeof(a))
#define mmcy(a,b) memcpy(a,b,sizeof(a))
#define re(i,a,b)  for(i=a;i<=b;i++)
#define red(i,a,b) for(i=a;i>=b;i--)
#define fi first
#define se second
#define m_p(a,b) make_pair(a,b)
#define SF scanf
#define PF printf
#define two(k) (1<<(k))

template<class T>inline T sqr(T x){return x*x;}
template<class T>inline void upmin(T &t,T tmp){if(t>tmp)t=tmp;}
template<class T>inline void upmax(T &t,T tmp){if(t<tmp)t=tmp;}

const DB EPS=1e-;
inline int sgn(DB x){if(abs(x)<EPS)return ;return(x>)?:-;}
const DB Pi=acos(-1.0);

inline int gint()
  {
        int res=;bool neg=;char z;
        for(z=getchar();z!=EOF && z!='-' && !isdigit(z);z=getchar());
        if(z==EOF)return ;
        if(z=='-'){neg=;z=getchar();}
        for(;z!=EOF && isdigit(z);res=res*+z-'',z=getchar());
        return (neg)?-res:res;
    }
inline LL gll()
  {
      LL res=;bool neg=;char z;
        for(z=getchar();z!=EOF && z!='-' && !isdigit(z);z=getchar());
        if(z==EOF)return ;
        if(z=='-'){neg=;z=getchar();}
        for(;z!=EOF && isdigit(z);res=res*+z-'',z=getchar());
        return (neg)?-res:res;
    }

const int maxN=;

int N,M,X,Y,T;
vector<LL> mp[maxN+];

inline LL gcd(LL a,LL b){LL ta,tb;if(a<) a=-a;if(b<) b=-b;for(;b!=;ta=b,tb=a%b,a=ta,b=tb);return a;}

struct Tnode
  {
      Tnode *l,*r;LL v;
      inline Tnode(){l=r=;v=;}
      inline LL lv(){return l?l->v:;}
      inline LL rv(){return r?r->v:;}
  };
Tnode mem[];
int MID=-;
inline Tnode *New_Node(){mem[++MID]=Tnode();return mem+MID;}

struct Tdata
{

  int N,M;
    Tnode *root[*maxN+];
    inline void clear(int _N,int _M){N=_N;M=_M;}

  inline void update1(Tnode *&rt,int l,int r,int x,LL C)
    {
          if(l>r || x<l || r<x) return;
          if(!rt) rt=New_Node();
        if(x<=l && r<=x){rt->v+=C;return;}
        int mid=(l+r)/;
        if(x<=mid) update1(rt->l,l,mid,x,C); else update1(rt->r,mid+,r,x,C);
        rt->v=gcd(rt->lv(),rt->rv());
    }
  inline void update2(Tnode *&rt,Tnode *&rtl,Tnode *&rtr,int l,int r,int x)
    {
        if(l>r || x<l || r<x) return;
        if(!rt) rt=New_Node();
        if(!rtl) rtl=New_Node();
        if(!rtr) rtr=New_Node();
        if(x<=l && r<=x){rt->v=gcd( rtl->v ,rtr->v ); return;}
        int mid=(l+r)/;
        if(x<=mid)update2(rt->l,rtl->l,rtr->l,l,mid,x);else update2(rt->r,rtl->r,rtr->r,mid+,r,x);
        rt->v=gcd(rt->lv(),rt->rv());
    }
  inline LL ask(Tnode *&rt,int l,int r,int x,int y)
    {
        if(l>r || x>y || r<x || y<l) return ;
        if(!rt) return ;
        if(x<=l && r<=y) return rt->v;
        int mid=(l+r)/;
        return gcd( ask(rt->l,l,mid,x,y) , ask(rt->r,mid+,r,x,y) );
    }

  inline LL ask(int rt,int l,int r,int x1,int y1,int x2,int y2)
    {
        if(l>r || x1>x2 || x2<l || r<x1) return ;
            if(x1<=l && r<=x2) return ask(root[rt],,M,y1,y2);
            int mid=(l+r)/;
            return gcd( ask(rt*,l,mid,x1,y1,x2,y2) , ask(rt*+,mid+,r,x1,y1,x2,y2) );
        }
  inline void update(int rt,int l,int r,int x,int y,LL C)
    {
        if(l>r || x<l || r<x)return;
            int mid=(l+r)/;
            if(l==r)
              update1(root[rt],,M,y,C);
            else
              {
                if(x<=mid)update(rt*,l,mid,x,y,C); else update(rt*+,mid+,r,x,y,C);
                    update2(root[rt],root[rt*],root[rt*+],,M,y);
                }
    }

  inline LL xunwen(int x,int y)
    {
        return ask(,,N,,,x,y);
    }
  inline void xiugai(PII t1,PII t2,LL C)
    {
        int x1=t1.fi,y1=t1.se,x2=t2.fi,y2=t2.se;
        if(x1>x2)swap(x1,x2);
        if(y1>y2)swap(y1,y2);
            update(,,N,x1,y1,C);
            if(x2+<=N)update(,,N,x2+,y1,-C);
        if(y2+<=M)update(,,N,x1,y2+,-C);
            if(x2+<=N && y2+<=M)update(,,N,x2+,y2+,C);
    }
}data[];

inline PII zhuan(int f,int i,int j)
  {
      switch(f)
        {
            case :return PII(j-Y+,X-i+);break;
            case :return PII(Y-j+,X-i+);break;
            case :return PII(Y-j+,i-X+);break;
            case :return PII(j-Y+,i-X+);break;
        }
  }

inline void build()
  {
      int i,j;
        data[].clear(M-Y+,X);
        re(i,,X)re(j,Y,M)data[].xiugai(zhuan(,i,j),zhuan(,i,j),mp[i][j]);
        data[].clear(Y,X);
        re(i,,X)re(j,,Y)data[].xiugai(zhuan(,i,j),zhuan(,i,j),mp[i][j]);
        data[].clear(Y,N-X+);
        re(i,X,N)re(j,,Y)data[].xiugai(zhuan(,i,j),zhuan(,i,j),mp[i][j]);
        data[].clear(M-Y+,N-X+);
        re(i,X,N)re(j,Y,M)data[].xiugai(zhuan(,i,j),zhuan(,i,j),mp[i][j]);
  }

int main()
  {
      freopen("chess.in","r",stdin);
      freopen("chess.out","w",stdout);
      int i,j;
      N=gint();M=gint();
      X=gint();Y=gint();
      T=gint();
      re(i,,N){mp[i].push_back();re(j,,M)mp[i].push_back(gll());mp[i].push_back();}
      re(j,,M+)mp[].push_back(),mp[N+].push_back();
      build();
      while(T--)
        {
            int f=gint(),x1=gint(),y1=gint(),x2=gint(),y2=gint();
            LL C,res;
            switch(f)
              {
                  case :
                      res=;
                      res=gcd(res,data[].xunwen(y2+,x1+));
                      res=gcd(res,data[].xunwen(y1+,x1+));
                      res=gcd(res,data[].xunwen(y1+,x2+));
                      res=gcd(res,data[].xunwen(y2+,x2+));
                      PF("%I64d\n",res);
                  break;
                  case :
                      C=gll();
                      if(x1<=X && y2>=Y) data[].xiugai( zhuan(,min(X,x2),max(Y,y1)) , zhuan(,x1,y2) , C );
                      if(x1<=X && y1<=Y) data[].xiugai( zhuan(,min(X,x2),min(Y,y2)) , zhuan(,x1,y1) , C );
                      if(x2>=X && y1<=Y) data[].xiugai( zhuan(,max(X,x1),min(Y,y2)) , zhuan(,x2,y1) , C );
                      if(x2>=X && y2>=Y) data[].xiugai( zhuan(,max(X,x1),max(Y,y1)) , zhuan(,x2,y2) , C );
                  break;
              }
        }
      return ;
  }