BZOJ 2752: [HAOI2012]高速公路(road)( 线段树 )

对于询问[L, R], 我们直接考虑每个p(L≤p≤R)的贡献，可以得到

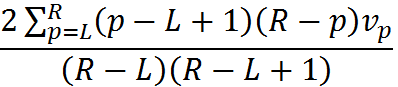
然后化简一下得到

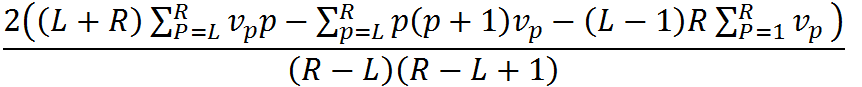
这样就可以很方便地用线段树, 维护一个p, p*v_p, p*(p+1)*v_p就可以了

--------------------------------------------------------------------

#include<cstdio>

#include<cstring>

#include<algorithm>

 

using namespace std;

 

typedef long long ll;

 

const int maxn = 100009;

 

int N, Q, L, R, v;

ll sump[maxn];

 

struct Node {

Node *l, *r;

int Ad;

ll v, pv, ppv;

Node() : Ad(0) {

}

void update(int _l, int _r) {

if(_l == _r) {

v += Ad;

Ad = 0;

pv = v * _l;

ppv = v * (sump[_r] - sump[_l - 1]);

} else {

v = l->v + r->v;

pv = l->pv + r->pv;

ppv = l->ppv + r->ppv;

if(Ad) {

v += ll(Ad) * (_r - _l + 1);

pv += ll(Ad) * (_l + _r) * (_r - _l + 1) >> 1;

ppv += ll(Ad) * (sump[_r] - sump[_l - 1]);

}

}

}

void pushDown() {

if(Ad != 0) {

l->Ad += Ad;

r->Ad += Ad;

Ad = 0;

}

}

} pool[maxn << 1], *Root, *pt = pool;

 

void Build(Node* t, int l, int r) {

int m = (l + r) >> 1;

if(l == r) return;

Build(t->l = pt++, l, m);

Build(t->r = pt++, m + 1, r);

}

 

void Modify(Node* t, int l, int r) {

if(L <= l && r <= R) {

t->Ad += v;

} else {

t->pushDown();

int m = (l + r) >> 1;

L <= m ? Modify(t->l, l, m) : t->l->update(l, m);

m < R ? Modify(t->r, m + 1, r) : t->r->update(m + 1, r);

}

t->update(l, r);

}

 

ll Query(Node* t, int l, int r) {

if(L <= l && r <= R)

return t->pv * (L + R) - t->ppv - t->v * R * (L - 1);

int m = (l + r) >> 1;

ll ret = 0;

t->pushDown();

t->l->update(l, m); t->r->update(m + 1, r);

if(L <= m) ret += Query(t->l, l, m);

if(m < R) ret += Query(t->r, m + 1, r);

return ret;

}

 

ll gcd(ll x, ll y) {

return y ? gcd(y, x % y) : x;

}

 

int main() {

scanf("%d%d", &N, &Q);

sump[0] = 0;

for(int i = 1; i <= N; i++)

sump[i] = ll(i) * (i + 1) + sump[i - 1];

Build(Root = pt++, 1, N);

while(Q--) {

char c;

scanf(" %c%d%d", &c, &L, &R);

if(c == 'Q') {

ll tot = Query(Root, 1, N), n = (ll) (R - L) * (R - L + 1) / 2;

ll d = gcd(tot, n);

printf("%lld/%lld\n", tot / d, n / d);

} else {

scanf("%d", &v);

R--;

Modify(Root, 1, N);

}

}

return 0;

}

--------------------------------------------------------------------

2752: [HAOI2012]高速公路(road)

Time Limit: 20 Sec  Memory Limit: 128 MB
Submit: 968  Solved: 339
[Submit][Status][Discuss]

Description

Y901高速公路是一条重要的交通纽带，政府部门建设初期的投入以及使用期间的养护费用都不低，因此政府在这条高速公路上设立了许多收费站。
Y901高速公路是一条由N-1段路以及N个收费站组成的东西向的链，我们按照由西向东的顺序将收费站依次编号为1~N，从收费站i行驶到i+1(或从i+1行驶到i)需要收取Vi的费用。高速路刚建成时所有的路段都是免费的。
政府部门根据实际情况，会不定期地对连续路段的收费标准进行调整，根据政策涨价或降价。
无聊的小A同学总喜欢研究一些稀奇古怪的问题，他开车在这条高速路上行驶时想到了这样一个问题:对于给定的l,r(l<r),在第l个到第r个收费站里等概率随机取出两个不同的收费站a和b，那么从a行驶到b将期望花费多少费用呢?

Input

第一行2个正整数N,M，表示有N个收费站，M次调整或询问
接下来M行，每行将出现以下两种形式中的一种
C l r v 表示将第l个收费站到第r个收费站之间的所有道路的通行费全部增加v
Q l r   表示对于给定的l,r，要求回答小A的问题
所有C与Q操作中保证1<=l<r<=N

Output

对于每次询问操作回答一行，输出一个既约分数
若答案为整数a，输出a/1

Sample Input

4 5
C 1 4 2
C 1 2 -1
Q 1 2
Q 2 4
Q 1 4

Sample Output

1/1
8/3
17/6

HINT

数据规模

所有C操作中的v的绝对值不超过10000

在任何时刻任意道路的费用均为不超过10000的非负整数

所有测试点的详细情况如下表所示

Test N M

1 =10 =10

2 =100 =100

3 =1000 =1000

4 =10000 =10000

5 =50000 =50000

6 =60000 =60000

7 =70000 =70000

8 =80000 =80000

9 =90000 =90000

10 =100000 =100000

Source