【并查集专题】【HDU】

PS：做到第四题才发现 2,3题的路径压缩等于没写

How Many Tables

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 14542    Accepted Submission(s): 7132

Problem Description

Today is Ignatius' birthday. He invites a lot of friends. Now it's dinner time. Ignatius wants to know how many tables he needs at least. You have to notice that not all the friends know each other, and all the friends do not want to stay with strangers.



One important rule for this problem is that if I tell you A knows B, and B knows C, that means A, B, C know each other, so they can stay in one table.



For example: If I tell you A knows B, B knows C, and D knows E, so A, B, C can stay in one table, and D, E have to stay in the other one. So Ignatius needs 2 tables at least.

 

Input

The input starts with an integer T(1<=T<=25) which indicate the number of test cases. Then T test cases follow. Each test case starts with two integers N and M(1<=N,M<=1000). N indicates the number of friends, the friends are marked from 1 to N. Then M lines
follow. Each line consists of two integers A and B(A!=B), that means friend A and friend B know each other. There will be a blank line between two cases.

 

Output

For each test case, just output how many tables Ignatius needs at least. Do NOT print any blanks.

 

Sample Input

2
5 3
1 2
2 3
4 5

5 1
2 5

 

Sample Output

2
4

 

Author

Ignatius.L

 

裸的并查集没什么好说的

#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <ctime>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <string>
#define oo 0x13131313
using namespace std;
int N,M;
int Set[1001];
int ans;
void YCL()
{
	ans=0;
	for(int i=0;i<=N;i++)
	Set[i]=i;
}
int find(int x)
{
	if(x!=Set[x])
	Set[x]=find(Set[x]);
	return Set[x];
}
int Union(int a,int b)
{
	int a1=find(a);
	int b1=find(b);
	if(a1!=b1)
	{
		Set[a1]=b1;
		return 1;
	}
	else return 0;
}
void input()
{
	cin>>N>>M;
	int a,b;
	YCL();
	for(int i=1;i<=M;i++)
	{
		cin>>a>>b;
		if(Union(a,b))
		ans++;
	}
}
int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		input();
		cout<<N-ans<<endl;
	}
	return 0;
}
  

小希的迷宫

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 27792    Accepted Submission(s): 8589

Problem Description

上次Gardon的迷宫城堡小希玩了很久（见Problem B），现在她也想设计一个迷宫让Gardon来走。但是她设计迷宫的思路不一样，首先她认为所有的通道都应该是双向连通的，就是说如果有一个通道连通了房间A和B，那么既可以通过它从房间A走到房间B，也可以通过它从房间B走到房间A，为了提高难度，小希希望任意两个房间有且仅有一条路径可以相通（除非走了回头路）。小希现在把她的设计图给你，让你帮忙判断她的设计图是否符合她的设计思路。比如下面的例子，前两个是符合条件的，但是最后一个却有两种方法从5到达8。 

 

Input

输入包含多组数据，每组数据是一个以0 0结尾的整数对列表，表示了一条通道连接的两个房间的编号。房间的编号至少为1，且不超过100000。每两组数据之间有一个空行。 

整个文件以两个-1结尾。

 

Output

对于输入的每一组数据，输出仅包括一行。如果该迷宫符合小希的思路，那么输出"Yes"，否则输出"No"。

 

Sample Input

6 8  5 3  5 2  6 4
5 6  0 0

8 1  7 3  6 2  8 9  7 5
7 4  7 8  7 6  0 0

3 8  6 8  6 4
5 3  5 6  5 2  0 0

-1 -1

 

Sample Output

Yes
Yes
No

 

Author

Gardon

 

Source

HDU 2006-4 Programming Contest

 

Recommend

lxj   |   We have carefully selected several similar problems for you:  1232 1856 1325 1233 1198 

 

几点注意：

1.不止要判环，还要判断是否是一棵树，而不是多棵树

2.注意0 0 //，1 1 0 0 这样的数据

3.编号非连续的,所以开个数组存编号

#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <ctime>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <string>
#define oo 0x13131313
using namespace std;
int father[100001];
int A[200001];
int Max=-1,tot=0;
int find(int x)
{
	if(x!=father[x])
	father[x]=find(father[x]);
	return father[x];
}
int Union(int a,int b)
{
	int a1=find(a);
	int a2=find(b);
	if(a1==a2) return 0;
	else father[a1]=a2;
	return 1;
}
void init()
{
	freopen("a.in","r",stdin);
	freopen("a.out","w",stdout);
}
void YCL()
{
	for(int i=1;i<=100000;i++)
	{
		father[i]=i;
	}
}
int main()
{
  // init();
	int a,b,OK=1;
	while(1)
	{
		YCL();
		OK=1;Max=-1;tot=0;
		while(cin>>a>>b)
		{
			if(a==-1&&b==-1) return 0;
			else if(a==0&&b==0) {break;}
			else if(OK)
			        if(Union(a,b)==0) OK=0;
			A[++tot]=a;
			A[++tot]=b;
		}
		if(OK==1) {
				  	for(int i=1;i<=tot;i++)
				  	    if(find(father[A[i]])!=find(father[A[1]])) OK=0;
				  	if(OK==1) printf("Yes\n");
				  	else printf("No\n");
				  }
		else cout<<"No"<<endl;
	}
	return 0;
}
  

Is It A Tree?

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 15095    Accepted Submission(s): 3342

Problem Description

A tree is a well-known data structure that is either empty (null, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties. 

There is exactly one node, called the root, to which no directed edges point. 



Every node except the root has exactly one edge pointing to it. 



There is a unique sequence of directed edges from the root to each node. 



For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.








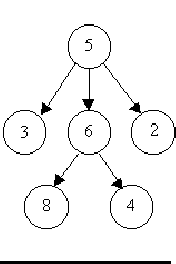
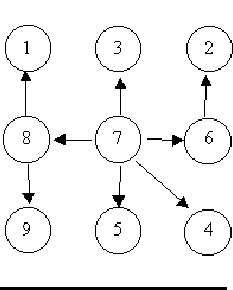
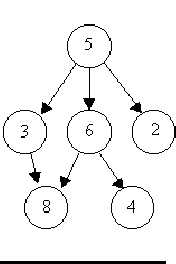
In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not. 

 

Input

The input will consist of a sequence of descriptions (test cases) followed by a pair of negative integers. Each test case will consist of a sequence of edge descriptions followed by a pair of zeroes Each edge description will consist of a pair of integers;
the first integer identifies the node from which the edge begins, and the second integer identifies the node to which the edge is directed. Node numbers will always be greater than zero. 

 

Output

For each test case display the line ``Case k is a tree." or the line ``Case k is not a tree.", where k corresponds to the test case number (they are sequentially numbered starting with 1). 

 

Sample Input

6 8 5 3 5 2 6 4
5 6 0 0
8 1 7 3 6 2 8 9 7 5
7 4 7 8 7 6 0 0
3 8 6 8 6 4
5 3 5 6 5 2 0 0
-1 -1

 

Sample Output

Case 1 is a tree.
Case 2 is a tree.
Case 3 is not a tree.

 

Source

North Central North America 1997

 

注意 这和上面的题有点不一样 是一个有向图

所以要判断入度

否则会出现

判断成树的情况

代码如下：

#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <ctime>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <string>
#define oo 0x13131313
using namespace std;
int father[100001];
int A[200001];
int T[200001];
int Max=-1,tot=0;
int find(int x)
{
	if(x!=father[x])
	father[x]=find(father[x]);
	return father[x];
}
int Union(int a,int b)
{
	int a1=find(a);
	int a2=find(b);
	if(a1==a2) return 0;
	else father[a1]=a2;
	return 1;
}
void init()
{
	freopen("a.in","r",stdin);
	freopen("a.out","w",stdout);
}
void YCL()
{
	for(int i=1;i<=tot;i++)
	{
		father[A[i]]=A[i];
		T[A[i]]=0;
	}
}
int main()
{
  // init();
	int a,b,OK=1;
	int kk=0;
	while(1)
	{
		kk++;
		OK=1;Max=-1;tot=0;
		while(cin>>a>>b)
		{
			if(a<0||b<0) return 0;
			else if(a==0&&b==0) {break;}
			A[++tot]=a;
			A[++tot]=b;
		}
		YCL();
		for(int i=1;i<=tot/2;i++)
		{
				if(OK)
			        {
			        	if(Union(A[2*(i-1)+1],A[2*i])==0) OK=0;
			    		T[A[2*i]]++;
					}
		}
		if(OK==1) {
				  	for(int i=1;i<=tot;i++)
				  	   {
				  	   	 if(find(father[A[i]])!=find(father[A[1]])) OK=0;
				  		 if(T[A[i]]>1) OK=0;
					   }
				  	if(OK==1) printf("Case %d is a tree.\n",kk);
				  	else printf("Case %d is not a tree.\n",kk);
				  }
		else printf("Case %d is not a tree.\n",kk);
	}
	return 0;
}
  

More is better

Time Limit: 5000/1000 MS (Java/Others)    Memory Limit: 327680/102400 K (Java/Others)

Total Submission(s): 15588    Accepted Submission(s): 5737

Problem Description

Mr Wang wants some boys to help him with a project. Because the project is rather complex, the more boys come, the better it will be. Of course there are certain requirements.



Mr Wang selected a room big enough to hold the boys. The boy who are not been chosen has to leave the room immediately. There are 10000000 boys in the room numbered from 1 to 10000000 at the very beginning. After Mr Wang's selection any two of them who are
still in this room should be friends (direct or indirect), or there is only one boy left. Given all the direct friend-pairs, you should decide the best way.

 

Input

The first line of the input contains an integer n (0 ≤ n ≤ 100 000) - the number of direct friend-pairs. The following n lines each contains a pair of numbers A and B separated by a single space that suggests A and B are direct friends. (A ≠ B, 1 ≤ A, B ≤ 10000000)

 

Output

The output in one line contains exactly one integer equals to the maximum number of boys Mr Wang may keep. 

 

Sample Input

4
1 2
3 4
5 6
1 6
4
1 2
3 4
5 6
7 8

 

Sample Output

4
2

Hint

A and B are friends(direct or indirect), B and C are friends(direct or indirect),
then A and C are also friends(indirect).

 In the first sample {1,2,5,6} is the result.
In the second sample {1,2},{3,4},{5,6},{7,8} are four kinds of answers.
 

 

Author

lxlcrystal@TJU

 

Source

HDU 2007 Programming Contest - Final

 

Recommend

lcy   |   We have carefully selected several similar problems for you:  1232 1879 1863 1875 1102 

 

MAP离散化+路径压缩。。 还一直以为是MAP导致TLE 结果发现是2,3题的路径压缩写错了。。

#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <ctime>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <string>
#include<map>
#define oo 0x13131313
using namespace std;
int N;
int father[200000];
int A[200000];
int B[200000];
int num[200000];
map<int,int> Hash;
int tot=0;
int ans=1;
void input()
{
	Hash.clear();
	tot=0;ans=1;
	int a,b;
	for(int i=1;i<=N;i++)
	{
		scanf("%d%d",&a,&b);
		B[(2*i-1)]=A[(2*i-1)]=a;
		B[(2*i)]=A[(2*i)]=b;
	}
}
void CSH()
{
	B[0]=-1;
	sort(B+1,B+2*N+1);
	for(int i=1;i<=2*N;i++)
	{
		if(B[i]!=B[i-1])
		Hash[B[i]]=++tot;
	}
	for(int i=1;i<=tot;i++)
	{
		father[i]=i;
		num[i]=1;
	}
}
int find(int x)
{
	if(x!=father[x])
	father[x]=find(father[x]);
	return father[x];
}
int Union(int a,int b)
{
	int a1=find(a);
	int b1=find(b);
	if(a1==b1) return 0;
	else
	{
		father[a1]=b1;
		num[b1]+=num[a1];
		if(num[b1]>ans) ans=num[b1];
	}
	return 1;
}
void solve()
{
	for(int i=1;i<=N;i++)
	{
		Union(Hash[A[(2*i-1)]],Hash[A[(2*i)]]);
	}
}
void init()
{
	freopen("a.in","r",stdin);
	freopen("a.out","w",stdout);
}
int main()
{
//	init();
	while(scanf("%d",&N)!=EOF)
	{
		input();
		CSH();
		solve();
		printf("%d\n",ans);
	}
	return 0;
}
  

Constructing Roads

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 14672    Accepted Submission(s): 5572

Problem Description

There are N villages, which are numbered from 1 to N, and you should build some roads such that every two villages can connect to each other. We say two village A and B are connected, if and only if there is a road between A and B, or there exists a village
C such that there is a road between A and C, and C and B are connected. 



We know that there are already some roads between some villages and your job is the build some roads such that all the villages are connect and the length of all the roads built is minimum.

 

Input

The first line is an integer N (3 <= N <= 100), which is the number of villages. Then come N lines, the i-th of which contains N integers, and the j-th of these N integers is the distance (the distance should be an integer within [1, 1000]) between village
i and village j.



Then there is an integer Q (0 <= Q <= N * (N + 1) / 2). Then come Q lines, each line contains two integers a and b (1 <= a < b <= N), which means the road between village a and village b has been built.

 

Output

You should output a line contains an integer, which is the length of all the roads to be built such that all the villages are connected, and this value is minimum. 

 

Sample Input

3
0 990 692
990 0 179
692 179 0
1
1 2

 

Sample Output

179

 

Source

kicc

 

Recommend

Eddy   |   We have carefully selected several similar problems for you:  1233 1301 1162 1232 1875 

 

给定N条建好路径的最小生成树

1.建好的路径就是权值为0即可，或直接克鲁斯卡尔

附代码：

#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <ctime>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <string>
#define oo 0x13131313
using namespace std;
struct edge
{
	int s,t,w;
};
int father[101];
edge A[20111];
int map[101][101];
int N;
int ans;
int tot=0;
int Q;
int k;
int cmp(const void *i,const void *j)
{
	edge *ii=(edge *)i;edge *jj=(edge *)j;
	return ii->w-jj->w;
}
void YCL()
{
	for(int i=1;i<=101;i++)
	{
		father[i]=i;
	}
}
int find(int x)
{
	if(x!=father[x])
	father[x]=find(father[x]);
	return father[x];
}
int Union(int a,int b)
{
	int a1=find(a);
	int b1=find(b);
	if(a1==b1) return 0;
	else
	{
		father[b1]=a1;
	}
	return 1;
}
void input()
{
	YCL();
	int temp,a,b;
	ans=0;
	tot=0;
	k=0;
	for(int i=1;i<=N;i++)
	 for(int j=1;j<=N;j++)
	 {
	 	scanf("%d",&map[i][j]);
		if(i<j)
		{
			tot++;
			A[tot].s=i;A[tot].t=j;A[tot].w=map[i][j];
		}
	}
	cin>>Q;
	for(int i=1;i<=Q;i++)
	{
		scanf("%d%d",&a,&b);
		if(Union(a,b))
		{
			k++;
		}
	}
}
void solve()
{
	int j=1;
	qsort(A+1,tot,sizeof(A[1]),cmp);
	for(int i=1;i<=N-1-k;i++)
	{
		while(Union(A[j].s,A[j].t)==0&&j<=tot)
		j++;
		ans+=A[j].w;
	}
}
int main()
{
	while(cin>>N)
	{
		input();
		solve();
		cout<<ans<<endl;
	}
}
  

后面还有几道生成树水题就不上了。。