leetcode-52-N皇后②
题目描述:

方法一:回溯
class Solution:
def totalNQueens(self, n: int) -> int:
def backtrack(i,tmp,col,z_diagonal,i_diagonal):
if i == n:
nonlocal res
res += 1
return
for j in range(n):
if j not in col and i+j not in z_diagonal and i-j not in i_diagonal:
backtrack(i+1,tmp+[s[:j]+"Q"+s[j+1:]],col|{j},z_diagonal|{i+j},i_diagonal|{i-j})
s = "." * n
res = 0
backtrack(0,[],set(),set(),set())
return res
另:位运算优化:*
class Solution:
def totalNQueens(self, n: int) -> int:
def backtrack(row = 0, hills = 0, next_row = 0, dales = 0, count = 0):
"""
:type row: 当前放置皇后的行号
:type hills: 主对角线占据情况 [1 = 被占据,0 = 未被占据]
:type next_row: 下一行被占据的情况 [1 = 被占据,0 = 未被占据]
:type dales: 次对角线占据情况 [1 = 被占据,0 = 未被占据]
:rtype: 所有可行解的个数
"""
if row == n: # 如果已经放置了 n 个皇后
count += 1 # 累加可行解
else:
# 当前行可用的列
# ! 表示 0 和 1 的含义对于变量 hills, next_row and dales的含义是相反的
# [1 = 未被占据,0 = 被占据]
free_columns = columns & ~(hills | next_row | dales) # 找到可以放置下一个皇后的列
while free_columns:
# free_columns 的第一个为 '1' 的位
# 在该列我们放置当前皇后
curr_column = - free_columns & free_columns # 放置皇后
# 并且排除对应的列
free_columns ^= curr_column count = backtrack(row + 1,
(hills | curr_column) << 1,
next_row | curr_column,
(dales | curr_column) >> 1,
count)
return count # 棋盘所有的列都可放置,
# 即,按位表示为 n 个 '1'
# bin(cols) = 0b1111 (n = 4), bin(cols) = 0b111 (n = 3)
# [1 = 可放置]
columns = (1 << n) - 1
return backtrack()
另:
class Solution:
def totalNQueens(self, n: int) -> int:
def DFS(n: int, row: int, cols: int, left: int, right: int):
""" 深度优先搜索
:param n: N皇后个数
:param row: 递归的深度
:param cols: 可被攻击的列
:param left: 左侧斜线上可被攻击的列
:param right: 右侧斜线上可被攻击的列
"""
if row >= n:
self.res += 1
return # 获取当前可用的空间
bits = (~(cols | left | right)) & ((1 << n) - 1) # 遍历可用空间
while bits:
# 获取一个位置
p = bits & -bits
DFS(n, row + 1, cols | p, (left | p) << 1, (right | p) >> 1)
bits = bits & (bits - 1) if not (n == 1 or n >= 4):
# N皇后问题只有在 N 大于等于 4 或等于 1 的时候才有解
return 0
self.res = 0
DFS(n, 0, 0, 0, 0)
return self.res
leetcode-52-N皇后②的更多相关文章
- Java实现 LeetCode 52 N皇后 II
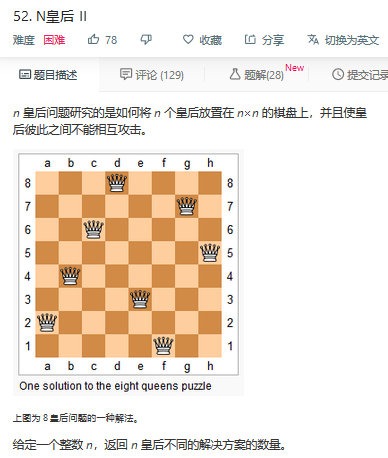
52. N皇后 II n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击. 上图为 8 皇后问题的一种解法. 给定一个整数 n,返回 n 皇后不同的解决方案 ...
- [LeetCode] 52. N皇后 II
题目链接 : https://leetcode-cn.com/problems/n-queens-ii/ 题目描述: n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间 ...
- leetcode 52 N皇后问题 II
51的简化版,省去根据排列话棋盘的工作,直接计数,代码: class Solution { public: int totalNQueens(int n) { ; vector<); dfs(n ...
- Leetcode之回溯法专题-52. N皇后 II(N-Queens II)
Leetcode之回溯法专题-52. N皇后 II(N-Queens II) 与51题的代码80%一样,只不过52要求解的数量,51求具体解,点击进入51 class Solution { int a ...
- leetcode 51. N皇后 及 52.N皇后 II
51. N皇后 问题描述 n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击. 上图为 8 皇后问题的一种解法. 给定一个整数 n,返回所有不同的 n 皇后 ...
- [LeetCode] 52. N-Queens II N皇后问题之二
The n-queens puzzle is the problem of placing nqueens on an n×n chessboard such that no two queens a ...
- [LeetCode] 52. N-Queens II N皇后问题 II
The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens ...
- [leetcode]52. N-Queens II N皇后
The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens ...
- [LeetCode] N-Queens N皇后问题
The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens ...
- LeetCode - 52. N-Queens II
52. N-Queens II Problem's Link --------------------------------------------------------------------- ...
随机推荐
- socket中的绑定
- C++使用cout输出中文,打印出来是乱码
windows下的控制台使用的是gbk编码.你输出的是unicode.在Vs中更改高级保存选项,将Unicode改为GB类型(比如GB18030)
- Java刷题笔记
能用StringBuffer的时候坚决不要用String,因为前者的时间和空间效率都更高. 牛顿法求平方根:随便找一个K,然后不断让 k=(k+x/k)/2;直到K的平方与x之间的差距小于限定值. 斐 ...
- ajax验证用户名是否存在,手机号是不是匹配
<label class="col-sm-2 control-label font">用户名</label> <div class="col ...
- Java中遍历数组的三种方式复习
1 for循环遍历 通常遍历数组都是使用for循环来实现.遍历一维数组很简单,遍历二维数组需要使用双层for循环,通过数组的length属性可获得数组的长度. 程序示例: package captai ...
- 【LeetCode 24】两两交换链表中的节点
题目链接 [题解] 简单的链表操作 [代码] /** * Definition for singly-linked list. * struct ListNode { * int val; * Lis ...
- 调用JavaScript实现字符串计算器
调用JavaScript实现字符串计算器 如果表达式是字符串的形式,那么一般我们求值都会遇到很大的问题. 这里有一种直接调用JavaScript的方法来返回数值,无疑神器. 代码如下: @Fros ...
- 单调栈+线段树——cf1220F
首先考虑初始排列,pi会让周围所有比其大的元素深度+1,所以要求每个点的深度,只要其被覆盖了几次即可 这个覆盖可以通过处理每个元素的左右边界(单调栈O(n))+线段树区间更新(Ologn(n))来做 ...
- 使用并行ssh提高工作效率
我们经常需要ssh到多个主机上执行相同的命令,为了提高效率,我们通常会自己写个脚本,循环遍历执行我们的命令,比如: for host in `cat hosts.txt`;do ssh usernam ...
- 剑指offer第二版面试题11:旋转数组的最小数字(JAVA版)
题目:把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转.输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素.例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数 ...
